11 因子分析
11.1 概要
このページでは探索的因子分析の方法を解説します。(探索的)因子分析とは、観察されたデータ(変数間の相関関係)から、直接は観察できない潜在変数(因子と呼ばれます)を見出す方法です。質問紙などから得られたデータをもとに、その質問紙が測定していると考えられる構成概念を抽出することなどによく使われます。
11.2 パッケージとデータセット
R で因子分析をする際は psych パッケージを使います。
因子の回転に使う GPArotation パッケージもついでにインストールしておきましょう。
psych パッケージには分析用のサンプルデータも入っています。
その中の bfi というデータをこの記事では用いることにします。
11.3 bfi データについて
国際パーソナリティ項目プール(International Personality Item Pool ipip.ori.org)で提供されている、パーソナリティの5因子モデル(IPIP-NEO)についての質問紙への回答(2800人分)のデータです。
dim( bfi )
## [1] 2800 28
head( bfi, 3 )
## A1 A2 A3 A4 A5 C1 C2 C3 C4 C5 E1 E2 E3 E4 E5 N1 N2 N3 N4 N5 O1 O2 O3 O4
## 61617 2 4 3 4 4 2 3 3 4 4 3 3 3 4 4 3 4 2 2 3 3 6 3 4
## 61618 2 4 5 2 5 5 4 4 3 4 1 1 6 4 3 3 3 3 5 5 4 2 4 3
## 61620 5 4 5 4 4 4 5 4 2 5 2 4 4 4 5 4 5 4 2 3 4 2 5 5
## O5 gender education age
## 61617 3 1 NA 16
## 61618 3 2 NA 18
## 61620 2 2 NA 172800行、28列のデータフレームです。
28列のうち、最初の25列が質問文への回答(6段階評定)です。最後の3列はそれぞれ
- 性別(1=男, 2=女)
- 学歴(1=高校入学, 2=高校卒業, 3=大学入学, 4=大学卒業, 5=大学院卒業)
- 年齢
です。
5因子それぞれにつき5問ずつで25個の質問文があります。
- Agreeableness(協調性・調和性):A1からA5
- Conscientiousness(勤勉性・誠実性):C1からC5
- Extraversion(外向性):E1からE5
- Neuroticism(神経症傾向・情緒不安定性):N1からN5
- Openness(開放性・経験への開放性):O1からO5
となっています。
具体的な各質問文は help(bfi) と打ってヘルプを表示させると確認できます。
今回の分析では性別・学歴・年齢は無視しますので、最初の25列だけを取り出したデータを作成し、以降はそれを用いて作業を進めます。
11.4 探索的因子分析について
因子分析は、例えば質問項目に対する回答データをもとに、各質問項目がどのような因子(心理学的構成概念など)を測定しているのかを調べることができる方法です。
因子分析には探索的因子分析と確認的因子分析があります。確認的因子分析では、因子の数や、どの項目がどの因子と関連しているかについて事前に仮説があり、それを検証するときに利用されます。探索的因子分析では、因子に関する明確な仮説がないときに利用されます。
探索的因子分析は次の手順で進みます。
- 因子数の決定
- 因子負荷の推定
- 因子軸の回転
- 因子の解釈
11.5 因子分析の前に
データが因子分析を用いるのに適切であるか(データに意味のある因子が発見できそうであるか)を判断するための基準として Kaiser-Meyer-Olkinの標本妥当性の測度(KMO 測度)があります。KMO 測度(KMO 指標)はデータの偏相関係数の情報を使って、データに少なくとも1つの潜在因子が存在しそうかを調べます(偏相関係数の2乗和がゼロに近いほどその可能性が高いことを利用します)。
KMO 指標は psych パッケージの KMO() 関数を使って計算できます。
KMO( dat )
## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = dat)
## Overall MSA = 0.85
## MSA for each item =
## A1 A2 A3 A4 A5 C1 C2 C3 C4 C5 E1 E2 E3 E4 E5 N1
## 0.74 0.84 0.87 0.87 0.90 0.83 0.79 0.85 0.82 0.86 0.83 0.88 0.89 0.87 0.89 0.78
## N2 N3 N4 N5 O1 O2 O3 O4 O5
## 0.78 0.86 0.88 0.86 0.85 0.78 0.84 0.76 0.76結果には全体指標(Overall MSA)と個別指標(MSA for each item)が表示されます。因子分析を使うには全体指標の値が 0.6 以上であることが望ましいとされます。もし全体指標の値が小さい場合には、個別指標の値が小さな変数を取り除くなどの対応を取ります。
今回のデータの場合は全体指標の値が 0.85 であるので因子分析をして問題はないと確認できました。
11.6 因子数の決定
探索的因子分析では因子の数をはじめに決定します。
bfi データの場合、これは5因子のパーソナリティモデルの質問紙ですので、因子の数はおそらくは 5 であると考えられます。因子数について仮説や想定がある状況では確認的因子分析をするのがより自然かもしれません。このページでは探索的因子分析の方法の説明のため、因子の数について仮説が無いふりをして分析を進めることにします。
11.6.1 古典的な方法
因子の固有値をプロットした折れ線グラフ(スクリープロットと呼ばれます)を参考に因子数を判断します。固有値とは因子の影響力の強さを示す値で、固有値の大きな因子を選ぶ(それ以外を捨てる)ことで因子数(選ばれた因子の数)を決定します。
# スクリープロットを描く
correlation = cor( dat, use = "complete.obs" ) # 相関行列を計算
fa.parallel( correlation, n.obs = 2436, fa = "fa" ) # スクリープロットを表示
abline( h = 0 ) # y = 0 の横線を追加
# Parallel analysis suggests that the number of factors = 6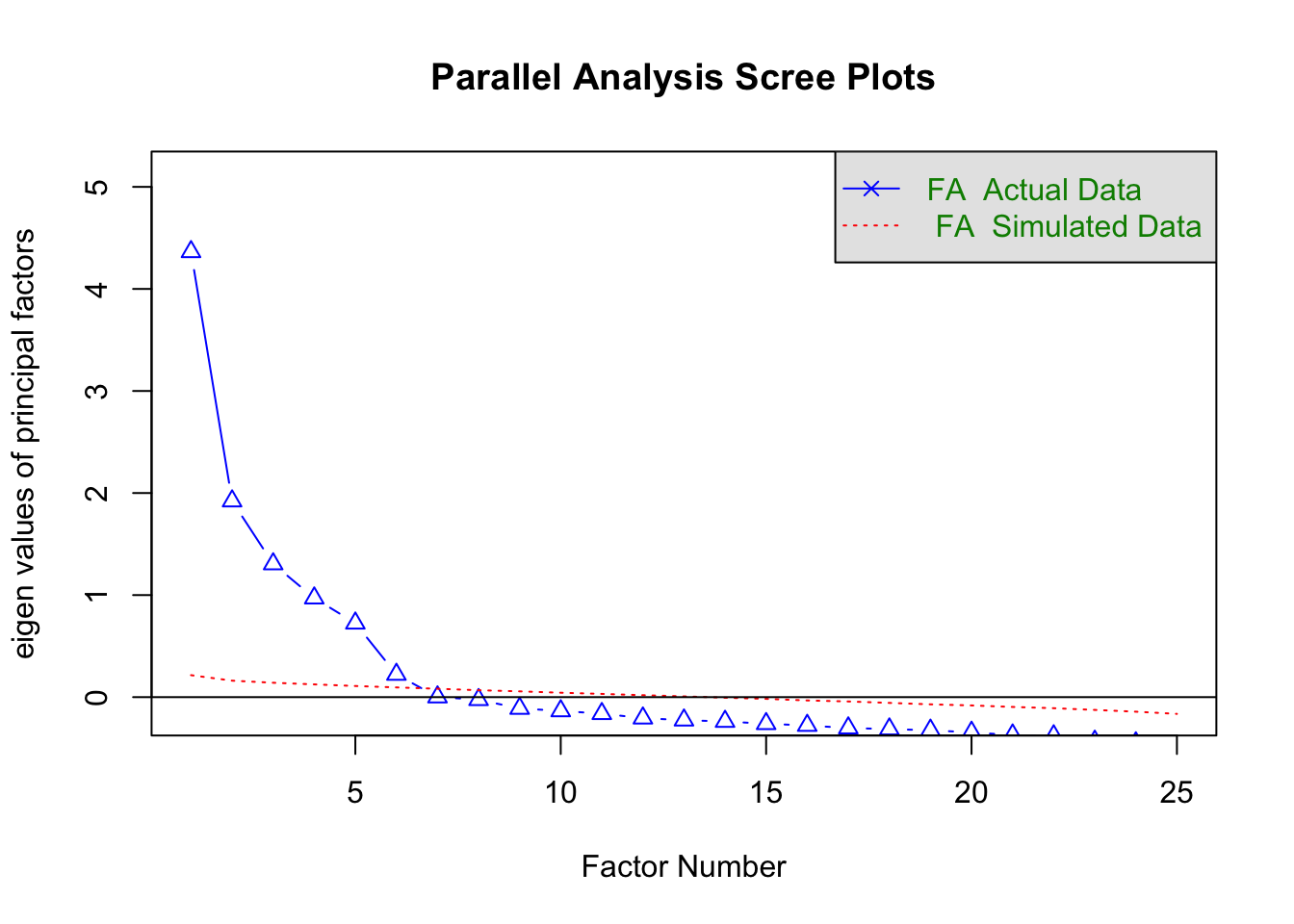
fa.parallel() 関数の第一引数には相関行列を入れ、n.obs はデータの数、fa は因子分析の場合は “fa” にします(主成分分析をする場合は “pc” とします)。
cor() 関数の use = "complete.obs" の部分は欠損値の扱いに関する指定です。今回のデータには NA が所々に含まれています(例えば dat[ 9, ] を見てみて下さい)。そこでこの指定方法では、各行について、25列のうちひとつでも NA を含むような行は除外して相関係数を計算させています。NA を含む場合の相関係数の計算に関しては以下のページが参考になります。
http://keita43a.hatenablog.com/entry/2018/04/10/034230
fa.parallel() 関数の n.obs の値に本来のデータ数である 2800 ではなく 2436 というよく分からない数字を指定している理由ですが、相関係数の計算の際に NA を含む行を除外したために、データの数が 2436 へと減ったからです。2436 という数字は dim( na.omit( dat ) ) または dim( dat[ complete.cases( dat ), ] ) とすれば分かります。もしくは sum( complete.cases( dat ) ) としても 2436 という数が得られます。
上記の方法では相関行列を求めたりデータの数を調べたりと色々とややこしくて面倒です。単純に、元データを引数に入れて次のように書くことも可能です。
# スクリープロットを描く
fa.parallel( dat, fa = "fa", use = "complete.obs" ) # スクリープロットを表示
abline( h = 0 ) # y = 0 の横線を追加
# Parallel analysis suggests that the number of factors = 6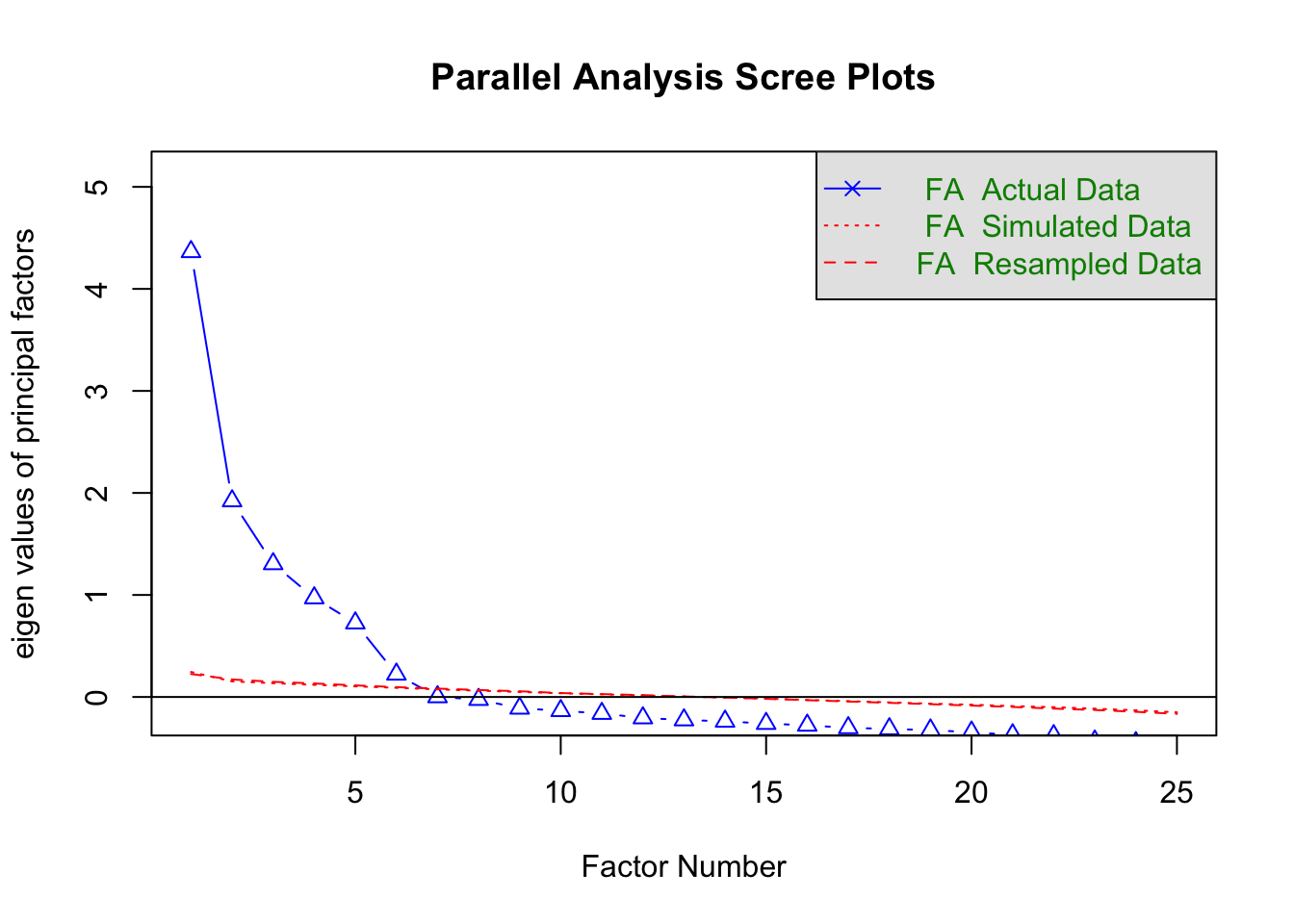
この図の青線は、各要因の固有値を折れ線グラフにしたものです。赤い点線(Simulated Data)は乱数データに因子分析をした結果、赤い破線(Resampled Data)は実データをランダムに並べ替えたデータに対して因子分析をした結果です(2種類の赤線はほぼ同じ結果であるため、重なって区別がつかなくなっています)。
大きな固有値を持つ因子の選択基準がいくつかあります。
- カイザー・ガットマン(Kaiser-Guttman)基準:固有値の値が0以上(因子分析の場合)または1以上(主成分分析の場合)の因子を選択する
- スクリーテスト(Cattell Scree test):グラフの線が強く折れ曲がった位置までの因子を選択
- 平行分析(parallel analysis):ランダムに生成したデータの固有値よりも大きな固有値を持つ因子を選択
カイザー基準の場合、7番目の因子までが固有値が0以上なので、因子数は 7 と判断されます。
スクリーテストの場合、2番目や7番目の因子の位置でグラフの折れ曲がりが強いので、2 や 7 が因子数と判断できます。基準があいまいなので他の判断基準と合わせて考える必要があります。
平行分析では、固有値が赤線を上回る因子を選びます。因子番号 6 までは図の青線は赤線より上にありますが、7 以降は青線の方が下になっているので、因子数は 6 と判断されます。fa.parallel() 関数を実行した際には平行分析の結果が文章で表示されます(# Parallel analysis suggests that the number of factors = 6)。
カイザー基準で判断する場合、因子の固有値が 0 に近いと固有値の値をグラフから読み取るのが難しくなります。その場合は fa.parallel( dat, plot = F )$fa.values とすれば固有値の値が表示できます。
11.6.2 より客観的な基準
因子数の決定の統計的な基準として、MAP 基準や BIC 基準などがあります。
# MAP/BIC 基準の因子数の計算
VSS( dat, n = 8 )
# 略
# The Velicer MAP achieves a minimum of 0.01 with 5 factors
# BIC achieves a minimum of -513.09 with 8 factors
# 略VSS() 関数を実行すると結果が色々と表示されますが、上に抜き出した箇所が MAP 基準 と BIC 基準 の結果です。MAP 基準では因子数 5、BIC 基準では因子数 8 が提案されています。
MAP 基準は少なめの因子数を、BIC 基準や平行分析は多めの因子数を提案する性質があります。
11.6.3 最終的な判断
因子数を決定する唯一の基準はなく、複数の基準を考慮して総合的に決めることになります。平行分析や MAP/BIC 基準を利用することが現在は推奨されており、カイザー基準やスクリーテストにはあまり頼らない方が良いと考えられます。また、データに基づくこれらの基準だけではなく、因子の解釈可能性や理論的背景なども考慮した上で因子数を決めることが重要です。
今回の場合、少なくとも 5 因子(MAP 基準)、多くても 8 因子(BIC 基準)にするべきだとデータに基づいて提案されており、また質問紙が 5 因子のパーソナリティ質問紙であることを考えて、因子数は 5 にすることに決定します。
因子数の決定に関しては以下のスライド資料も参考にして下さい。
https://www.slideshare.net/simizu706/r-42283141
11.7 因子負荷の推定
因子数が決まったので、fa() 関数で因子分析を行います。
25個の各質問項目が 5 つの因子それぞれをどの程度反映しているか(因子負荷)を計算します。
# 因子負荷の推定
result = fa( dat, nfactors = 5, fm = "minres", rotate = "oblimin", use = "complete.obs" )
print( result, digits = 3, sort = T )nfactors は因子数で、5 を指定しています。
fm は因子負荷の推定法で、“minres”(最小残差法、デフォルト)や “ml”(最尤法)などの選択肢があります。
rotate は因子軸の回転方法(後述)です。ここではオブリミン回転を指定しています。
use は相関行列を計算する際の欠損値の扱い(Notes で前述)です。
結果を print() 関数で表示させていますが、オプションで表示桁数を小数第3位までとし、また表示順をソートさせることで結果を見やすくしています。
因子負荷の推定結果は次のようになっています。
# Standardized loadings (pattern matrix) based upon correlation matrix
# item MR2 MR1 MR3 MR5 MR4 h2 u2 com
# N1 16 0.836 0.206 0.023 -0.248 -0.103 0.681 0.319 1.34
# N2 17 0.791 0.135 0.039 -0.218 -0.026 0.608 0.392 1.22
# N3 18 0.741 0.012 0.001 -0.022 -0.022 0.544 0.456 1.00
# N4 19 0.533 -0.311 -0.090 0.074 0.087 0.506 0.494 1.79
# N5 20 0.529 -0.139 0.039 0.139 -0.170 0.349 0.651 1.52
# E2 12 0.143 -0.711 0.045 0.013 0.000 0.546 0.454 1.09
# E4 14 -0.019 0.660 -0.033 0.202 -0.135 0.541 0.459 1.28
# E1 11 -0.034 -0.636 0.159 -0.007 -0.027 0.348 0.652 1.13
# E3 13 0.093 0.545 -0.049 0.156 0.233 0.441 0.559 1.63
# E5 15 0.138 0.498 0.229 -0.034 0.157 0.407 0.593 1.83
# C2 7 0.162 -0.090 0.697 0.040 0.048 0.454 0.546 1.16
# C4 9 0.173 0.070 -0.652 0.029 -0.057 0.477 0.523 1.18
# C3 8 0.030 -0.092 0.597 0.066 -0.063 0.324 0.676 1.10
# C1 6 0.073 -0.030 0.567 -0.028 0.159 0.348 0.652 1.20
# C5 10 0.209 -0.069 -0.561 0.026 0.089 0.435 0.565 1.37
# A3 3 0.037 0.236 0.010 0.621 -0.015 0.540 0.460 1.29
# A2 2 0.046 0.118 0.065 0.611 -0.005 0.463 0.537 1.11
# A5 5 -0.085 0.331 -0.031 0.489 0.007 0.470 0.530 1.84
# A1 1 0.149 0.123 0.064 -0.462 -0.058 0.204 0.796 1.44
# A4 4 -0.027 0.120 0.188 0.411 -0.174 0.302 0.698 2.02
# O3 23 0.052 0.299 -0.031 0.045 0.577 0.475 0.525 1.54
# O5 25 0.105 0.034 -0.014 0.017 -0.543 0.296 0.704 1.09
# O1 21 0.018 0.193 0.039 -0.005 0.491 0.317 0.683 1.32
# O2 22 0.188 0.043 -0.061 0.112 -0.484 0.267 0.733 1.47
# O4 24 0.171 -0.232 -0.013 0.184 0.370 0.246 0.754 2.73MR1 の列は第1因子の因子負荷、MR2 の列は第2因子の因子負荷、となっています。
因子負荷は因子と各項目との関連の強さで、1 から -1 の範囲の値です。数値(の絶対値)が大きいほど強い関連を意味します。例えば、MR2(第2因子)は N1〜N5と関連が強いことがわかります。
h2 の列は共通性、u2 の列は独自性を示します。
共通性とは観測変数(項目)の平方和のうち、共通因子で説明できる部分の割合で、独自性は「1 - 共通性」で得られる値です。共通性が 0.3 よりも低い項目は因子分析から除外した方がいいかもしれない項目です。
# MR2 MR1 MR3 MR5 MR4
# SS loadings 2.692 2.587 2.019 1.794 1.497
# Proportion Var 0.108 0.103 0.081 0.072 0.060
# Cumulative Var 0.108 0.211 0.292 0.364 0.424
# Proportion Explained 0.254 0.244 0.191 0.169 0.141
# Cumulative Proportion 0.254 0.499 0.689 0.859 1.000- SS loadings: 因子寄与。因子負荷の2乗和で、その因子が説明できる観測変数の分散の大きさ。
- Proportion Var: 因子寄与率。因子寄与を項目数(ここでは25)で割った値。
- Cumulative Var: 累積寄与率。因子寄与率の累積合計。
- Proportion Explained: 説明率。
- Cumulative Proportion: 累積説明率。
# With factor correlations of
# MR2 MR1 MR3 MR5 MR4
# MR2 1.000 -0.256 -0.224 -0.013 0.040
# MR1 -0.256 1.000 0.399 0.345 0.142
# MR3 -0.224 0.399 1.000 0.236 0.192
# MR5 -0.013 0.345 0.236 1.000 0.155
# MR4 0.040 0.142 0.192 0.155 1.000ここは因子間の相関係数が表示されています。
11.7.1 因子負荷の可視化
fa.diagram() 関数を使って図の作成ができます。
result = fa( dat, nfactors = 5, fm = "minres", rotate = "oblimin", use = "complete.obs" )
fa.diagram( result )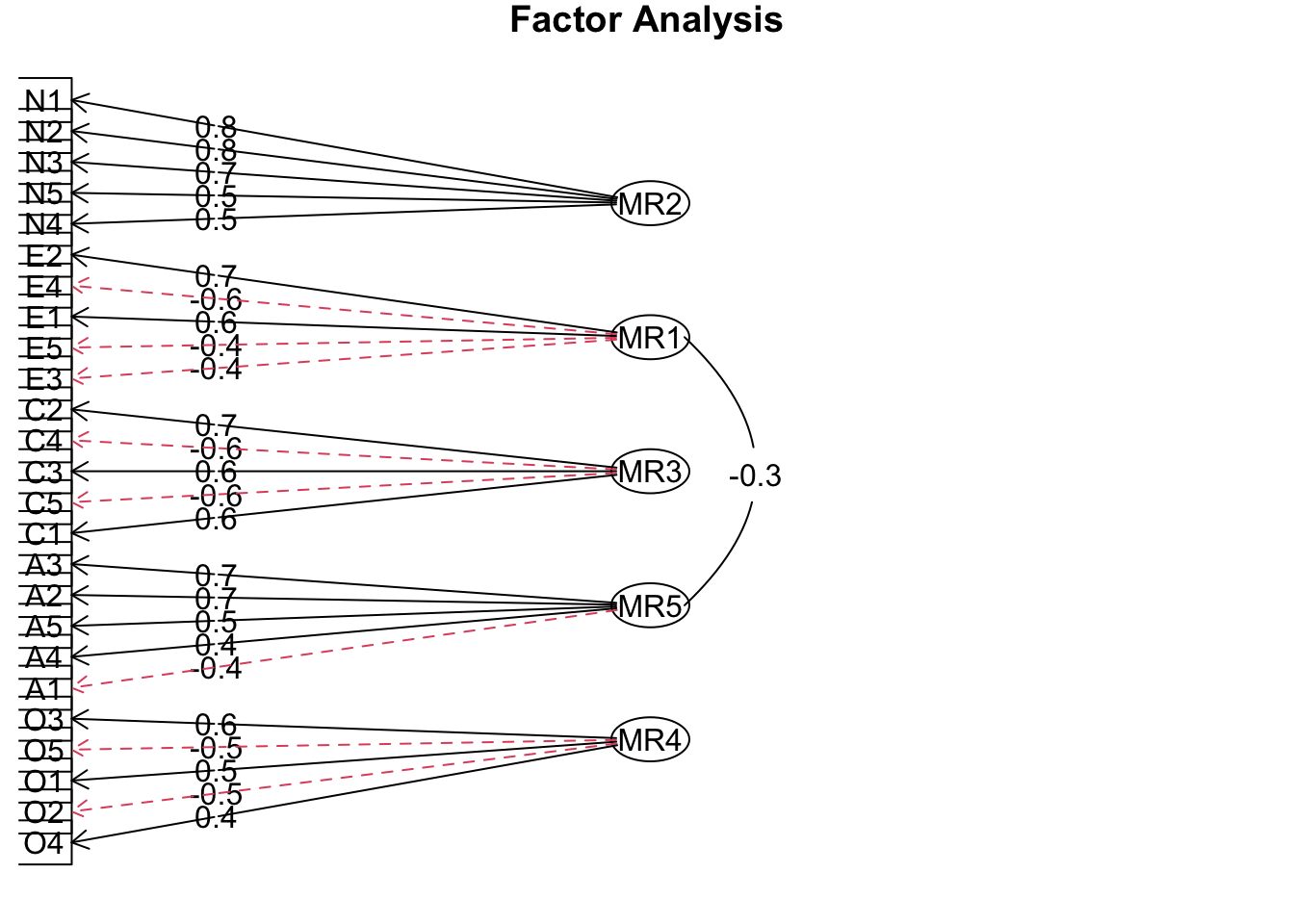
各因子がどの変数と関連しているかが視覚的に確認できます。
11.7.2 因子負荷の表示
因子負荷の値をわかりやすく表示するには以下のようにすると便利です。
$loadings を付けることで因子負荷の値のみを表示しています。
また、cutoff の値を 0.3 とすることで、因子負荷が 0.3 以下の値を非表示にできます。
result = fa( dat, nfactors = 5, fm = "minres", rotate = "oblimin", use = "complete.obs" )
print( result$loadings, digits = 2, cutoff = 0.3 )
##
## Loadings:
## MR2 MR1 MR3 MR5 MR4
## A1 -0.44
## A2 0.66
## A3 0.68
## A4 0.45
## A5 0.54
## C1 0.55
## C2 0.67
## C3 0.57
## C4 -0.64
## C5 -0.56
## E1 0.55
## E2 0.67
## E3 -0.41 0.30
## E4 -0.59
## E5 -0.42
## N1 0.83
## N2 0.78
## N3 0.70
## N4 0.47 0.40
## N5 0.48
## O1 0.52
## O2 -0.47
## O3 0.62
## O4 0.33 0.36
## O5 -0.54
##
## MR2 MR1 MR3 MR5 MR4
## SS loadings 2.5 1.96 1.98 1.89 1.56
## Proportion Var 0.1 0.08 0.08 0.08 0.06
## Cumulative Var 0.1 0.18 0.26 0.33 0.4011.8 因子軸の回転
上記の例では因子軸の回転方法としてオブリミン回転を指定していました。
因子を解釈するためには、因子が単純構造である方が便利です。単純構造とは、各項目の因子負荷が特定の 1 つの因子のみ大きな値を持ち、それ以外はゼロに近いような状態のことです。そのような状態にするために利用されるのが因子軸の回転です。
回転方法には様々な種類があり、それらは直行回転と斜行回転に大別されます。直行回転は因子間の相関がないことを想定した回転で、斜行回転は相関を想定します。因子間には相関があることが多いので、斜行回転の方がデータへの当てはまりは良くなりやすいです。
以下によく使われる回転方法をリストします
(カッコ内は fa() 関数の rotate 引数に指定する値)
直行回転
- バリマックス回転(“varimax”):因子負荷の平方の分散を最大化する方法
- クォーティマックス回転(“quartimax”):因子負荷量の分散の分散を最大化するように回転する
- ジオミン直行回転(“geominT”):因子負荷の各行のどこかに0に近い数が入るようにする
斜行回転
- プロマックス回転(“promax”):よく使われるが簡便法であるため必ずしも良い方法ではない
- 独立クラスター回転(“cluster”):各項目に1因子しか負荷しない状態を目指す
- オブリミン回転(“oblimin”):因子負荷の異なる列間の共分散の和を最小にする
- ジオミン斜行回転(“geominQ”):因子負荷の各行のどこかに0に近い数が入るようにする
どの回転方法を選ぶかですが、まず斜行回転(“geominQ” や、fa() 関数のデフォルトである “oblimin”)を使用して因子分析をすると良いでしょう。その結果で因子間相関係数がどれも小さかった場合(例えば 0.3 未満など)、因子間に相関はないとみなして、直行回転(“geominT” や “varimax”)を用いて再び因子分析を行います。
回転方法についての解説は先述のスライドも参考にして下さい。
https://www.slideshare.net/simizu706/r-42283141
11.9 因子の解釈
適切な回転方法を選び、それを用いた因子分析によって因子負荷の推定が終わったら、次に因子の解釈を行います。つまり、それぞれの因子と関連の強い(因子負荷の大きい)項目を確認して、その因子が何を測定しているものであるのか判断します。
今回の結果の場合、第1因子は E1〜E5、第2因子は N、第3因子は C1〜C5、第4因子は O1〜O5、第5因子は A1〜A5 と強い関連を持つという結果になっています。
項目の分類について再掲します。
— Agreeableness(協調性・調和性):A1からA5
— Conscientiousness(勤勉性・誠実性):C1からC5
— Extraversion(外向性):E1からE5
— Neuroticism(神経症傾向・情緒不安定性):N1からN5
— Openness(開放性・経験への開放性):O1からO5
したがって、第1因子は外向性、第2因子は神経症傾向、第3因子は勤勉性、第4因子は開放性、第5因子は協調性に対応する因子であることが確認できました。
11.10 練習問題
別のデータを使って因子分析を行なってみましょう。
11.10.1 データ
車を購入する際に重視する要素ついての質問紙に対する 90 人分の回答データです。質問項目は全部で 14 個あり、それぞれについて 1 から 5 までの 5 段階で回答しました(より重視する場合に大きな数字で回答する)。
具体的な質問項目は以下のものでした。
— Price
— Safety
— Exterior looks
— Space and comfort
— Technology
— After sales service
— Resale value
— Fuel type
— Fuel efficiency
— Color
— Maintenance
— Test drive
— Product reviews
11.10.2 データの読み込み
csv ファイルを https://htsuda.net/dataset/car.csv にアップロードしています。
以下のようにして R に直接読み込めます。
dat = read.csv( "https://htsuda.net/dataset/car.csv", header = T )
head( dat, 1 ) # データの確認
## Price Safety Exterior_Looks Space_comfort Technology After_Sales_Service
## 1 4 4 5 4 3 4
## Resale_Value Fuel_Type Fuel_Efficiency Color Maintenance Test_drive
## 1 5 4 4 2 4 2
## Product_reviews Testimonials
## 1 4 311.10.4 解答例
KMO
KMO( dat )
## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = dat)
## Overall MSA = 0.61
## MSA for each item =
## Price Safety Exterior_Looks Space_comfort
## 0.72 0.47 0.55 0.61
## Technology After_Sales_Service Resale_Value Fuel_Type
## 0.65 0.62 0.63 0.68
## Fuel_Efficiency Color Maintenance Test_drive
## 0.62 0.56 0.61 0.64
## Product_reviews Testimonials
## 0.69 0.50全体指標が 0.6 以上なのでOK。
因子数を決める
# スクリープロットを描く
fa.parallel( dat, fa = "fa", use = "complete.obs" ) # スクリープロットを表示
abline( h = 0 ) # y = 0 の横線を追加
# Parallel analysis suggests that the number of factors = 4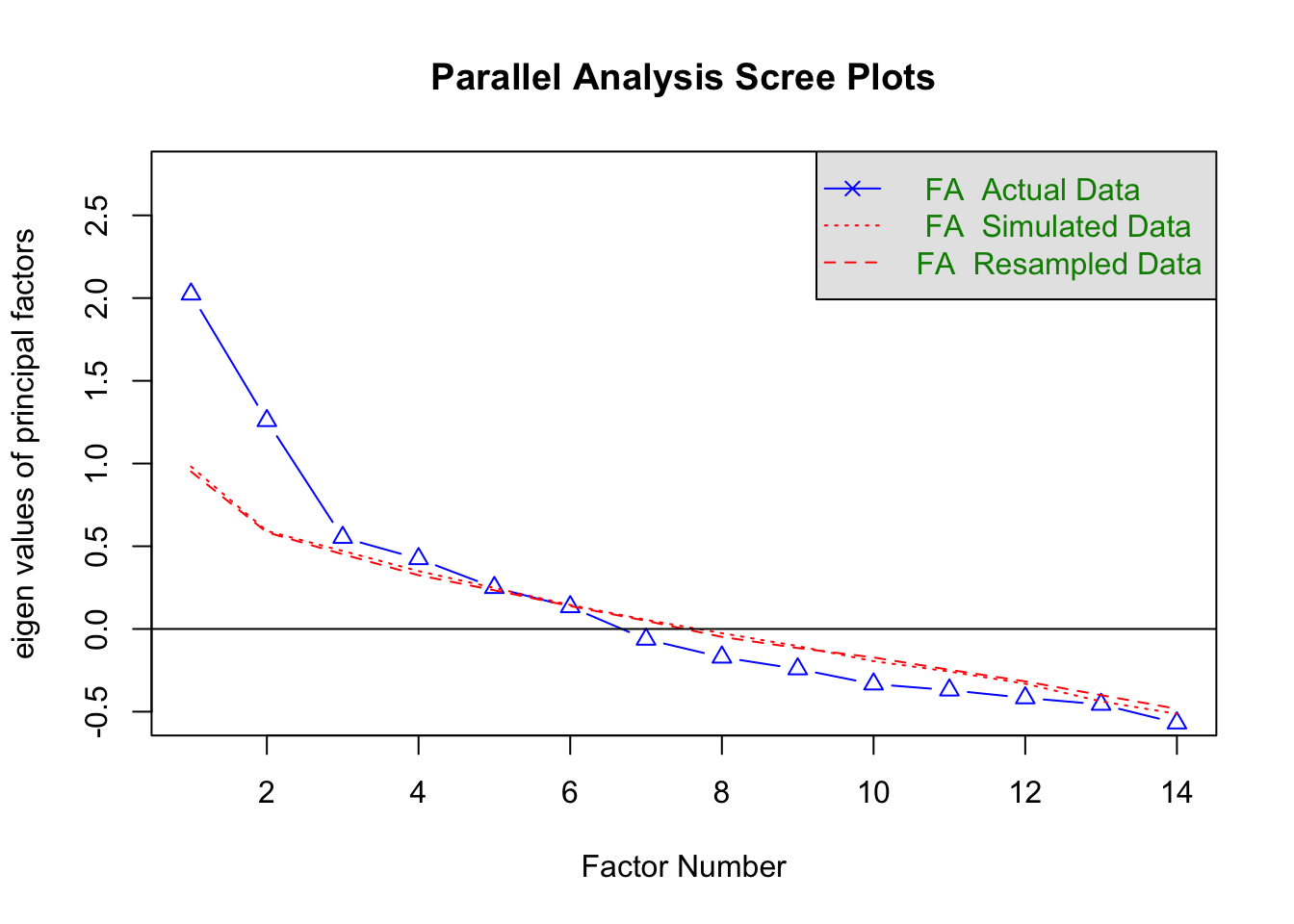
# MAP/BIC 基準の因子数の計算
VSS( dat, n = 8 )
# 略
# The Velicer MAP achieves a minimum of 0.03 with 2 factors
# BIC achieves a minimum of -192.72 with 2 factors
# 略平行分析は 4、MAP/BIC 基準は 2 と、意見が分かれています。
2〜4 の因子数のそれぞれの場合ごとの因子構造を確認してみます。
result = fa( dat, nfactors = 4, fm = "minres", rotate = "oblimin", use = "complete.obs" )
fa.diagram( result )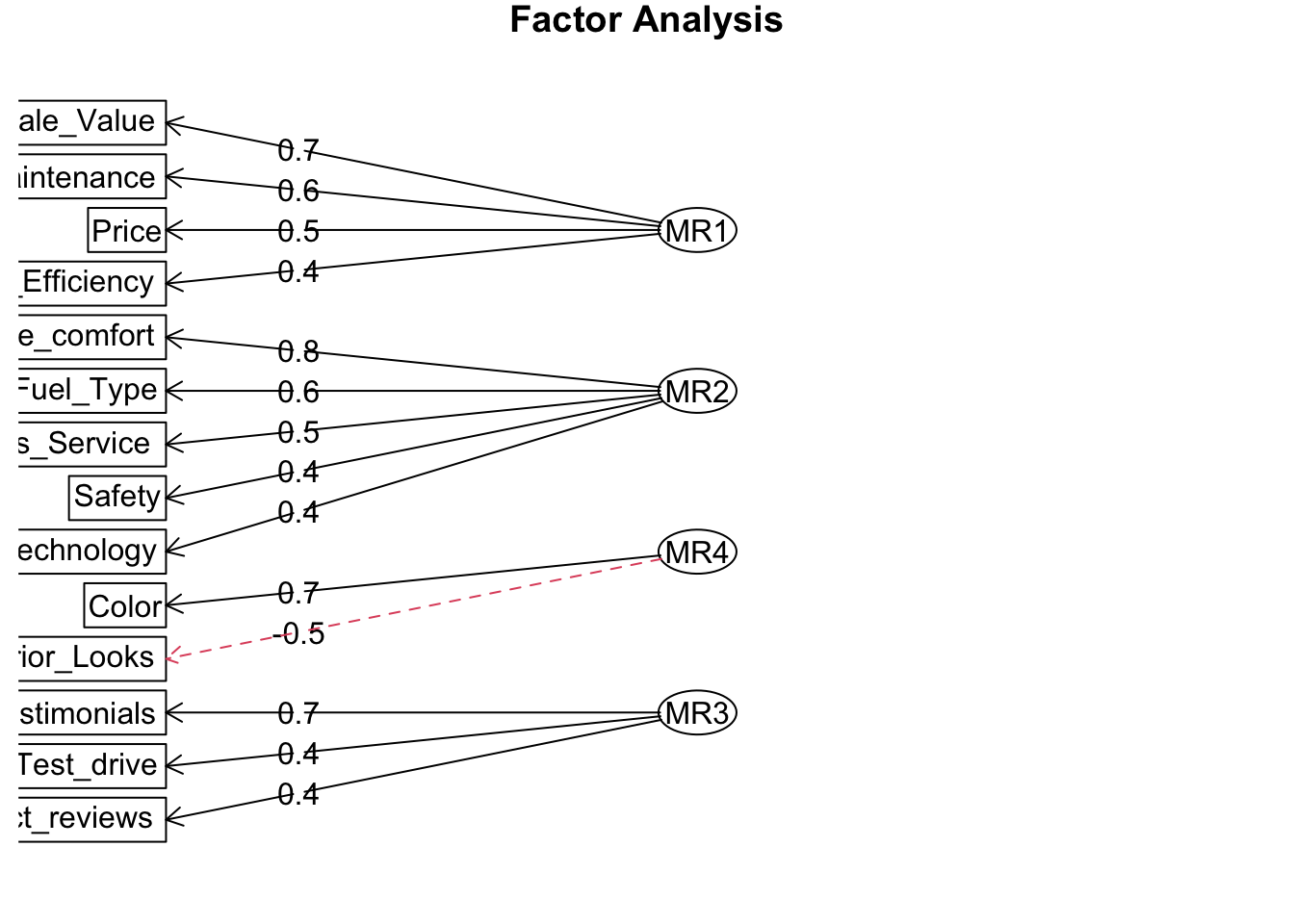
result = fa( dat, nfactors = 3, fm = "minres", rotate = "oblimin", use = "complete.obs" )
fa.diagram( result )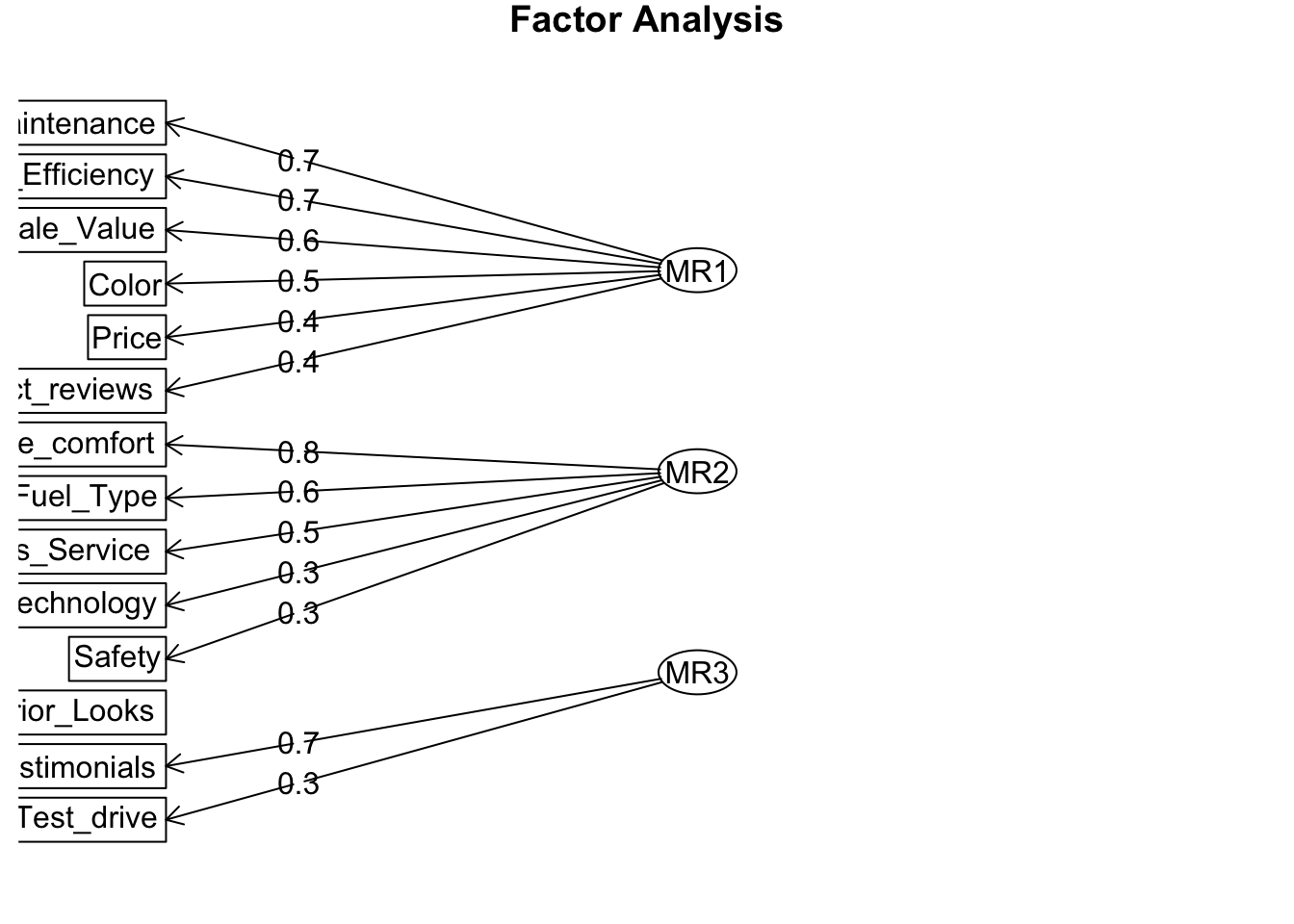
result = fa( dat, nfactors = 2, fm = "minres", rotate = "oblimin", use = "complete.obs" )
fa.diagram( result )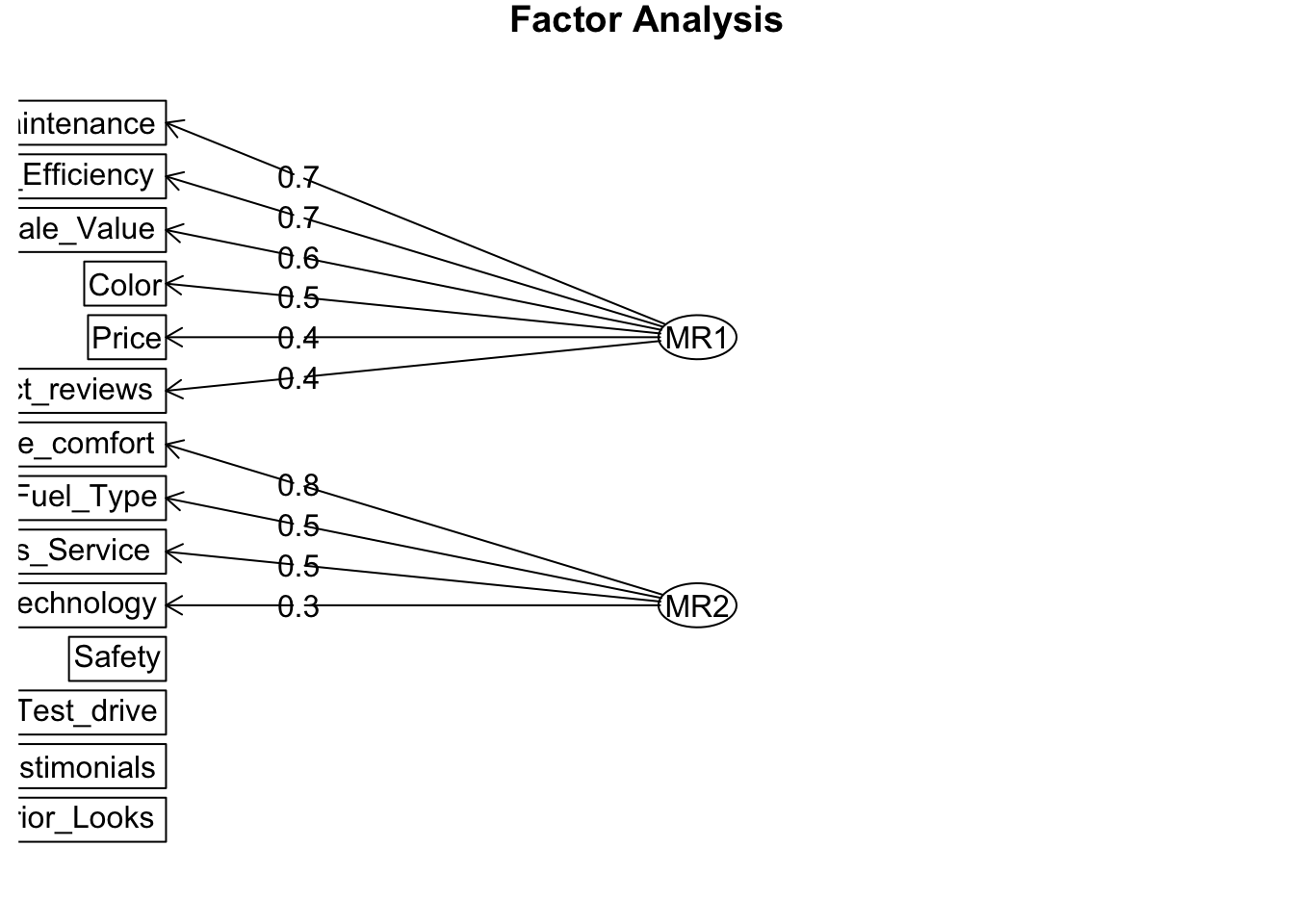
因子数が 2 や 3 の場合には使われずに残る変数が見られるので、因子数は 4 にすることにします。
因子構造の確認
result = fa( dat, nfactors = 4, fm = "minres", rotate = "oblimin", use = "complete.obs" )
print( result$loadings, digits = 2, cutoff = 0.3 )
##
## Loadings:
## MR1 MR2 MR4 MR3
## Price 0.54
## Safety -0.33 0.36
## Exterior_Looks -0.55
## Space_comfort 0.78
## Technology 0.36
## After_Sales_Service 0.54
## Resale_Value 0.73
## Fuel_Type 0.57
## Fuel_Efficiency 0.43 0.31
## Color 0.73
## Maintenance 0.56
## Test_drive 0.36
## Product_reviews 0.34 0.36
## Testimonials 0.68
##
## MR1 MR2 MR4 MR3
## SS loadings 1.64 1.64 1.05 0.97
## Proportion Var 0.12 0.12 0.08 0.07
## Cumulative Var 0.12 0.23 0.31 0.38この結果から、
因子1: 価格・転売額・燃費・保守性
因子2: 安全・快適性・技術・サービス・燃料タイプ
因子3: テスト走行・商品レビュー・推薦文
因子4: 外見・色
という関連がわかりました。