8 回帰分析

8.1 概要

回帰分析という統計手法は、独立変数（説明変数・予測変数）と従属変数（被説明変数・目的変数・応答変数）の関係を記述するのに使われます。

回帰分析を使うことで、

目的変数と関連のある説明変数を特定したり、
変数間の関係式を記述したり、
説明変数から目的変数を予測したり

することができます。

8.2 データセット

datarium パッケージの marketing データを利用します。

library( datarium )
mkt = as.data.frame( marketing )
head( mkt, 3 )
##   youtube facebook newspaper sales
## 1  276.12    45.36     83.04 26.52
## 2   53.40    47.16     54.12 12.48
## 3   20.64    55.08     83.16 11.16

図のパラメータを調整しておきます。

par(
    las = 1,
    cex.lab = 1.5,
    cex.axis =1.3
)

8.3 線形単回帰

lm( formula = 回帰式, data = データフレーム ) という関数を使います。
回帰係数などの計算結果は summary() 関数で確認できます。

回帰式は 目的変数 ~ 説明変数 という形式で書きます。

fit = lm( formula = sales ~ youtube, data = mkt )
summary( fit )
## 
## Call:
## lm(formula = sales ~ youtube, data = mkt)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.0632  -2.3454  -0.2295   2.4805   8.6548 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 8.439112   0.549412   15.36   <2e-16 ***
## youtube     0.047537   0.002691   17.67   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.91 on 198 degrees of freedom
## Multiple R-squared:  0.6119, Adjusted R-squared:  0.6099 
## F-statistic: 312.1 on 1 and 198 DF,  p-value: < 2.2e-16

par( mar = c( 4.5, 4.5, 1, 1 ) )
plot( x = mkt$youtube, mkt$sales,
    xlab = "Youtube [unit: 1000 dollars]", ylab = "Sales" )
abline( fit, col = "#2792b3", lwd = 4 )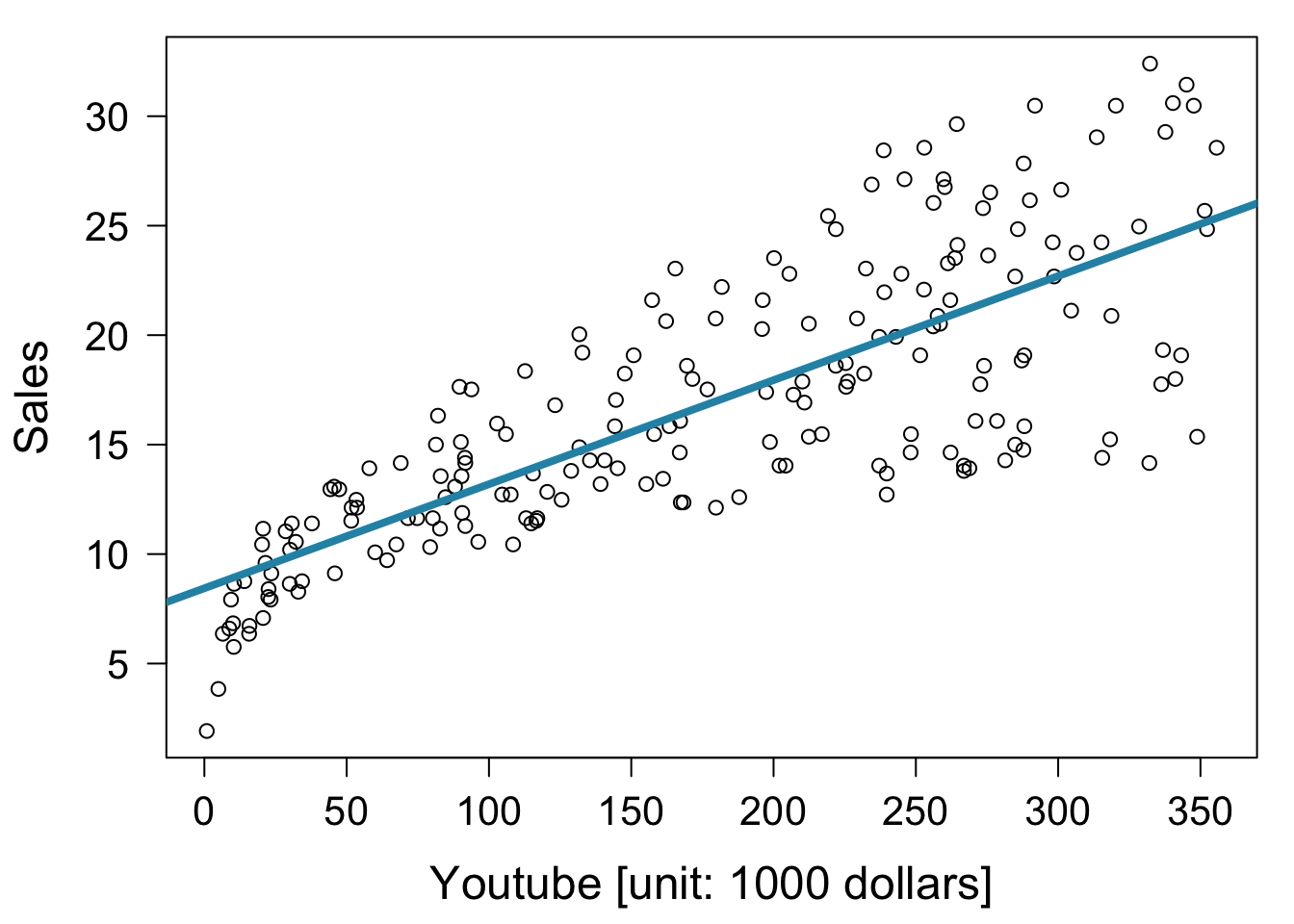

8.4 多項式回帰

2次式による回帰。
formula において2次の項を I() で囲う必要があります。

fit2 = lm( formula = sales ~ youtube + I( youtube^2 ), data = mkt )
summary( fit2 )
## 
## Call:
## lm(formula = sales ~ youtube + I(youtube^2), data = mkt)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9.2213 -2.1412 -0.1874  2.4106  9.0117 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   7.337e+00  7.911e-01   9.275  < 2e-16 ***
## youtube       6.727e-02  1.059e-02   6.349 1.46e-09 ***
## I(youtube^2) -5.706e-05  2.965e-05  -1.924   0.0557 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.884 on 197 degrees of freedom
## Multiple R-squared:  0.619,  Adjusted R-squared:  0.6152 
## F-statistic: 160.1 on 2 and 197 DF,  p-value: < 2.2e-16

plot( x = mkt$youtube, mkt$sales,
    xlab = "Youtube [unit: 1000 dollars]", ylab = "Sales" )
lines( sort( mkt$youtube ), fitted( fit2 )[ order( mkt$youtube ) ],
    , col = "#2792b3", lwd = 3 )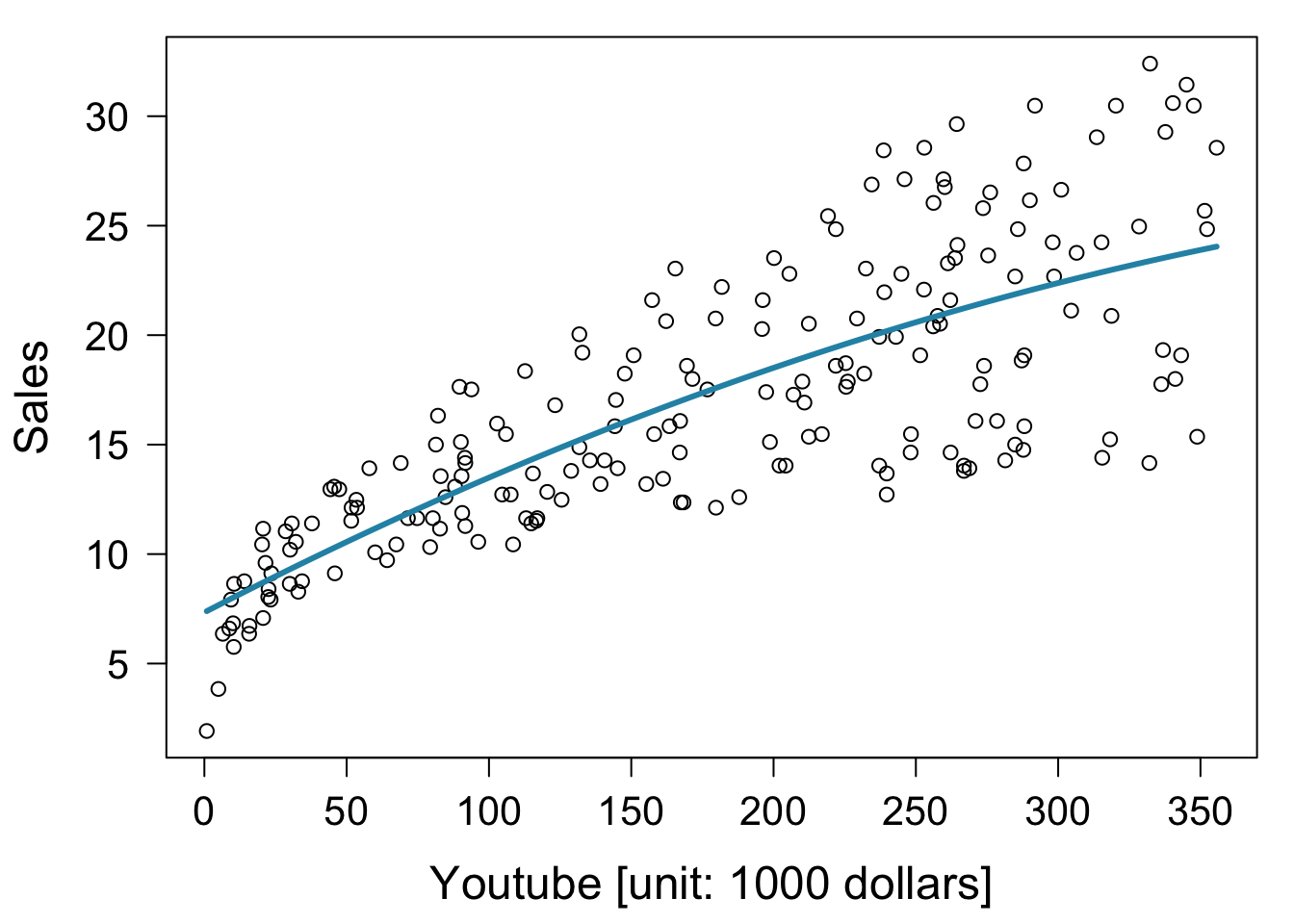

3次式による回帰。

fit3 = lm( sales ~ youtube + I( youtube^2 ) + I( youtube^3 ), data = mkt )
summary( fit3 )
## 
## Call:
## lm(formula = sales ~ youtube + I(youtube^2) + I(youtube^3), data = mkt)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9.5680 -2.2679 -0.1077  2.4227  8.8518 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   6.504e+00  1.037e+00   6.272 2.23e-09 ***
## youtube       9.643e-02  2.580e-02   3.738 0.000243 ***
## I(youtube^2) -2.627e-04  1.685e-04  -1.559 0.120559    
## I(youtube^3)  3.869e-07  3.121e-07   1.240 0.216519    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.879 on 196 degrees of freedom
## Multiple R-squared:  0.622,  Adjusted R-squared:  0.6162 
## F-statistic: 107.5 on 3 and 196 DF,  p-value: < 2.2e-16

plot( x = mkt$youtube, mkt$sales,
    xlab = "Youtube [unit: 1000 dollars]", ylab = "Sales" )
lines( sort( mkt$youtube ), fitted( fit3 )[ order( mkt$youtube ) ],
    , col = "#2792b3", lwd = 3 )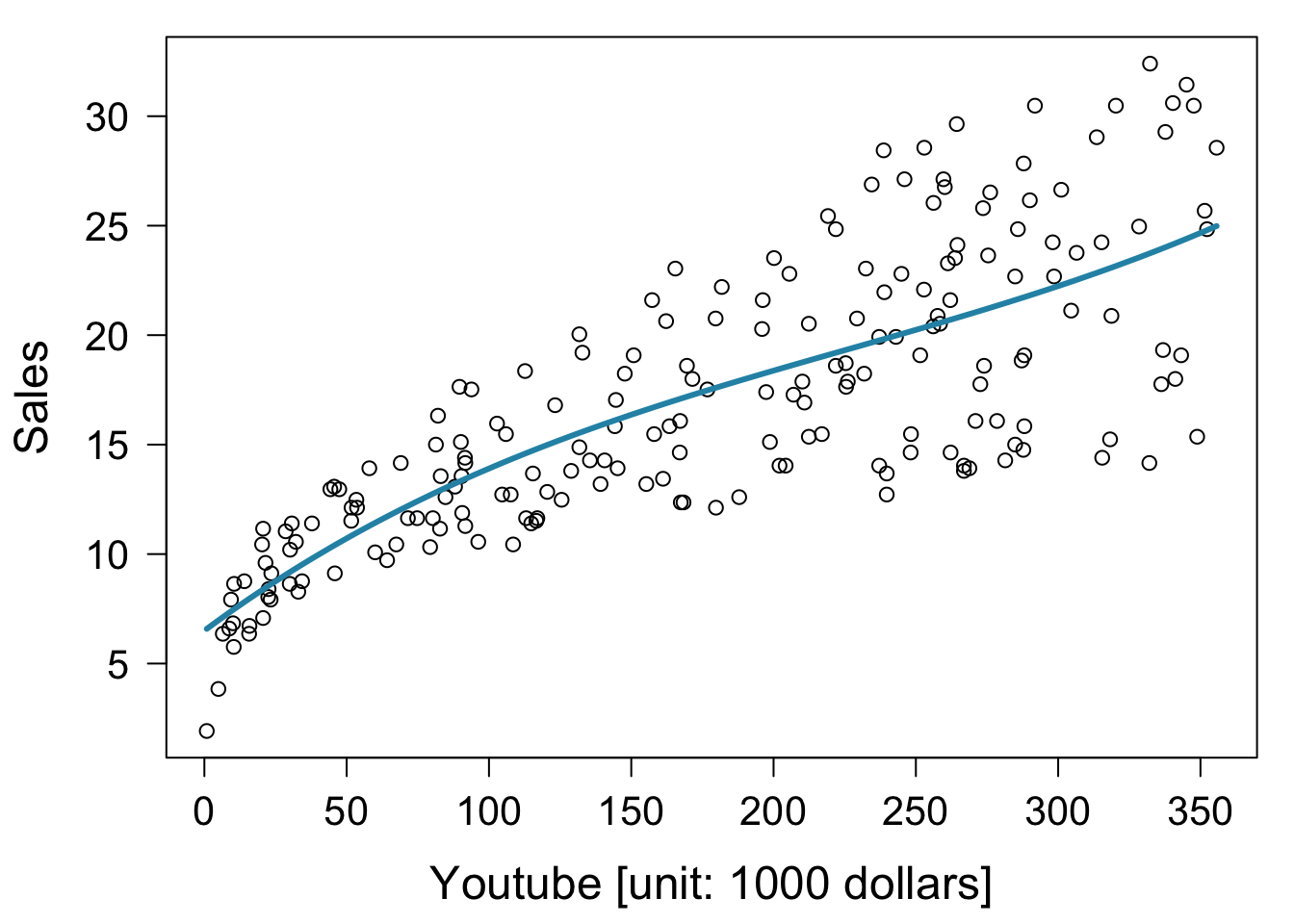

8.5 car パッケージを利用した回帰直線の作図

car パッケージの scatterplot() 関数を利用した作図。

library( car )

scatterplot( sales ~ youtube, data = mkt, spread = F, boxplots = F,
    smooth = F, regLine = list( col = "#2792b3", lwd = 3 ), col = "black",
    xlab = "Youtube [unit: 1000 dollars]", ylab = "Sales",
    las = 1, cex.lab = 1.5, cex.axis =1.3 )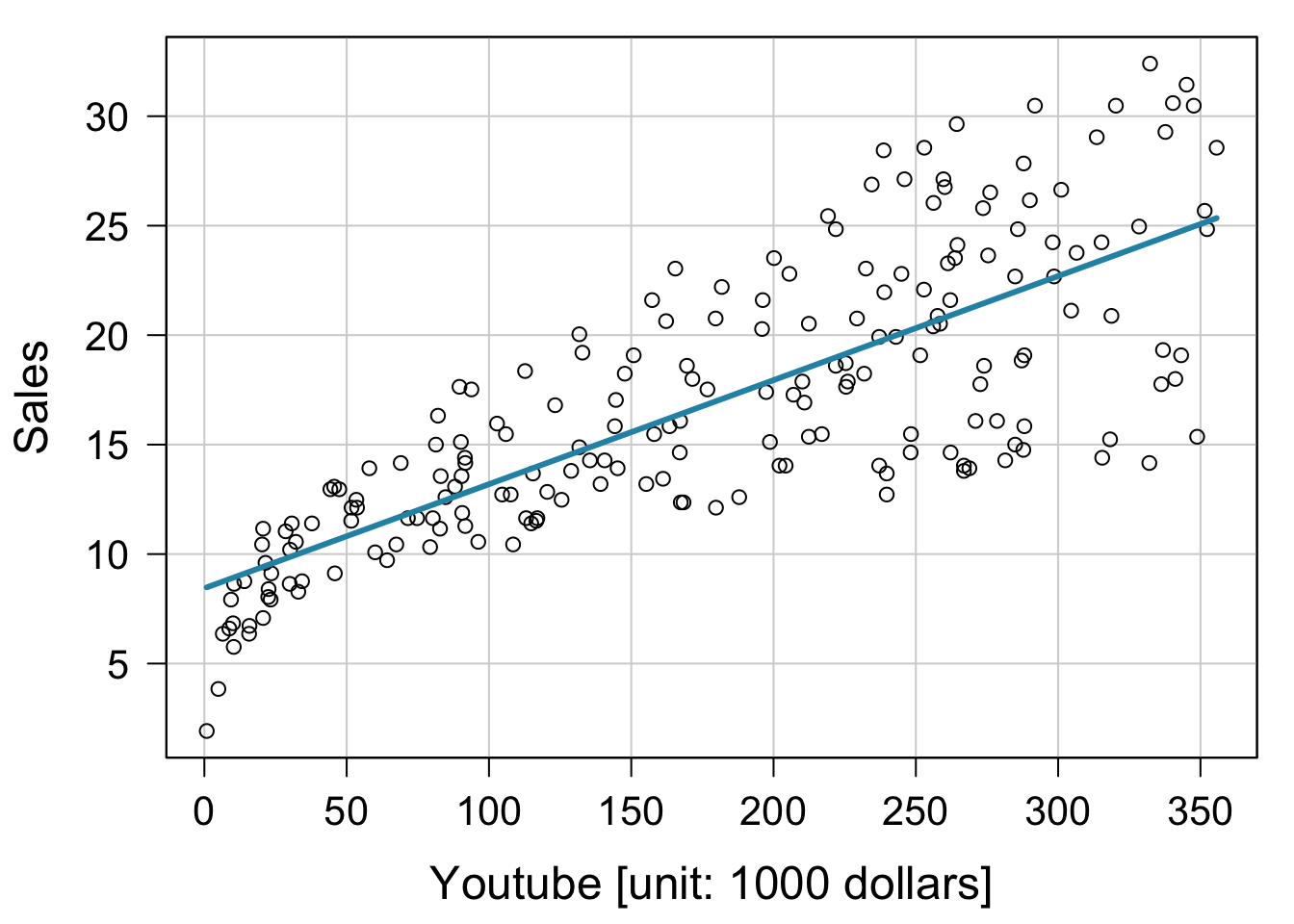

car パッケージの scatterplotMatrix() 関数を利用した作図。

library( car )

scatterplotMatrix( mkt, spread = F, smooth = F,
    regLine = list( col = "#2792b3", lwd = 3 ), col = "black", cex = .5 )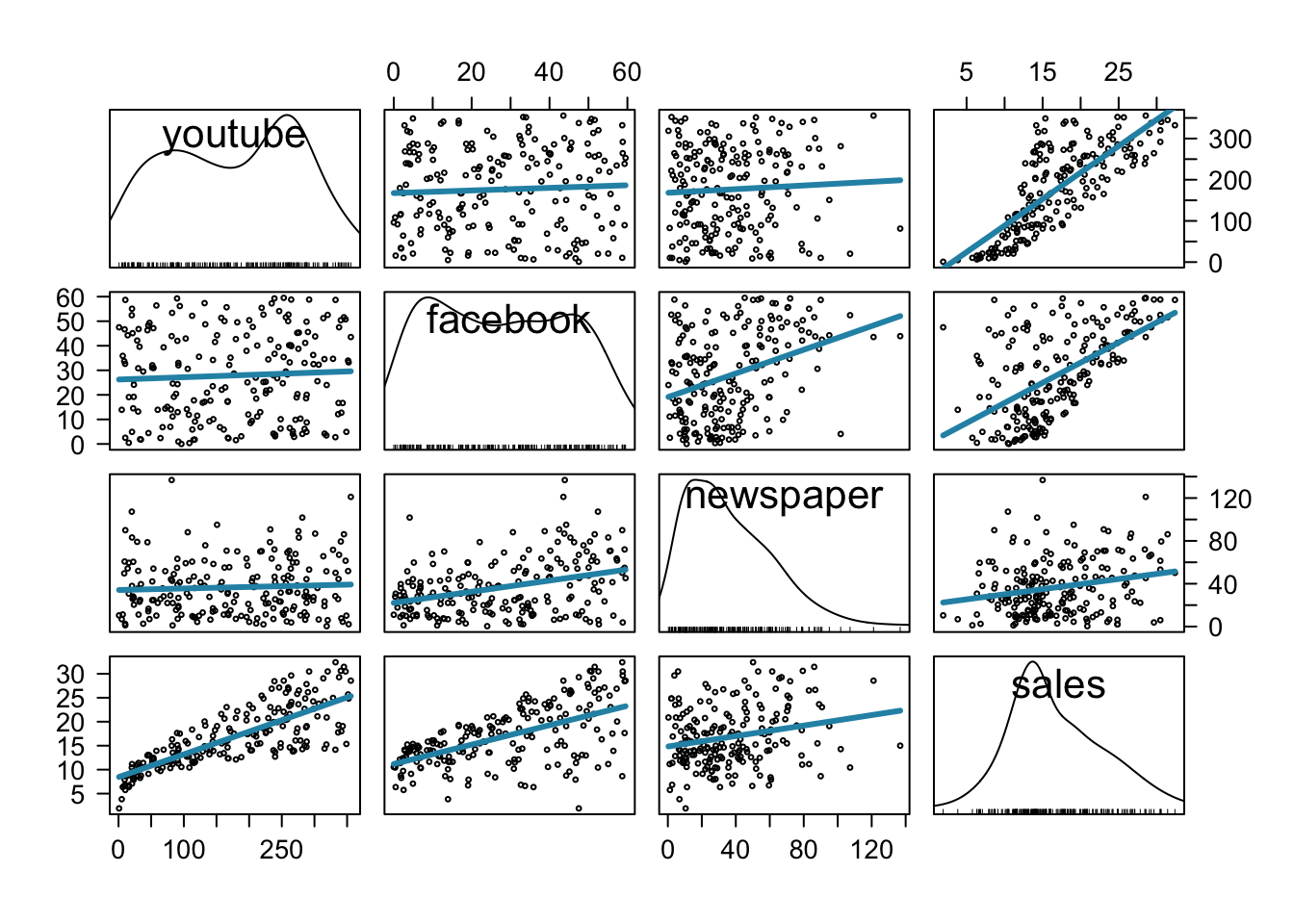

相関係数の計算。

cor( mkt )
##              youtube   facebook  newspaper     sales
## youtube   1.00000000 0.05480866 0.05664787 0.7822244
## facebook  0.05480866 1.00000000 0.35410375 0.5762226
## newspaper 0.05664787 0.35410375 1.00000000 0.2282990
## sales     0.78222442 0.57622257 0.22829903 1.0000000

8.6 重回帰

重回帰モデル。

fit = lm( sales ~ youtube + facebook + newspaper, data = mkt )
summary( fit )
## 
## Call:
## lm(formula = sales ~ youtube + facebook + newspaper, data = mkt)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.5932  -1.0690   0.2902   1.4272   3.3951 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.526667   0.374290   9.422   <2e-16 ***
## youtube      0.045765   0.001395  32.809   <2e-16 ***
## facebook     0.188530   0.008611  21.893   <2e-16 ***
## newspaper   -0.001037   0.005871  -0.177     0.86    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.023 on 196 degrees of freedom
## Multiple R-squared:  0.8972, Adjusted R-squared:  0.8956 
## F-statistic: 570.3 on 3 and 196 DF,  p-value: < 2.2e-16

説明変数の交互作用を含めるときは、コロン記号を使います。
以下の例では youtube と facebook の交互作用項を加えています。

fit = lm( sales ~ youtube + facebook + youtube:facebook, data = mkt )
summary( fit )
## 
## Call:
## lm(formula = sales ~ youtube + facebook + youtube:facebook, data = mkt)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -7.6039 -0.4833  0.2197  0.7137  1.8295 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      8.100e+00  2.974e-01  27.233   <2e-16 ***
## youtube          1.910e-02  1.504e-03  12.699   <2e-16 ***
## facebook         2.886e-02  8.905e-03   3.241   0.0014 ** 
## youtube:facebook 9.054e-04  4.368e-05  20.727   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.132 on 196 degrees of freedom
## Multiple R-squared:  0.9678, Adjusted R-squared:  0.9673 
## F-statistic:  1963 on 3 and 196 DF,  p-value: < 2.2e-16

交互作用の様子を視覚化するには effect() 関数が便利です。

library( effects )

plot( effect( "youtube:facebook", fit, ,
    list( facebook = c( 0, 30, 60 ) ) ), multiline = T)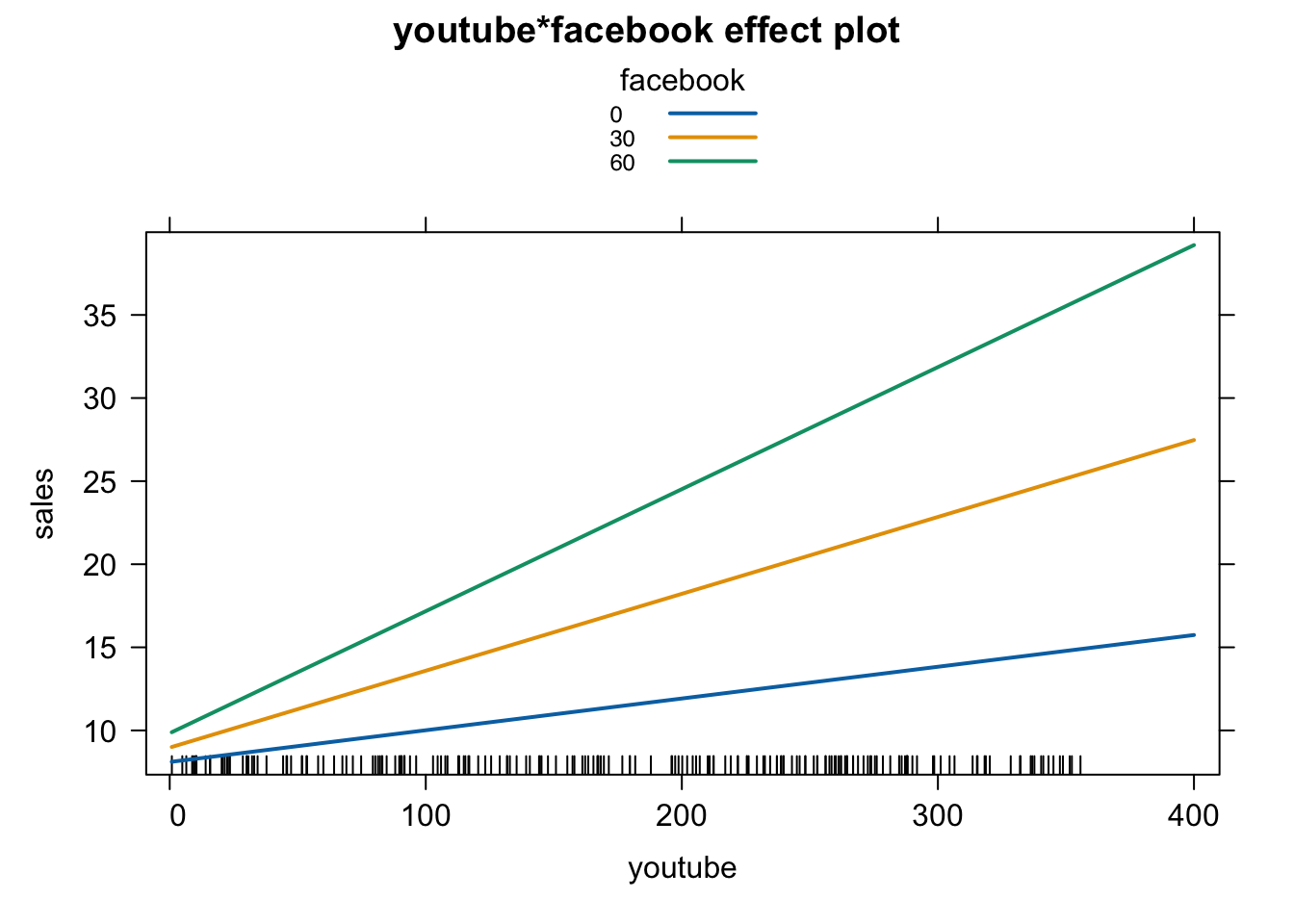

facebook の値が大きいほど、youtube と sales の関係が強くなる（スロープが急峻になる）ことがわかります。

8.7 回帰の診断方法

回帰分析はいくつかの前提条件を想定しています。

正規性（Normality）
独立性（Independence）
線形性（Linearity）
等分散性（Homoscedasticity）

回帰分析をする際はこれらの条件が満たされているかをチェックしておく必要があります。

8.7.1 正規性（Normality）

目的変数が正規分布に従うという条件です。
もしそうなっていれば、Q-Q プロットにおいてデータは対角線上に分布します。

library( car )

fit = lm( sales ~ youtube + facebook + newspaper, data = mkt )
qqPlot( fit, labels = row.names( mkt ), id.method = "identity", simulate = T )
## [1]   6 131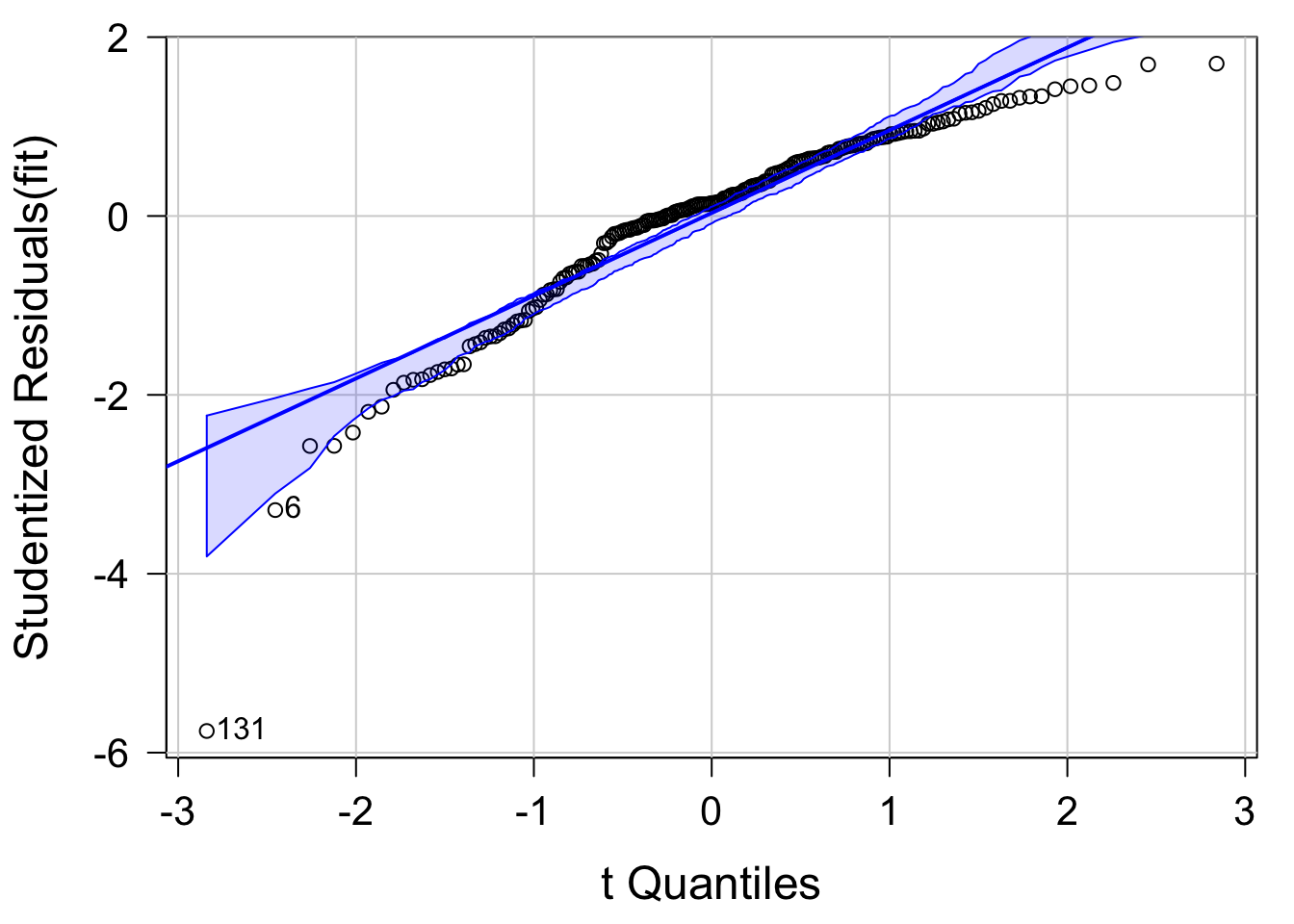

データは直線になっておらず、値が小さい場合や大きい場合に実測値はモデルの予測よりも小さくなっています。

左下の 131 のデータが特に大きな外れ値になっています。
外れ値であることは残差やスチューデント化残差の大きさに反映されます。

fitted( fit )[ 131 ] # モデルの予測値
##      131 
## 12.51322

residuals( fit )[ 131 ] # 残差（= 実測値 - 予測値）
##       131 
## -10.59322

rstudent( fit )[ 131 ] # スチューデント化残差（= 残差 / 標準偏差）
##       131 
## -5.757983

Q-Q プロットから 131 と 6 のデータが外れ値であるようなので、それらを除外して再度 Q-Q プロットを作図してみます。

library( car )

newfit = lm( sales ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
qqPlot( newfit, labels = row.names( mkt ), id.method = "identity", simulate = T )
##  36 127 
##  35 126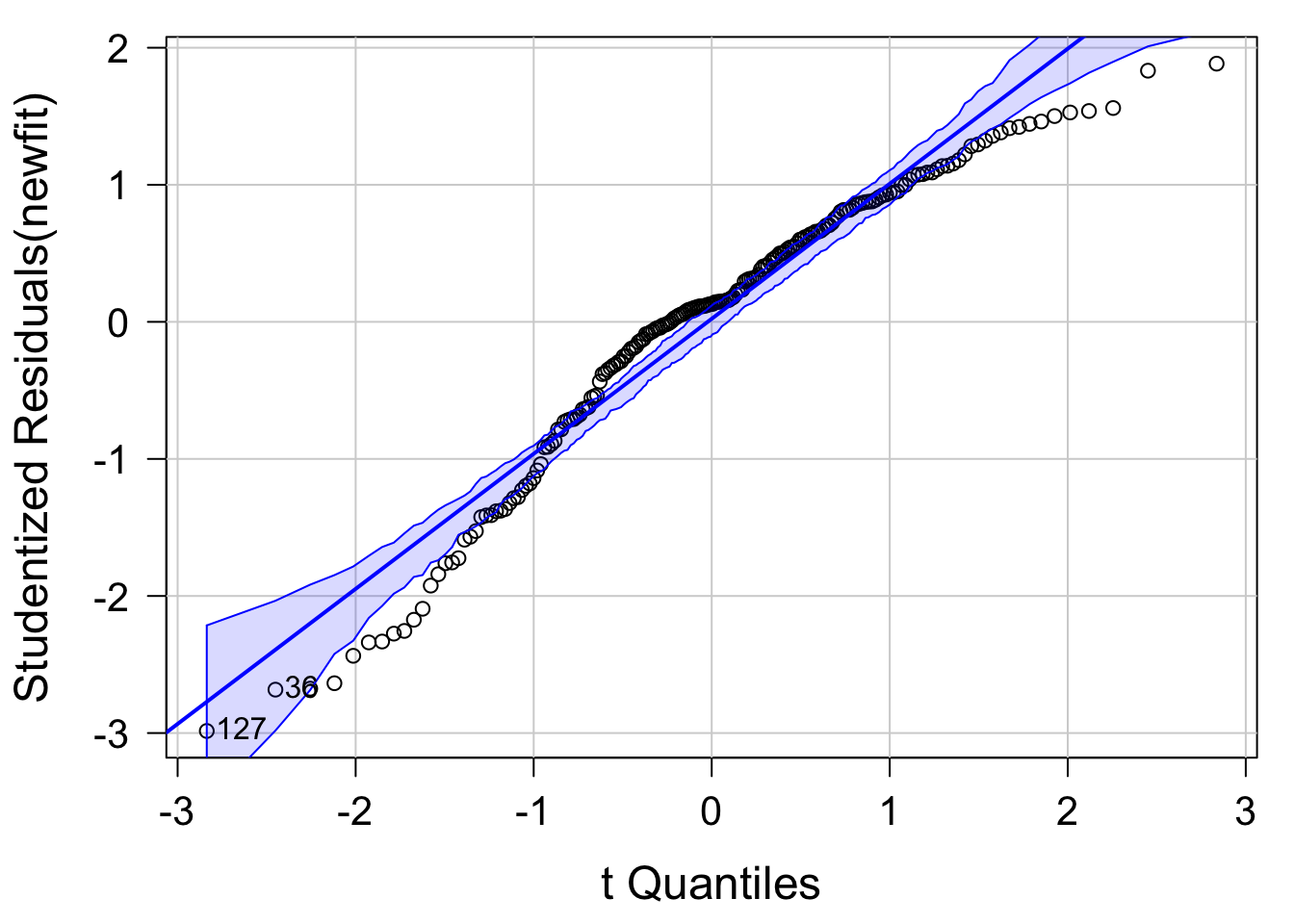

正規性を満たすかを確認するには誤差分布の形状を確認するのもわかりやすい方法です。
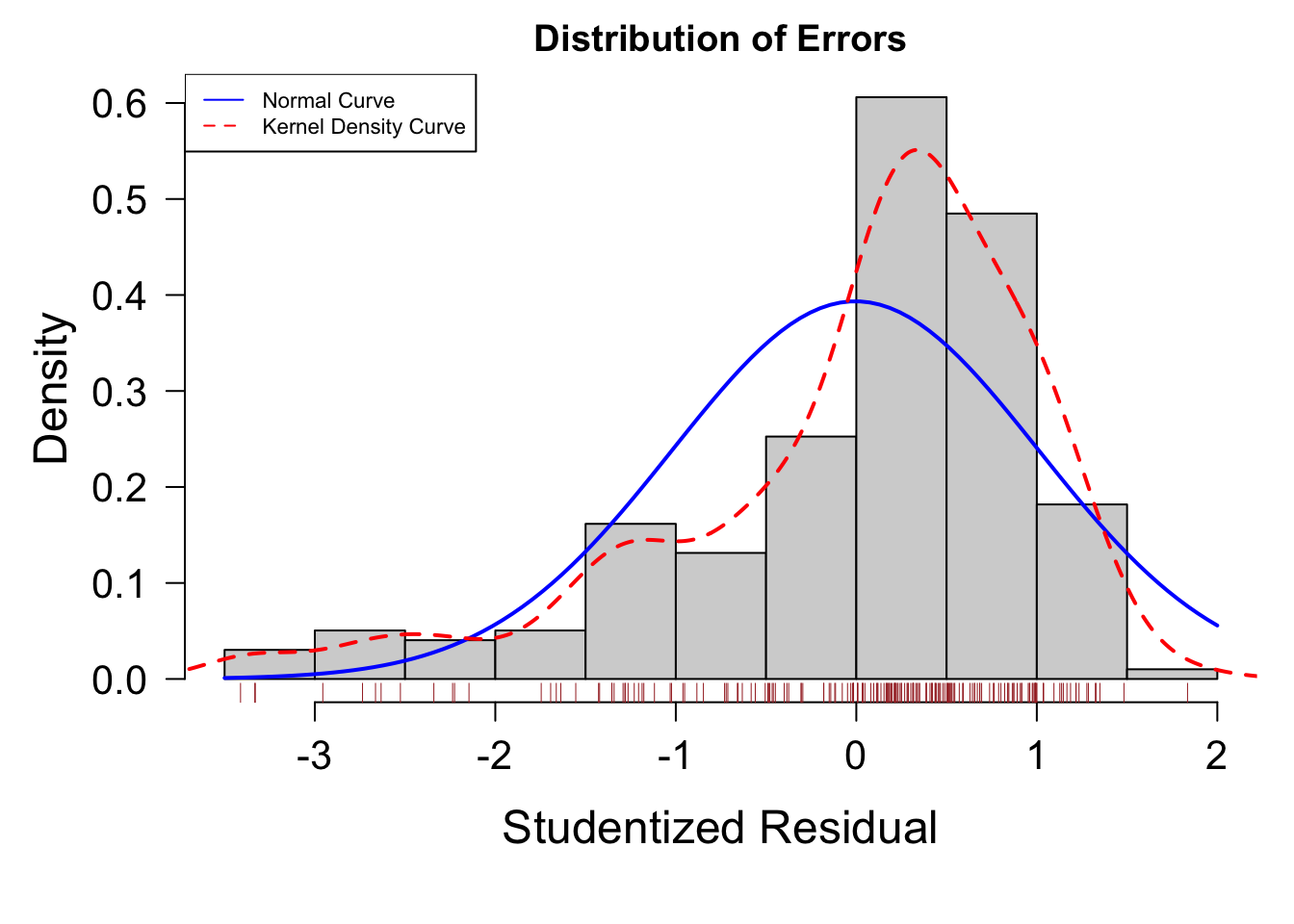
以下の図では誤差のヒストグラムを表示します。

residplot = function( fit, nbreaks = 10 ){
    z = rstudent( fit )
    hist( z, breaks = nbreaks, freq = F,
        xlab = "Studentized Residual", main = "Distribution of Errors" )
    rug( jitter( z ), col = "brown" )
    curve( dnorm( x, mean = mean( z ), sd = sd( z ) ), add = T, col = "blue", lwd = 2 )
    lines( density( z )$x, density( z )$y, col = "red", lwd = 2, lty = 2 )
    legend( "topleft", legend = c( "Normal Curve", "Kernel Density Curve"),
        lty = 1:2, col = c( "blue", "red" ), cex =.7 )
}

residplot( fit )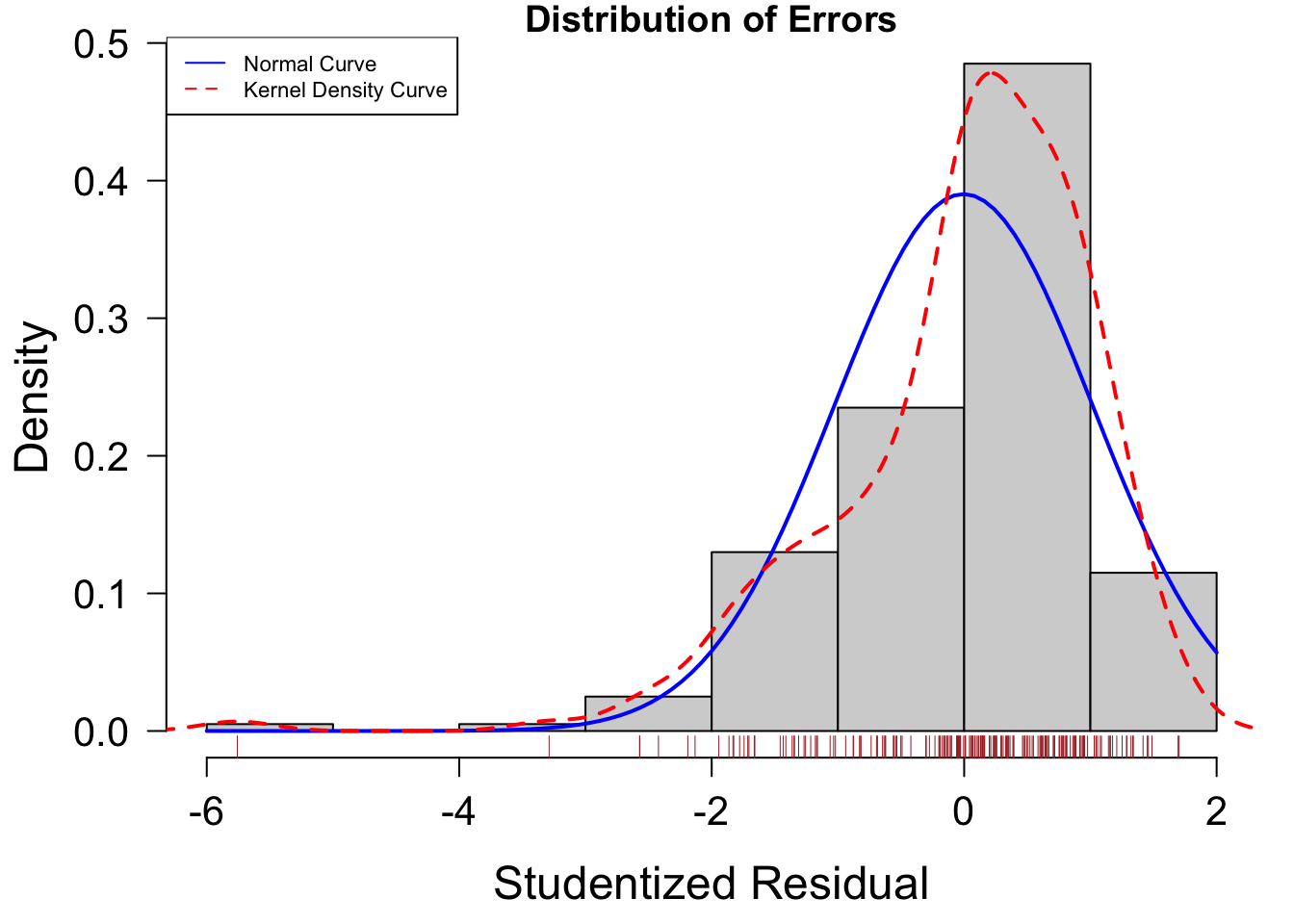

この図でも分布があまり左右対称ではなく、また左端に外れ値があることなどが見て取れます。

8.7.2 独立性（Independence）

各観測が独立でなければならないという条件です。
時系列データや階層性のあるデータの場合にはこの条件が満たされません。

car パッケージの durbinWatsonTest() 関数は Durbin-Watson 検定によって系列的な相関について調べることができます。

car::durbinWatsonTest( fit )
##  lag Autocorrelation D-W Statistic p-value
##    1     -0.04687792      2.083648    0.59
##  Alternative hypothesis: rho != 0

p > 0.05 であるため自己相関があるとは言えません（つまり独立性が示唆される）。

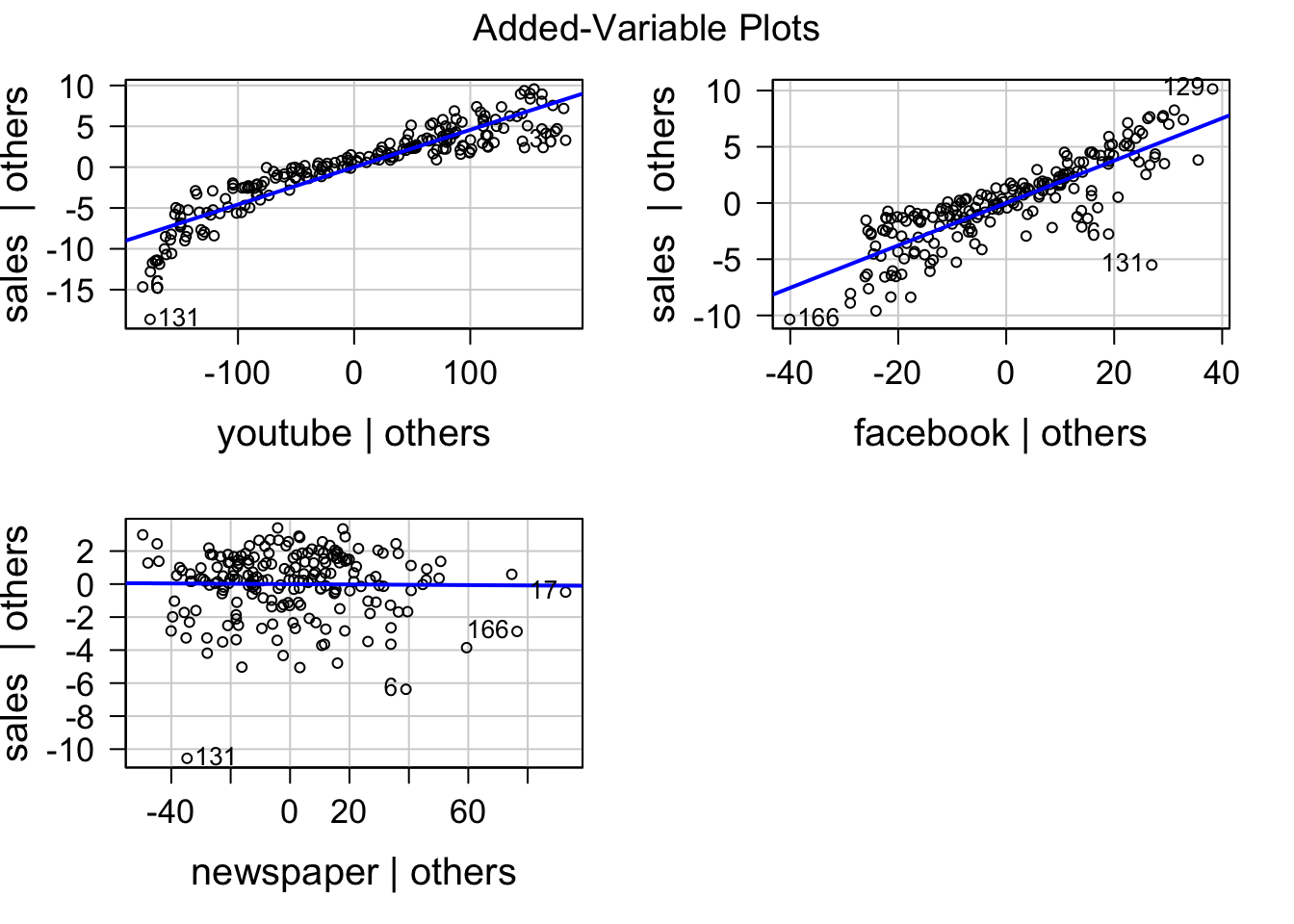
8.7.3 線形性（Linearity）

目的変数が説明変数と線形な関係を持つという条件です。

Component plus residual プロットを使うと線形性を確認できます。

par( mar = c( 4.5, 4.5, 3, 1 ) )
car::crPlots( fit )

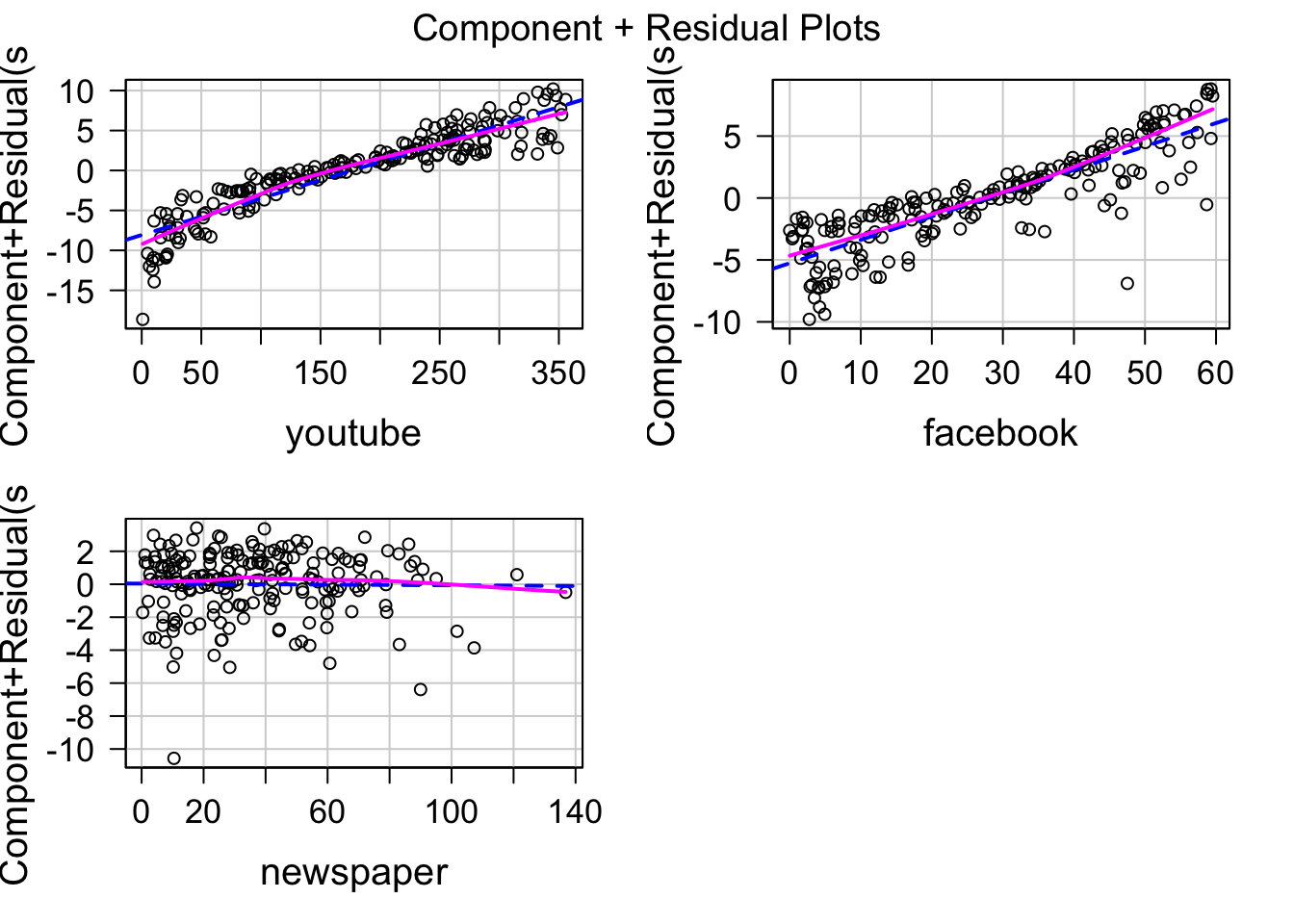
直線は線形モデルのフィットで、曲線は Loes による曲線です。
どの図（説明変数）でも2つの線が重なっているので、線形性は満たされていると考えられます。

8.7.4 等分散性（Homoscedasticity）

目的変数の分散が位置によらず一定であるという条件です。
もし等分散性が満たされていれば残差の値は予測値の値に依存しない（つまり水平な分布）になるはずです。

car::ncvTest( fit )
## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 5.355982, Df = 1, p = 0.020651

par( mar = c( 4.5, 4.5, 2, 1 ) )
spreadLevelPlot( fit )
## 
## Suggested power transformation:  1.499852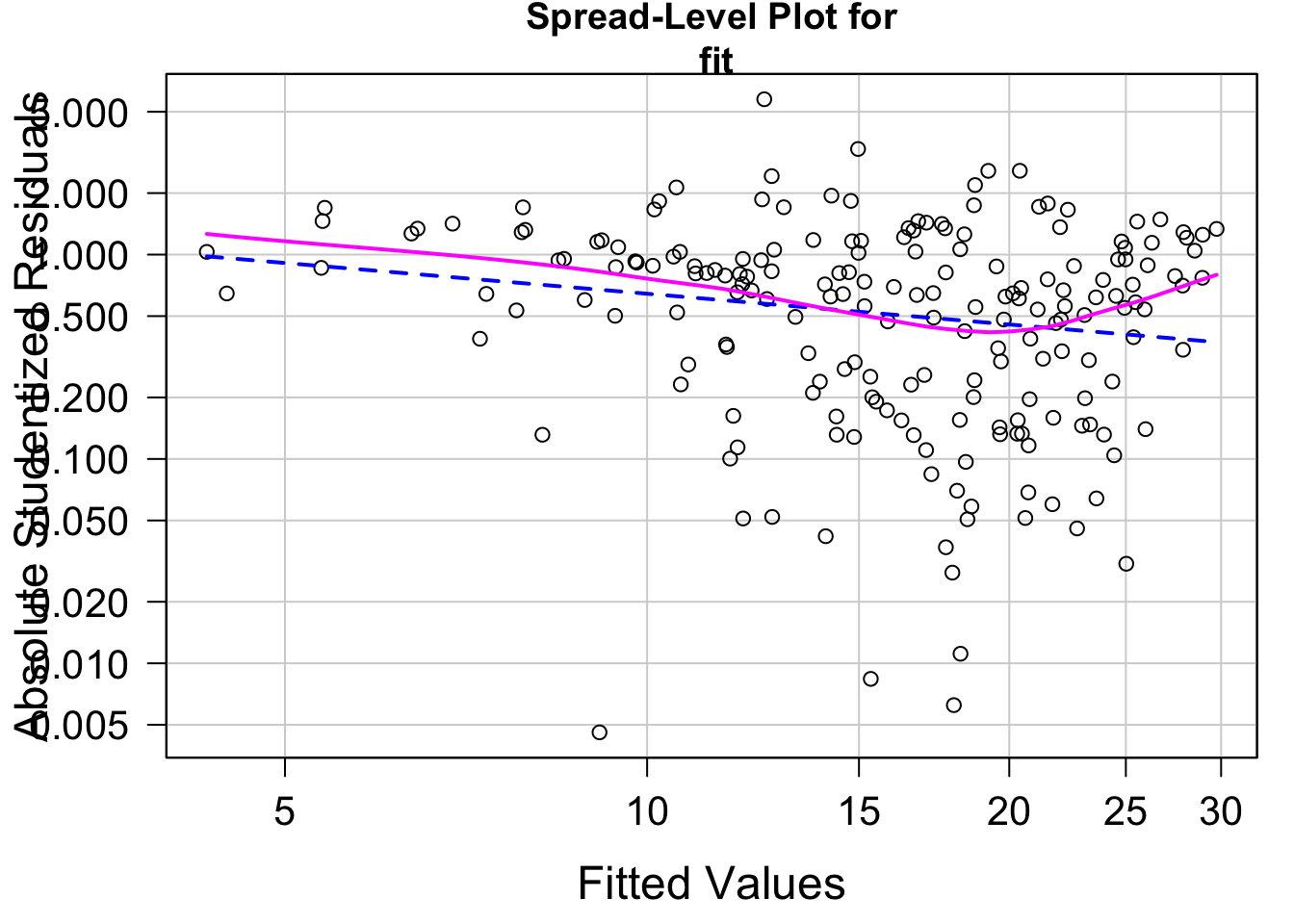

p 値が 0.05 未満であり、等分散ではないという結果になっています。
（この検定は等分散であることを帰無仮説とし、予測値の値によって分散が異なることを対立仮説とします。p < .05 で帰無仮説が棄却されると、等分散ではないという仮説が支持されます）

図を見ると右下がりの分布になっており、予測値の値が小さいほど残差が大きく、確かに等分散ではないと見て取れます。

8.7.5 診断

gvlma() 関数を使うと線形モデルの仮定の妥当性についての様々な基準についての検定を行えます。

library( gvlma )

summary( gvlma( fit ) )
## 
## Call:
## lm(formula = sales ~ youtube + facebook + newspaper, data = mkt)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.5932  -1.0690   0.2902   1.4272   3.3951 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.526667   0.374290   9.422   <2e-16 ***
## youtube      0.045765   0.001395  32.809   <2e-16 ***
## facebook     0.188530   0.008611  21.893   <2e-16 ***
## newspaper   -0.001037   0.005871  -0.177     0.86    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.023 on 196 degrees of freedom
## Multiple R-squared:  0.8972, Adjusted R-squared:  0.8956 
## F-statistic: 570.3 on 3 and 196 DF,  p-value: < 2.2e-16
## 
## 
## ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
## USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
## Level of Significance =  0.05 
## 
## Call:
##  gvlma(x = fit) 
## 
##                       Value   p-value                   Decision
## Global Stat        197.3907 0.000e+00 Assumptions NOT satisfied!
## Skewness            58.7289 1.810e-14 Assumptions NOT satisfied!
## Kurtosis            92.5125 0.000e+00 Assumptions NOT satisfied!
## Link Function       45.9814 1.194e-11 Assumptions NOT satisfied!
## Heteroscedasticity   0.1678 6.820e-01    Assumptions acceptable.

8.8 多重共線性（Multicollinearity）

多重共線性は VIF (variance inflation factor; 分散拡大要因) という指標で診断できます。
VIF は各説明変数に対して算出され、その値は 2 未満であることが望まれます。
VIF の値が 10 以上であれば、その変数は多重共線性の要因になっていることが示唆されます。

car::vif( fit )
##   youtube  facebook newspaper 
##  1.004611  1.144952  1.145187

vif( fit ) > 10 # 多重共線性の問題があるか
##   youtube  facebook newspaper 
##     FALSE     FALSE     FALSE

8.9 異常値

外れ値、高レバレッジ点、影響値などは回帰分析の結果に大きく影響するためよく検討しておく必要がある。

8.9.1 外れ値（Outliers）

目的変数の外れ値。

car::outlierTest( fit )
##      rstudent unadjusted p-value Bonferroni p
## 131 -5.757983          3.267e-08    6.534e-06

8.9.2 高レバレッジ点（High Leverage Point）

説明変数の外れ値。回帰直線へのレバレジ（影響力）が大きくなりやすい。

hat.plot = function( fit ) {
    p = length( coefficients(fit) )
    n = length( fitted(fit) )
    plot( hatvalues(fit), main = "Index Plot of Hat Values" )
    abline( h = c( 2, 3 ) * p / n, col = "red", lty = 2 )
    identify( 1:n, hatvalues(fit), names( hatvalues(fit) ) )
}

hat.plot( fit )
## integer(0)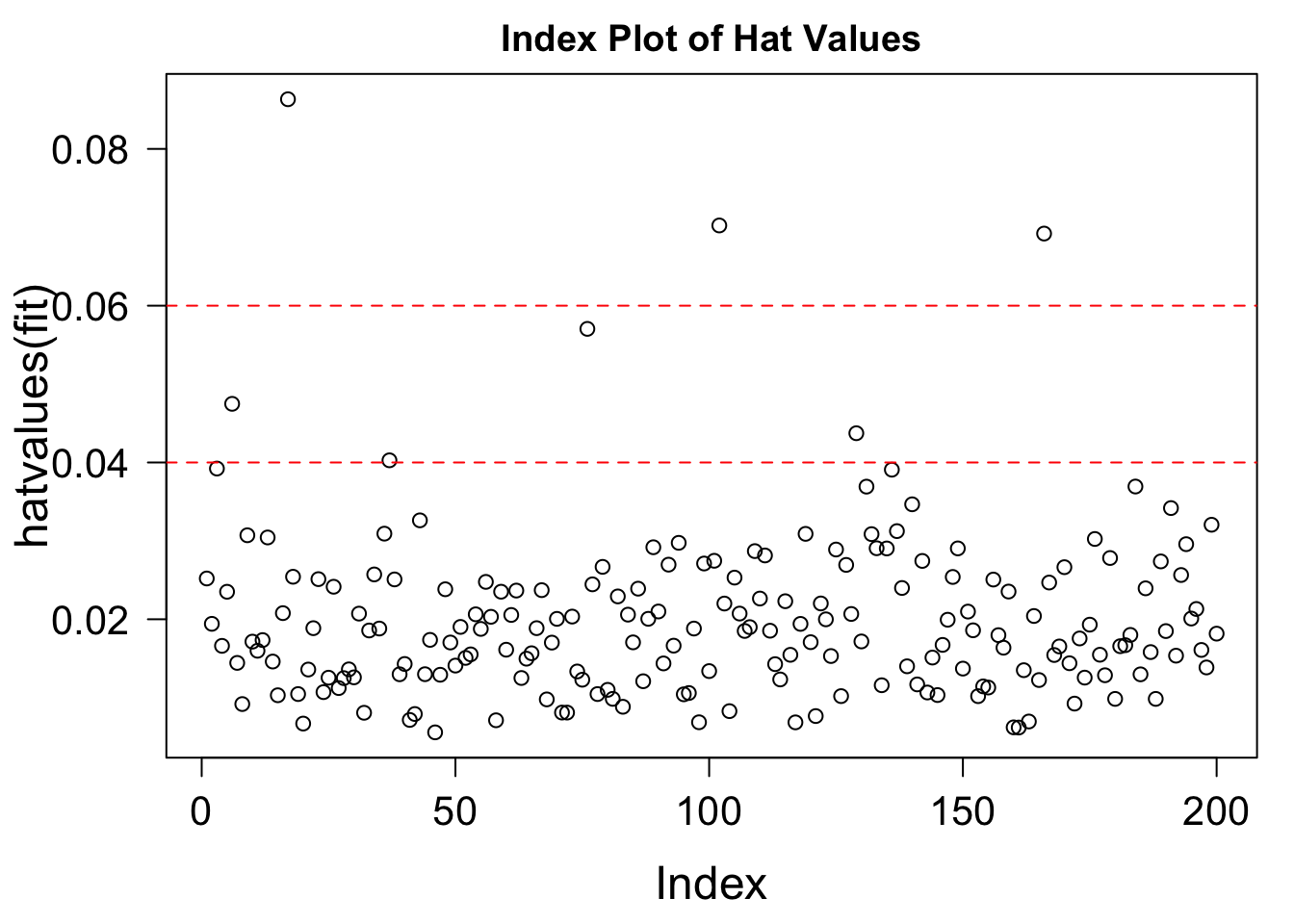

8.9.3 影響値（Influential observations）

クックの距離は、目的変数と説明変数の両方の外れ具合の指標。

cutoff = 4 / ( nrow(mkt) - length(fit$coefficients) - 2 )
par( mar = c( 6, 5, 2, 1 ) )
plot( fit, which = 4, cook.levels = cutoff )
abline( h = cutoff, lty = 2, col = "red" )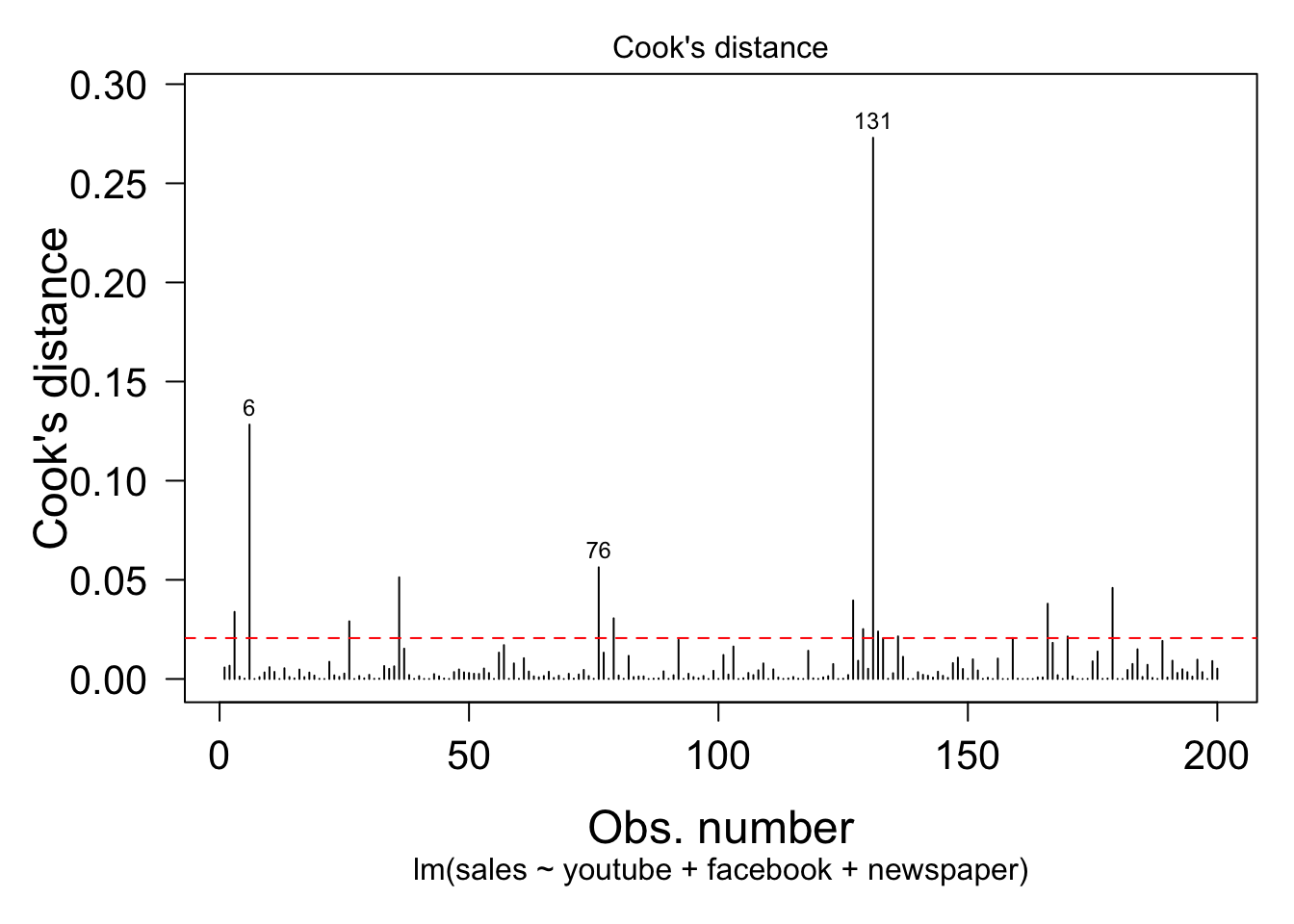

偏回帰 added-variable プロット（または偏回帰レバレッジ partial-regression leverage プロット）

avPlots( fit, ask = FALSE, id.method = "identify" )

影響プロット Influence plot

influencePlot( fit, id.method = "identify", main = "Influence Plot" )
##        StudRes        Hat        CookD
## 6   -3.2880331 0.04748107 0.1283058432
## 17  -0.2003981 0.08633414 0.0009533541
## 102  0.3422603 0.07023387 0.0022222175
## 131 -5.7579835 0.03691880 0.2729561213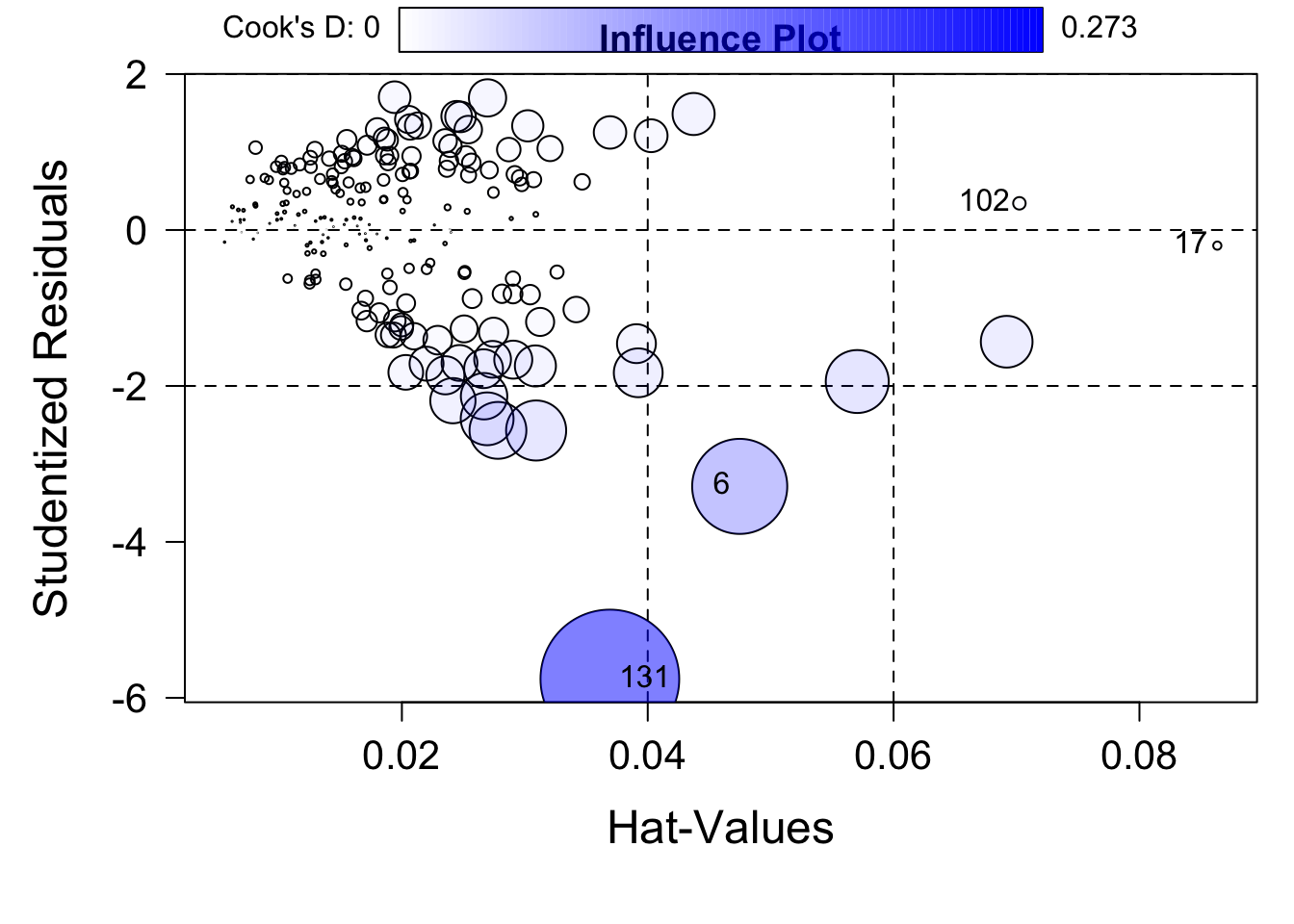

ハット値は説明変数の外れ具合
ステューデント化残差は目的変数の外れ具合
円の面積はクックの距離で、2つの外れ具合の両方を表す

8.10 対処方法

回帰モデルを診断して問題が見つかった場合にどのような対処をするか。

データの除外
変数変換
変数の追加または削除
異なる分析方法を用いる

といった方法が考えられます。

8.10.1 データの除外

外れ値や影響値を除外した上で回帰モデルのフィットを再度行います。
測定ミスや被験者が課題を正しく理解していなかったせいで生じた外れ値と考えられる場合はそのデータを除外することは正当ですが、そうでない場合には注意が必要。
モデルに合わないデータが存在する理由を考えることは現象についての洞察を得る機会になります。

8.10.2 変数変換

正規性・線形性・等分散性などが満たされない場合には変数を指数変換や対数変換すると状況が良くなる場合があります。

正規性や等分散性が満たされない場合には目的変数を変換することを試します。

car パッケージの powerTransform() 関数を使うとデータを最も正規分布に近づける指数の値を最尤推定します。

library( car )
summary( powerTransform( mkt$sales ) )
## bcPower Transformation to Normality 
##           Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
## mkt$sales    0.5779         0.5       0.3037       0.8521
## 
## Likelihood ratio test that transformation parameter is equal to 0
##  (log transformation)
##                            LRT df       pval
## LR test, lambda = (0) 20.53486  1 5.8555e-06
## 
## Likelihood ratio test that no transformation is needed
##                            LRT df      pval
## LR test, lambda = (1) 8.159602  1 0.0042834

結果の一番下で変数変換が不要という仮説が p < 0.05 で棄却されているので、何らかの変数変換が有用である（つまり変数変換した方が良さそう）であることがわかります。対数変換(Log transform)であるという仮説も p < 0.0 で棄却されているので、対数変換を使うべきではなさそうです。

Est Power が 0.5779 となっているので、sales 変数を約 0.6 乗することで sales 値の分布を正規分布に近づけることができます。この値は 0.5 に近いので平方根を使うのも良さそうです（X^0.5 = sqrt(X)なので）。

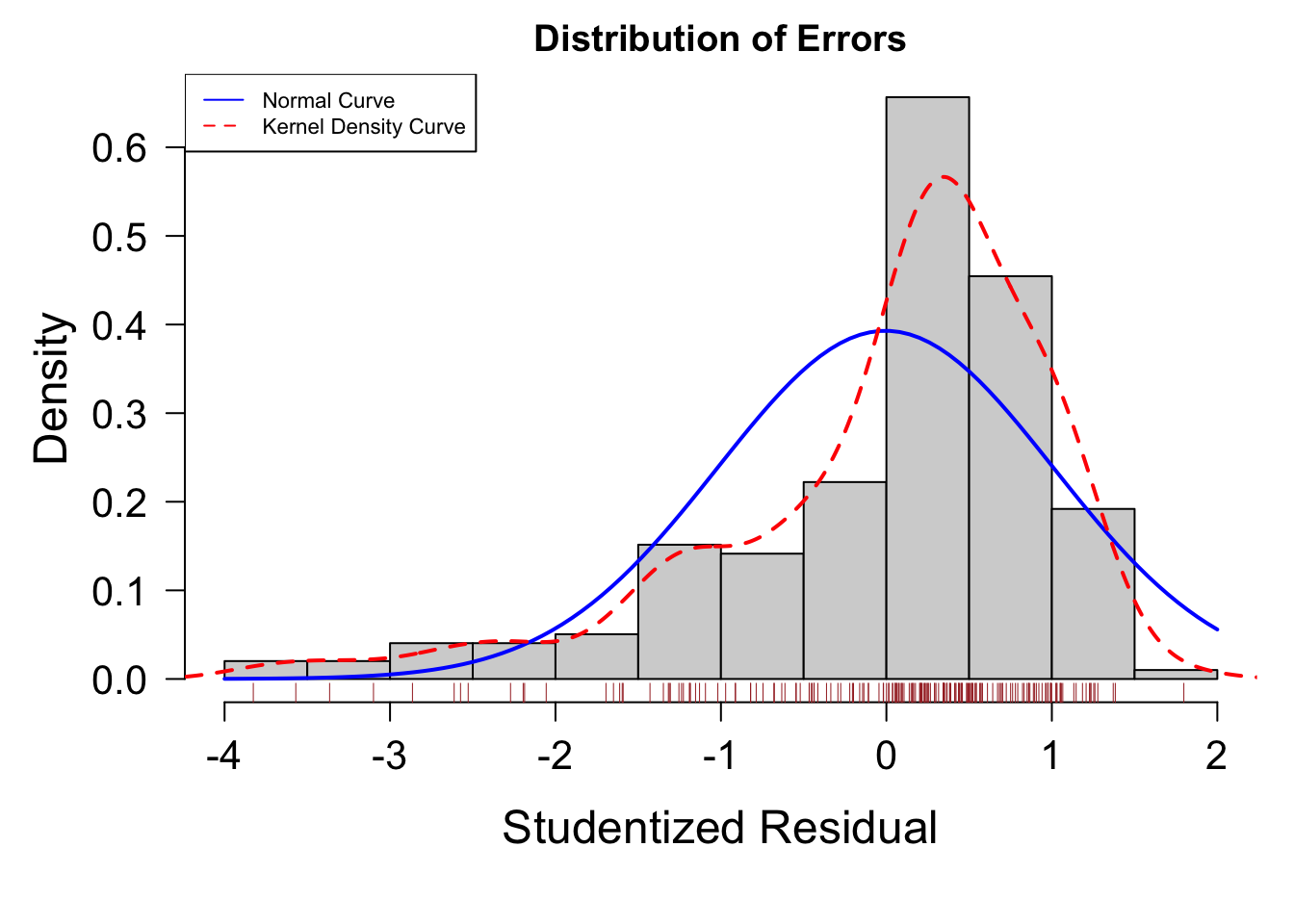
# 無変換
fit = lm( sales ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
residplot( fit )

# 指数変換
fit = lm( sales^0.6 ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
residplot( fit )

# 平方根変換
fit = lm( sqrt( sales ) ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
residplot( fit )

# 対数変換
fit = lm( log( sales ) ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
residplot( fit )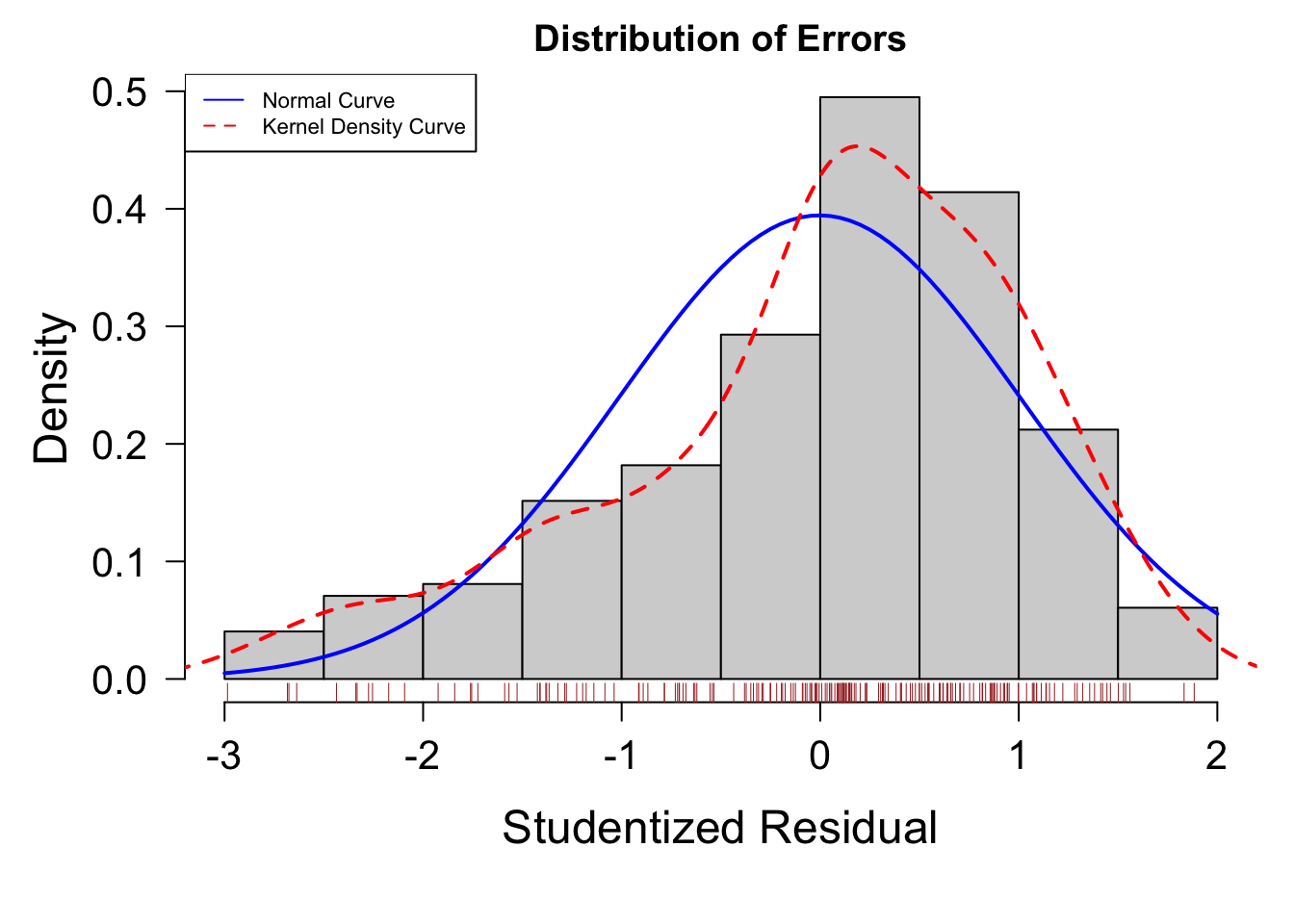

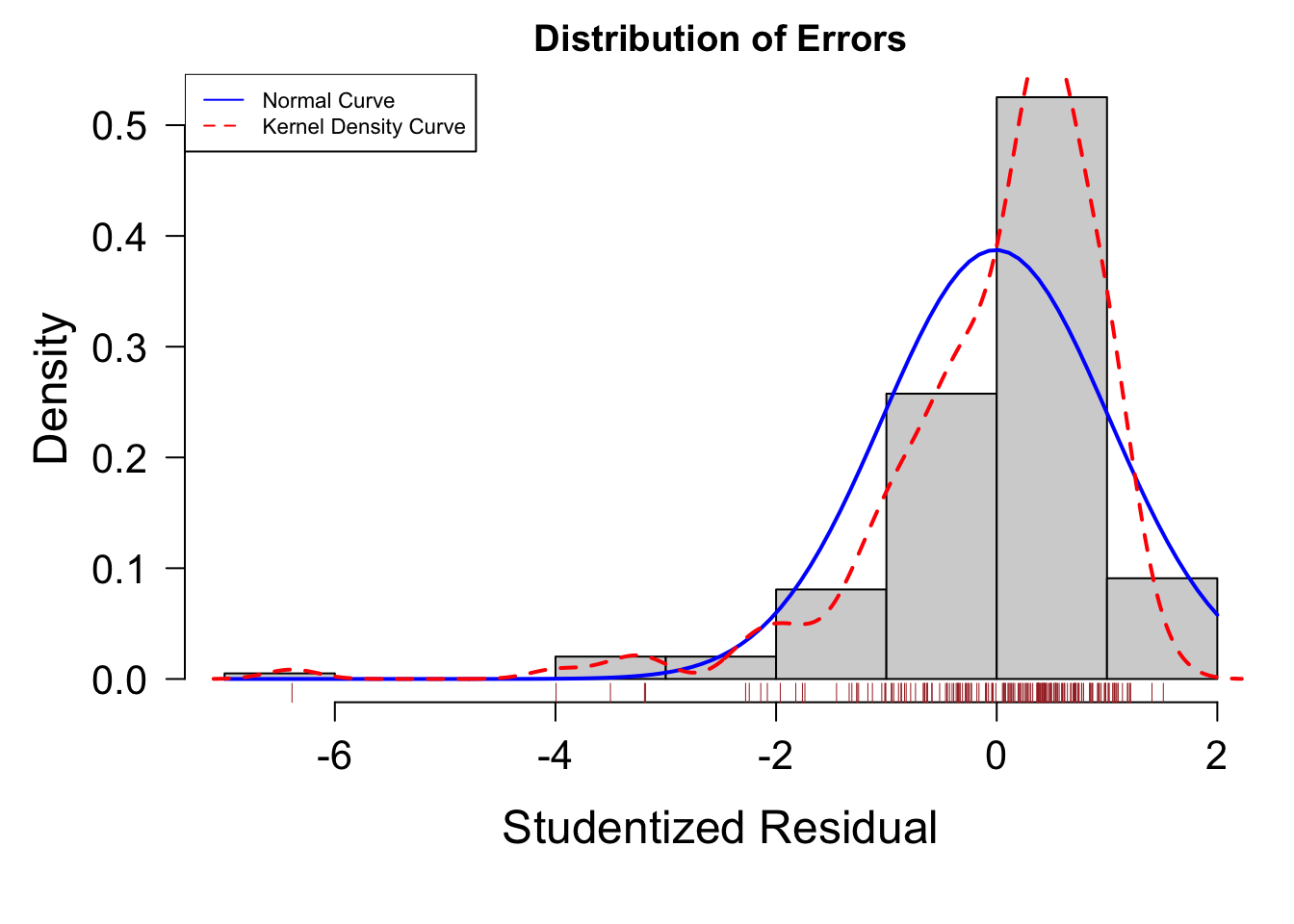
線形性が満たされない場合は説明変数を変数変換します。

car パッケージの boxTidwell() 関数は線形性を向上させる変換指数の最尤推定値を計算します。

boxTidwell 関数を使う際はデータの値が全て正の値(0もだめ)である必要があります。
marketing データの 128 行目の facebook の値が 0 なので、この行も除外して分析をします。

library( car )
boxTidwell( sales ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 128, 131 ), ] )
##           MLE of lambda Score Statistic (z)  Pr(>|z|)    
## youtube         0.47384             -7.1288 1.013e-12 ***
## facebook        1.17556              1.9016   0.05722 .  
## newspaper       6.22686             -0.2992   0.76481    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## iterations =  4

youtube は 0.47、facebook は 1.2、newspaper は 6.2 で指数変換すると良いことがわかります。ただし p < 0.05 であるのは youtube だけなので、youtube だけを変換すれば良いでしょう。

# 無変換のモデル
fit = lm( sales ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
summary(fit)$adj.r.squared
## [1] 0.913387

# youtube に平方根変換したモデル
fit = lm( sales ~ sqrt(youtube) + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
summary(fit)$adj.r.squared
## [1] 0.9337281

変数変換したモデルの方が R^2 値が大きいので、回帰モデルの当てはまりが良くなっています。

8.10.3 変数の追加または削除

特定の説明変数を分析から除外したり、新たな説明変数を追加したりすることで回帰モデルの当てはまりが良くなる場合があります。多重共線性が生じている場合は問題になっている変数を除外するのが良く使われる方法です。

8.10.4 異なる分析方法を用いる

一般化線形モデルなど他の分析方法を試す。

8.11 ベストな回帰モデルを選ぶ

8.11.1 AIC を用いた変数選択

AIC(赤池情報量規準)はモデルの予測性能の指標で、この値が小さいほど良いモデル(予測誤差が小さい)とされます。

fit1 = lm( sales ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
fit2 = lm( sales ~ youtube + facebook, data = mkt[ -c( 6, 131 ), ] )
fit3 = lm( sales ~ sqrt( youtube ) + facebook, data = mkt[ -c( 6, 131 ), ] )
AIC( fit1, fit2, fit3 )
##      df      AIC
## fit1  5 804.3332
## fit2  4 802.4814
## fit3  4 749.3737

fit3 が最も AIC の値が小さく、この 3 つのモデルの中では最良であると考えられます。

MASS パッケージの stepAIC() 関数を使うと変数を順に削除（または追加）していき、最も AIC が小さくなるモデルを探索します（ステップワイズ回帰）。

library( MASS )
fit = lm( sales ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
stepAIC( fit, direction = "backward" )
## Start:  AIC=240.43
## sales ~ youtube + facebook + newspaper
## 
##             Df Sum of Sq    RSS    AIC
## - newspaper  1       0.5  640.9 238.58
## <none>                    640.5 240.43
## - facebook   1    2082.9 2723.4 525.03
## - youtube    1    3985.9 4626.3 629.95
## 
## Step:  AIC=238.58
## sales ~ youtube + facebook
## 
##            Df Sum of Sq    RSS    AIC
## <none>                   640.9 238.58
## - facebook  1    2342.7 2983.6 541.10
## - youtube   1    3989.0 4629.9 628.10
## 
## Call:
## lm(formula = sales ~ youtube + facebook, data = mkt[-c(6, 131), 
##     ])
## 
## Coefficients:
## (Intercept)      youtube     facebook  
##     3.66229      0.04422      0.19529

ただし、この方法は常に最も良いモデルを見つけ出すとは限らない点に問題があります（あらゆる変数の組み合わせがチェックされるとは限らないので）。

8.11.2 All subsets regression

説明変数がそれほど多くない場合には、あらゆる変数の組み合わせについて回帰結果を比較する（全サブセット回帰）のが良いでしょう。

leaps パッケージの regsubsets() 関数を使うとそのような分析ができます。

library( leaps )
leaps = regsubsets( sales ~ youtube + facebook + newspaper,
    data = mkt[ -c( 6, 131 ), ], nbest = 3 )
plot( leaps, scale = "adjr2" )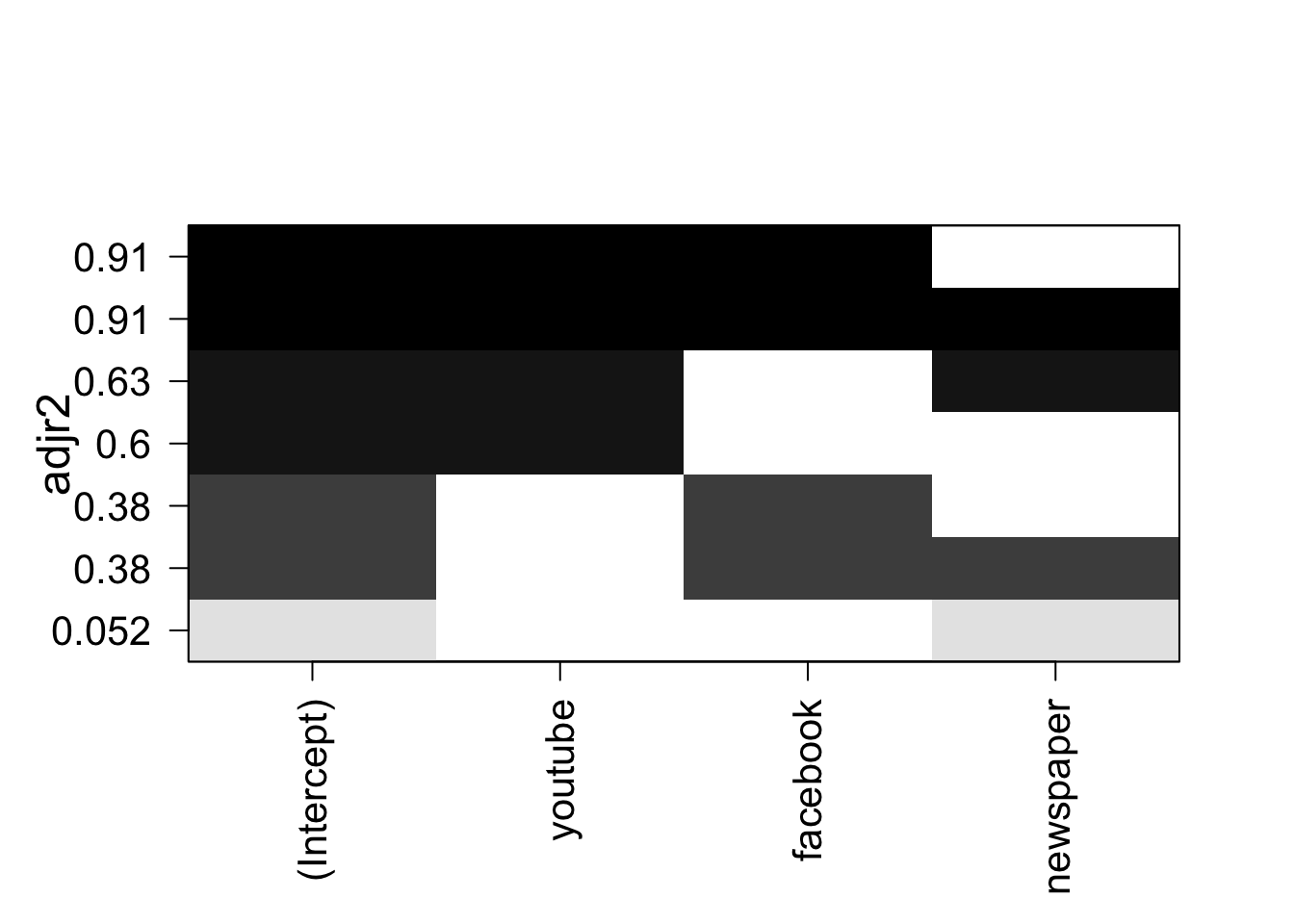

変数の組み合わせごとに回帰モデルの R^2 値が示されます。
youtube と facebook の 2 変数を使うモデルが最も良さそうとわかります。

8.12 交差検証（Cross validation）

交差検証はデータの一部のみを使ってモデルを作成し、残りのデータを使ってそのモデルの良さを評価する手法です。

library( bootstrap )

# 交差検証をする関数
getCrossVal = function( fit, k = 10 ){
    theta.fit = function( x, y ){ lsfit( x, y ) }
    theta.predict = function( fit, x ){ cbind( 1, x ) %*% fit$coef }
    x = fit$model[ , 2:ncol( fit$model ) ]
    y = fit$model[ , 1 ]
    results = crossval( x, y, theta.fit, theta.predict, ngroup = k )
    return( results )
}

fit = lm( sales ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )
r2 = cor( fit$model[,1], fit$fitted.values )^2

k = 10
results = getCrossVal( fit, k )
r2cv = cor( fit$model[,1], results$cv.fit )^2

print( r2 ) # 元のR2乗値
## [1] 0.914706
print( r2cv ) # 交差検証した場合のR2乗値
## [1] 0.9111286

8.13 標準化回帰係数

回帰モデルの各説明変数間の相対的な重要性を知るには、説明変数の標準化回帰係数を見るのが簡単な方法です。
データの各説明変数の値を z 変換した上で回帰分析をすれば標準化回帰係数が得られます。

z = as.data.frame( scale( mkt[ -c( 6, 131 ), ] ) )
fit = lm( sales ~ youtube + facebook + newspaper, data = z )
options( scipen = 10 )
coef( fit )
##   (Intercept)       youtube      facebook     newspaper 
## -4.958047e-17  7.315642e-01  5.633386e-01 -8.537919e-03

標準化回帰係数は youtube の 0.73 が最も大きな値です。
youtube の値が 1 標準偏差増えると sales が 0.73 標準偏差増えることを意味します。
売り上げの予測に最も重要な説明変数は youtube であることがわかります。

8.14 相対的重みづけ分析

各説明変数間の相対的な重要性を定量化するには他にも様々な方法が提案されています。
相対的重みづけ（relative weights）は当該説明変数をモデルに加えた時のR^2値の増加の期待値として計算されます。
https://www.researchgate.net/publication/220030359

relweights <- function( fit ){
    R = cor( fit$model )
    nvar = ncol( R )
    svd = eigen( R[ 2:nvar, 2:nvar ] )
    evec = svd$vectors
    delta = diag( sqrt( svd$values ) )
    lambda = evec %*% delta %*% t( evec )
    beta = solve( lambda ) %*% R[ 2:nvar, 1 ]
    rawwgt = lambda^2 %*% beta^2
    import = (rawwgt / colSums( beta^2 ) ) * 100
    import = as.data.frame( import )
    row.names(import) = names( fit$model[ 2:nvar ] )
    names( import ) = "Weights"
    import = import[ order( import ), 1, drop = F ]
    return( import )
}

fit = lm( sales ~ youtube + facebook + newspaper, data = mkt[ -c( 6, 131 ), ] )

relweights( fit )
##            Weights
## newspaper  2.57958
## facebook  35.72230
## youtube   61.69812

この結果は、回帰モデルのR^2値のうちの 61% を youtube が説明し、35%を facebook が説明することを意味します。この分析結果からも、youtube が最も重要な説明変数であることがわかります。

8.15 練習問題

新たなデータを題材にして、（重）回帰分析の練習をしてみましょう。

8.15.1 データについて

Atir らが 2015年に Psychological Science 誌に発表した論文のデータを用います。
今回の分析で用いるのはこの論文の中の Study 1b のものです。

この論文では overclaiming と呼ばれる現象について研究を行なっています。
overclaiming とは、知っているはずのない事柄に対して、それを知っていると主張することです。
例えば、「事前相場株式」について知っているかと聞かれて、知っていると答えた場合、それは overclaiming です（「事前相場株式」という言葉は存在しません）。

overclaiming がなぜ起こるのかを調べるため、Study 1b では 202名の被験者を集めて質問紙調査を行いました。被験者らは、(A) 金融に関して自分がどれほど知識が豊富だと思うかを調べる質問紙と、(B) 金融に関する様々な単語についてそれを知っている度合いを調べる質問紙に回答しました。どちらの質問紙を先に回答するかはカウンターバランスされました。質問紙 B は 15 個の金融用語それぞれについて、知っている度合いを 7 段階で評定するものでした。ただし、15個のうち3個は実在しない架空の用語でした。

論文では、自分の知識豊富さに関する自覚が overclaiming にどう影響するかについて、重回帰分析を用いた分析結果が報告されています。

論文:
Atir, S., Rosenzweig, E., & Dunning, D. (2015). When knowledge knows no bounds: Self-perceived expertise predicts claims of impossible knowledge. Psychological Science, 26, 1295-1303.

論文リンク

参考ページ:
https://sites.trinity.edu/osl/data-sets-and-activities/regression-activities

8.15.2 データの読み込み

dat = read.table( file = "http://htsuda.net/stats/dataset/overclaiming.csv",
    header=T, sep = ",", stringsAsFactors = F )
head( dat )
##   id overclaiming confidence    accuracy FINRA order
## 1  1    0.4444444        5.5  0.25000000     4     1
## 2  7    0.5555556        4.5  0.19444444     4     1
## 3 10    0.1666667        3.5  0.34722222     5     1
## 4 12    0.7222222        6.0 -0.05555556     4     1
## 5 14    0.3888889        2.5  0.16666667     3     1
## 6 17    0.9444444        7.0 -0.04166667     4     1

各列の内容は以下の通り：

id: 被験者番号
overclaiming: 質問紙 B (overclaiming task)で、実在しない金融用語を知っていると回答した度合い
confidence: 質問紙 A (self-perceived knowledge of personal finance) のスコア
accuracy: 質問紙 B の正解率
FINRA: FINRA 質問紙のスコア
order: overclaiming 課題と confidence 課題を行なった順番

8.15.3 分析したいこと

overclaiming の平均や分散、分布（ヒストグラム）を調べる。
confidence と overclaiming の関係を調べる。
confidence と overclaiming の関係は、accuracy や FINRA の影響を統制した上でもなお見られるか。
課題順序の影響はあるか。

8.15.4 分析

グラフ化

まずは横軸に confidence、縦軸に overclaiming をとってグラフにしてみます。

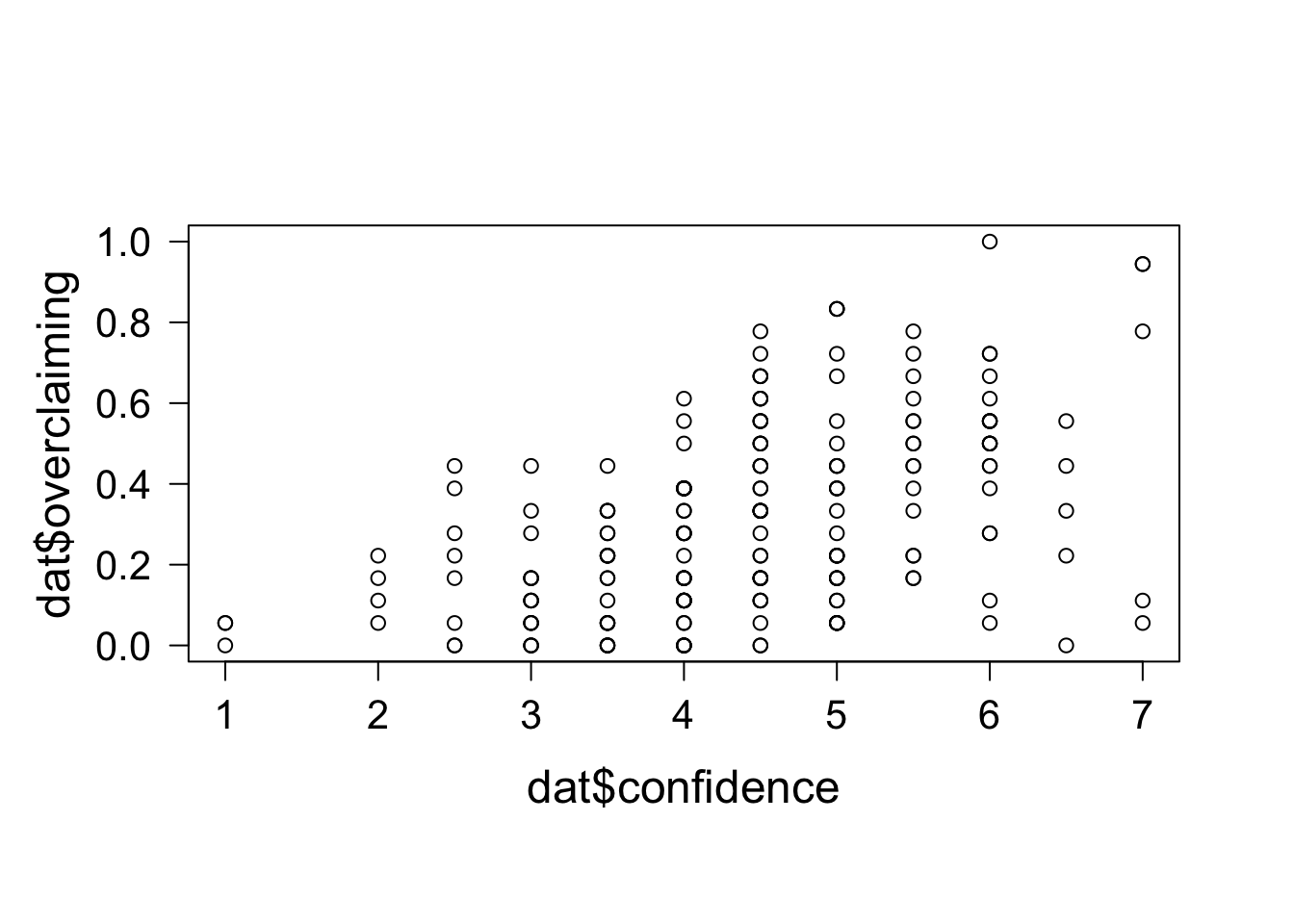
plot( dat$confidence, dat$overclaiming )

正の相関がありそうです。

car パッケージの関数を使って他の変数との関係もまとめて図示してみます。
被験者番号は図に含める必要がないので、sebset 関数を使って id の列を除外しています。

library( car )
scatterplotMatrix( subset( dat,select = -id ),
    regLine = list( col = "#2792b3", lwd = 3 ), col = "black", cex = .5 )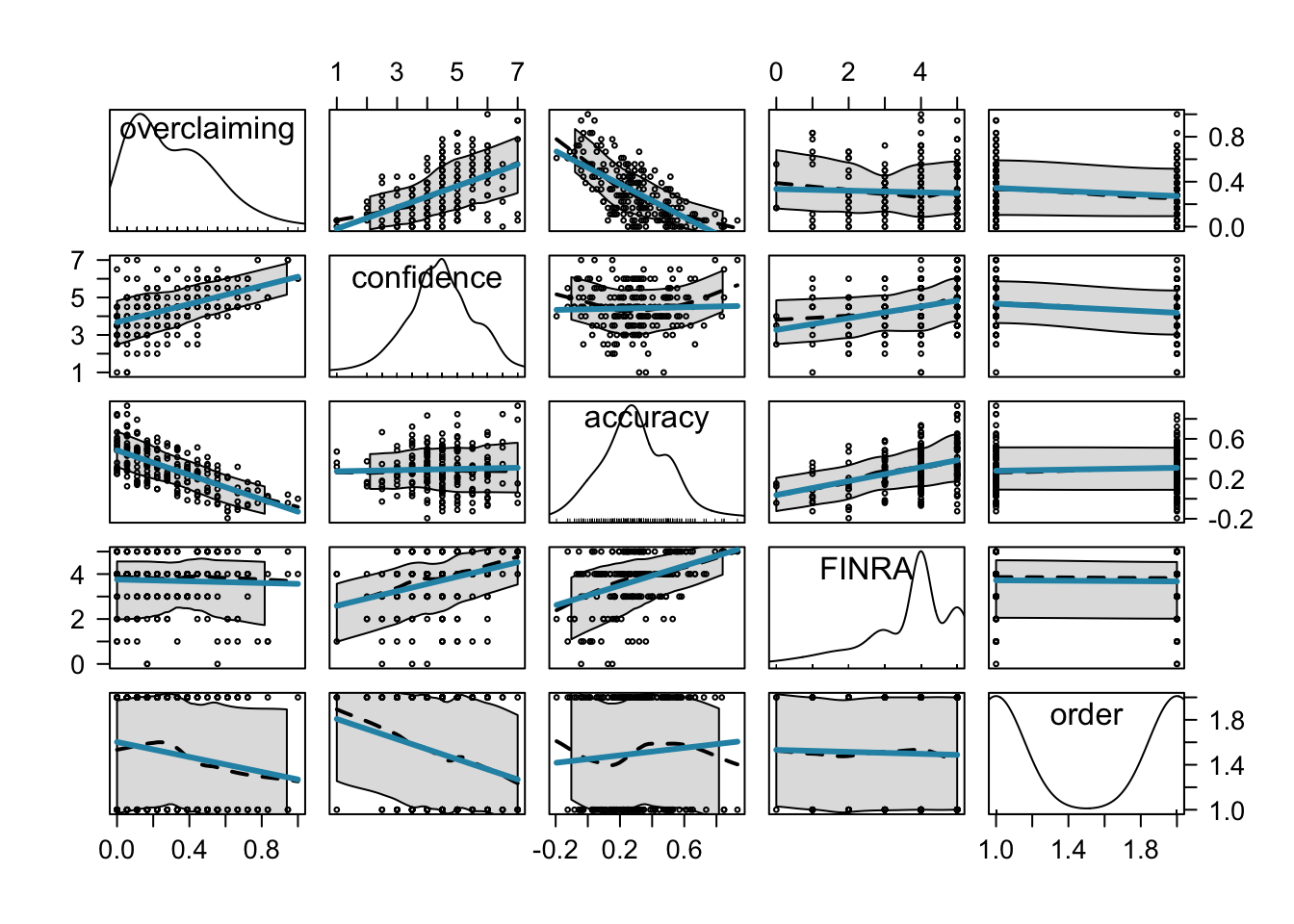

Accuracy が overclaiming と負の相関を持っていそうなことや、order が overclaiming や confidence と負の相関を持っていそうなことなどが推察できます。

8.15.4.1 回帰分析の実施

では回帰分析を実施しましょう。

論文のページ 3 に結果が記載されています。
Study 1a についての記述の部分で

“We next entered self-perceived knowledge of personal finance (M = 4.23, SD = 1.22) and accuracy into a regression model predicting overclaiming”.

とあるように、self-perceived knowledge of personal finance (confidence のこと) と acuracy を用いて overclaiming を予測する回帰モデルによる分析をしていることがわかります。

実験 1b のその分析結果は以下のように書かれています。

“Likewise, in Study 1b, self-perceived knowledge of personal finance (M = 4.43, SD = 1.17) positively predicted overclaiming, b = 0.10, t(199) = 13.07, p < .001.”

この分析結果を再現してみましょう。

fit = lm( overclaiming ~ confidence + accuracy, data = dat )
summary( fit )
## 
## Call:
## lm(formula = overclaiming ~ confidence + accuracy, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.37190 -0.09280 -0.00796  0.09369  0.31250 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.088910   0.036737    2.42   0.0164 *  
## confidence   0.099765   0.007632   13.07   <2e-16 ***
## accuracy    -0.753986   0.042195  -17.87   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1268 on 199 degrees of freedom
## Multiple R-squared:  0.7049, Adjusted R-squared:  0.702 
## F-statistic: 237.7 on 2 and 199 DF,  p-value: < 2.2e-16

confidence の行の結果を見ると、b = 0.099765、t = 13.07, p < 2e-16 となっています。
b は四捨五入すれば 0.10 なので、論文中での値と同じ値が得られました。

（ちなみに、p 値の 2e-16 という値は相関係数の検定の Notes でも補足したように、使っているコンピュータで扱える最小の数値ですので、「とにかく小さな数」という以上の意味はありません）

次に、質問紙の回答順序の効果に関して次のような記述があります。

“overclaiming was higher when self-perceived knowledge was assessed first (M = 0.34, SD = 0.24) rather than second (M = 0.27, SD = 0.21), t(200) = 2.21, p < .05.”

どうやら、self-perceived knowledge (confidence) を先に回答したグループの方が overclaiming が多かったようです。

この結果を再現してみましょう。データを order の値が 1 のグループと 2 のグループに分けて、両グループの overclaiming の値について、対応なしの t 検定をします。

order1 = subset( dat, order == 1 )
order2 = subset( dat, order == 2 )
t.test( x = order1$overclaiming, y = order2$overclaiming, paired = F )
## 
##  Welch Two Sample t-test
## 
## data:  order1$overclaiming and order2$overclaiming
## t = 2.2092, df = 196.3, p-value = 0.02832
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.007673654 0.135340648
## sample estimates:
## mean of x mean of y 
## 0.3437844 0.2722772

結果の一番下に平均値が表示されており、論文中の M = 0.34 と M = 0.27 と合っています。
t = 2.2092, p = 0.02832 で、これも論文中の値と合っていますね。

この結果から、質問紙の回答順序によって overclaiming の度合いに違いがあったとわかります。ただし、どちらの順でやったにせよ confidence と overclaiming の関係は有意であったようです。そのことが以下のように書かれています。

“However, self-perceived knowledge significantly predicted overclaiming regardless of whether it was assessed before the overclaiming task, b = 0.12, t(98) = 9.83, p < .001, or after it, b = 0.09, t(98) = 8.47, p < .001.”

この結果を再現してみましょう。

fit1 = lm( overclaiming ~ confidence + accuracy, data = order1 )
summary( fit1 )$coefficients
##                Estimate Std. Error     t value     Pr(>|t|)
## (Intercept)  0.03212968 0.05786849   0.5552189 5.800101e-01
## confidence   0.11609056 0.01181235   9.8278994 2.860539e-16
## accuracy    -0.82337851 0.06176005 -13.3318948 9.634900e-24

fit2 = lm( overclaiming ~ confidence + accuracy, data = order2 )
summary( fit2 )$coefficients
##                Estimate Std. Error    t value     Pr(>|t|)
## (Intercept)  0.12563975 0.04749031   2.645587 9.500232e-03
## confidence   0.08625226 0.01018405   8.469347 2.502806e-13
## accuracy    -0.69035725 0.05709228 -12.091954 3.827786e-21

（summary の結果のうち回帰係数の部分のみを表示させています）

order が 1（confidence の質問紙が先）の時は b = 0.11609, t = 9.828, p = 2.86e-16、
order が 2 の時は b = 0.08625, t = 8.469, p = 2.502806e-13
となっており、論文中の値と一致しています。

続いて以下の記述を確認します。

“Genuine knowledge, as assessed by the financial literacy quiz, also positively predicted overclaiming, b = 0.05, t(199) = 4.92, p < .001. Selfperceived knowledge was positively correlated with genuine knowledge, r(200) = .32, p < .001.”

前半に関しては以下のような回帰モデルを作ると論文中の数値と一致しました。

fit = lm( overclaiming ~ accuracy + FINRA, data = dat )
summary( fit )$coefficients
##                Estimate Std. Error    t value     Pr(>|t|)
## (Intercept)  0.36753508 0.03763551   9.765645 1.184693e-18
## accuracy    -0.84939256 0.05896567 -14.404866 1.072211e-32
## FINRA        0.05173864 0.01050767   4.923892 1.778199e-06

後半の相関に関しては

cor.test( dat$confidence, dat$FINRA )
## 
##  Pearson's product-moment correlation
## 
## data:  dat$confidence and dat$FINRA
## t = 4.7414, df = 200, p-value = 0.000004027
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.1880809 0.4367626
## sample estimates:
##       cor 
## 0.3178783

で同じ結果になることが確認できます。

次の段落で、最後の分析として、genuine knowledge (FINRA スコアのこと) を含めた回帰分析が報告されています。

“When genuine knowledge was entered into the model with self-perceived knowledge, self-perceived knowledge remained a highly significant predictor of overclaiming, b = 0.09, t(198) = 11.73, p < .001.”

order 以外のすべての要因を回帰モデルに入れれば良いので、

fit = lm( overclaiming ~ confidence + accuracy + FINRA, data = dat )
summary( fit )$coefficients
##                Estimate  Std. Error    t value     Pr(>|t|)
## (Intercept)  0.05778680 0.039202720   1.474051 1.420560e-01
## confidence   0.09406917 0.008018126  11.732064 1.785419e-24
## accuracy    -0.79321893 0.045655133 -17.374146 1.109049e-41
## FINRA        0.01836965 0.008576246   2.141922 3.342126e-02

これで論文と同じ結果が得られます。
accuracy や FINRA の影響を統制した上でもなお overclaiming と confidence には有意な関係がありました。

回帰モデルの診断

論文中の結果の記述は以上ですが、ここでは続けて回帰モデルの診断基準についての分析もしておきましよう。

正規性を Q-Q プロットで確認します。
データが直線的に並んでいるので、正規性が満たされていることが確認できます。

library( car )

fit = lm( overclaiming ~ confidence + accuracy + FINRA, data = dat )
qqPlot( fit, labels = row.names( dat ), id.method = "identity", simulate = T )
## [1] 21 67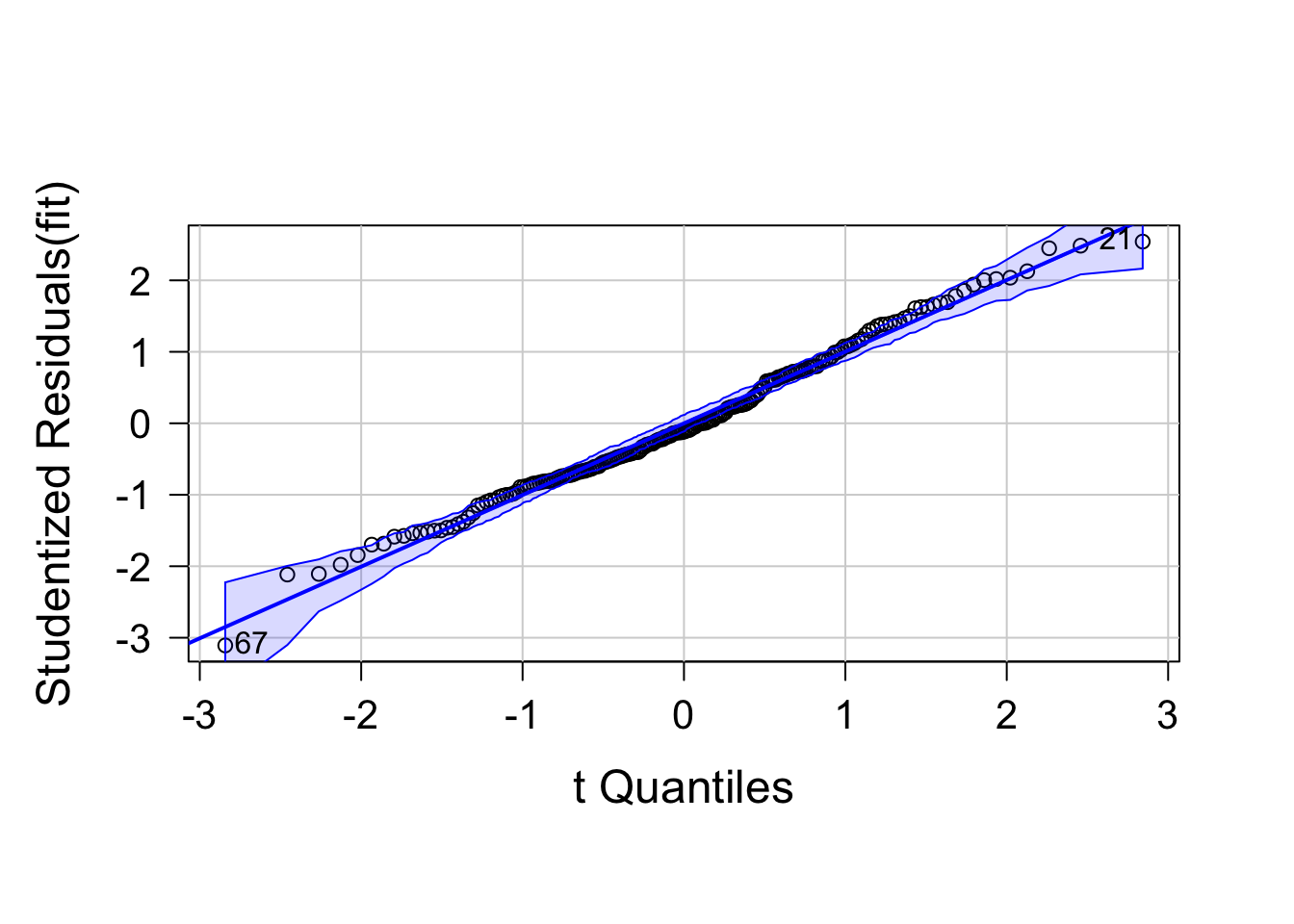

次に線形性を見ます。
青の点線は直線を当てはめたもので、紫の実線はデータにひっつく曲線（Loes）です。
紫（データ）は青の直線上に並んでいるので、説明変数と目的変数に直線的な関係がある（つまり線形性が満たされる）ことが確認できます。

car::crPlots( fit )

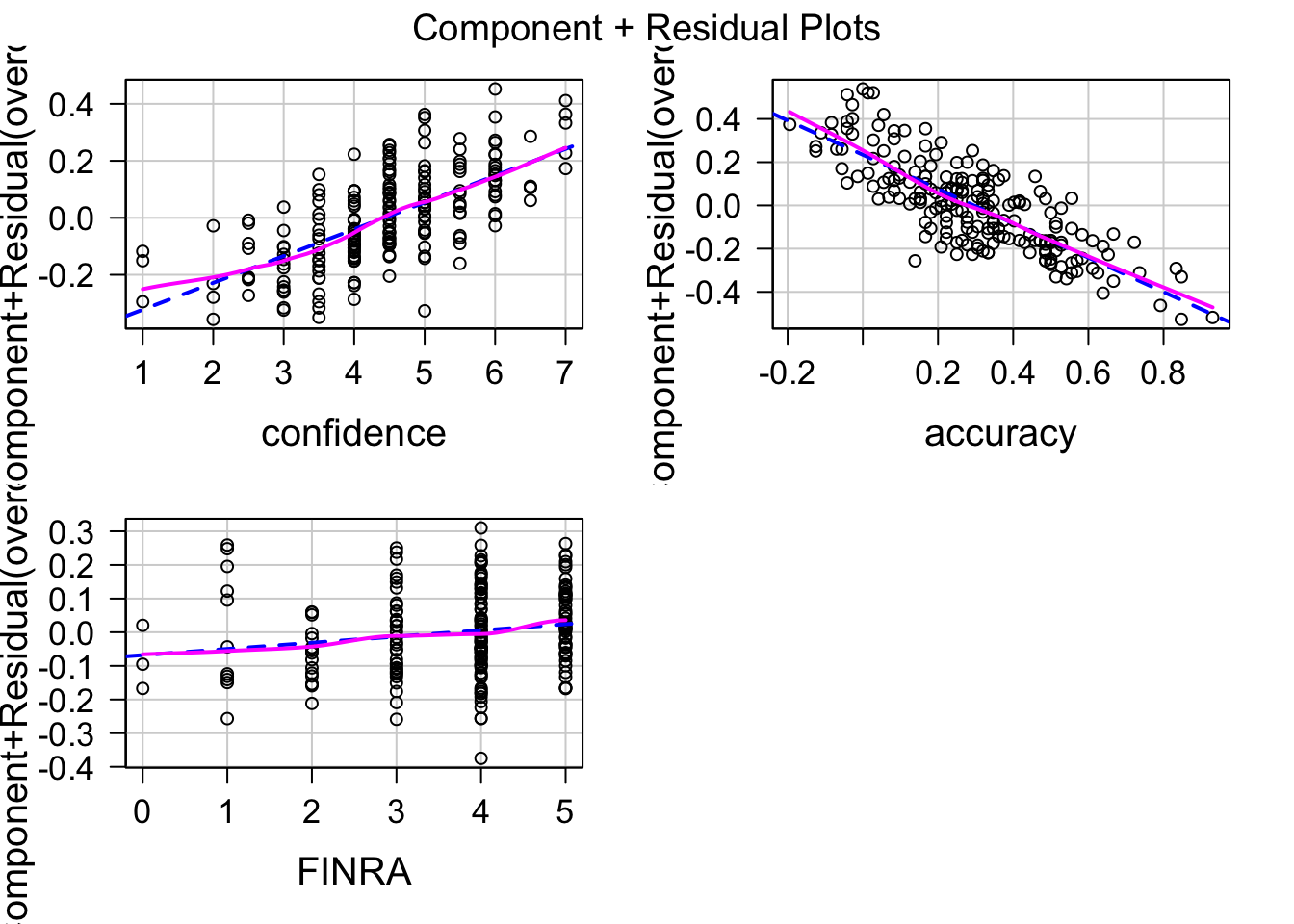
次に等分散性を確認します。

car::ncvTest( fit )
## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 2.789667, Df = 1, p = 0.094874

spreadLevelPlot( fit )
## 
## Suggested power transformation:  0.7769507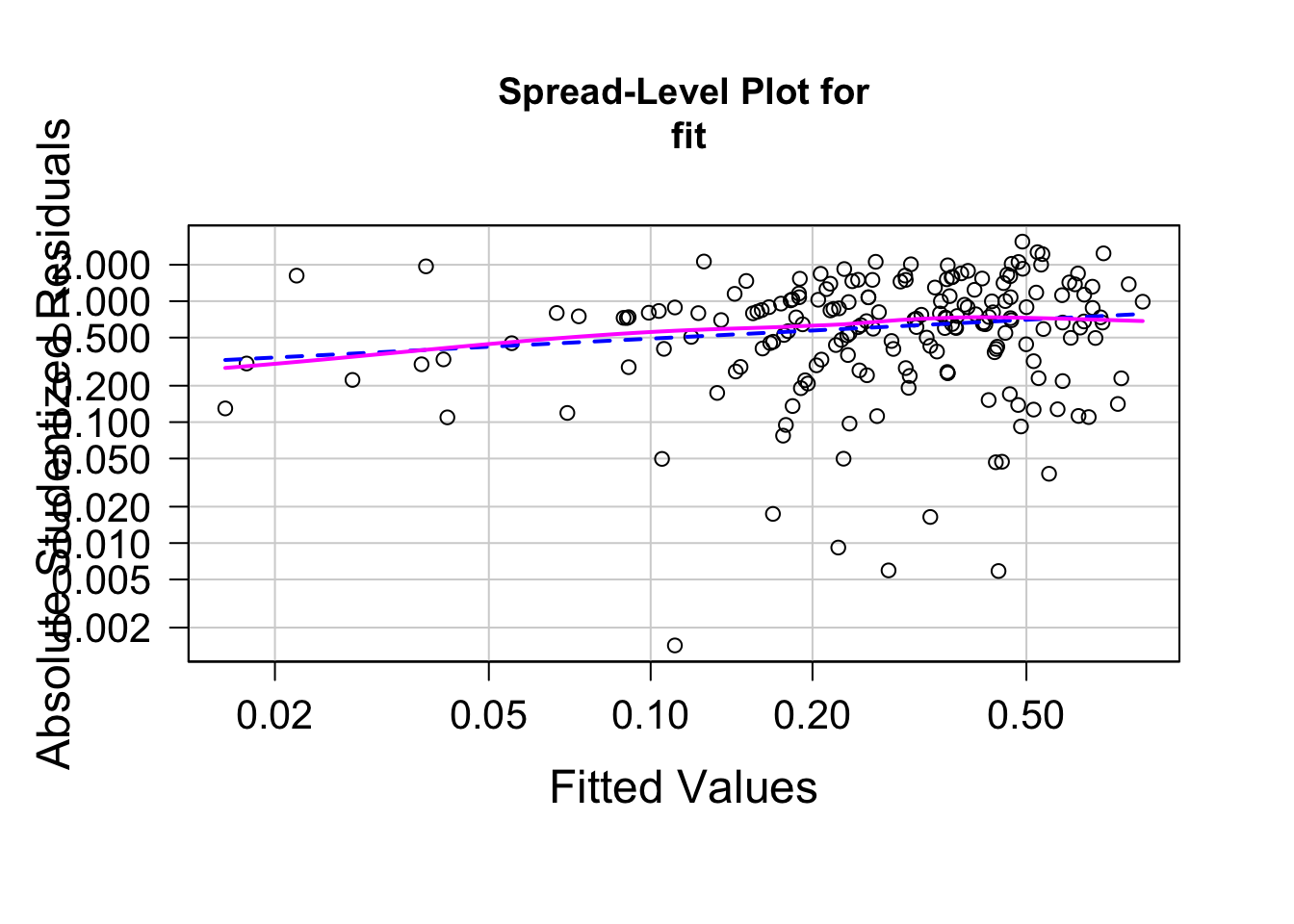

p = 0.09 なので、等分散であるという帰無仮説は棄却されず、分散に差があるとは言えない、という結果です。図を見ると、残差は少し右上がりではありますがほぼ水平になっているので、等分散であることを示唆します。

最後に多重共線性をチェックします。

car::vif( fit )
## confidence   accuracy      FINRA 
##   1.124776   1.193106   1.325805

どの説明変数についても値は 2 未満であるので、多重共線性の問題はないことが確認できました。