10 テスト課題
回帰分析と因子分析それぞれについて、分析結果を「解答例」のような文章にし、メールで提出して下さい。
回帰分析
読解能力に関するデータを用いて重回帰分析をして下さい。
データについて
これは 40 行 4 列のデータで、40 人分の生徒について age（年齢）、memory（短期記憶容量の測定値）、IQ（IQの測定値）、reading（読解能力のスコア）という4つの値があります。
分析すること
散布図などの図を描いてデータの分布を視覚的に確認する。
reading を目的変数とし、age・memory・IQ を説明変数とした重回帰分析をする。
説明変数同士の交互作用も検討する。
解答例
読解能力を目的変数とし、年齢・短期記憶容量・IQ を説明変数とする重回帰分析を行なった。〜は読解能力と［正・負］の相関があった（偏相関係数 = 〜、t値 = 〜、p値 = 〜）。回帰モデルに〜と〜の交互作用項を加えたところ、〜という結果であった。
分析手続き
まずは散布図を描いてデータの分布を視覚的に確認しておきます。
library( car )
scatterplotMatrix( dat, spread = F, smooth = F,
regLine = list( col = "#2792b3", lwd = 3 ), col = "black", cex = .5 )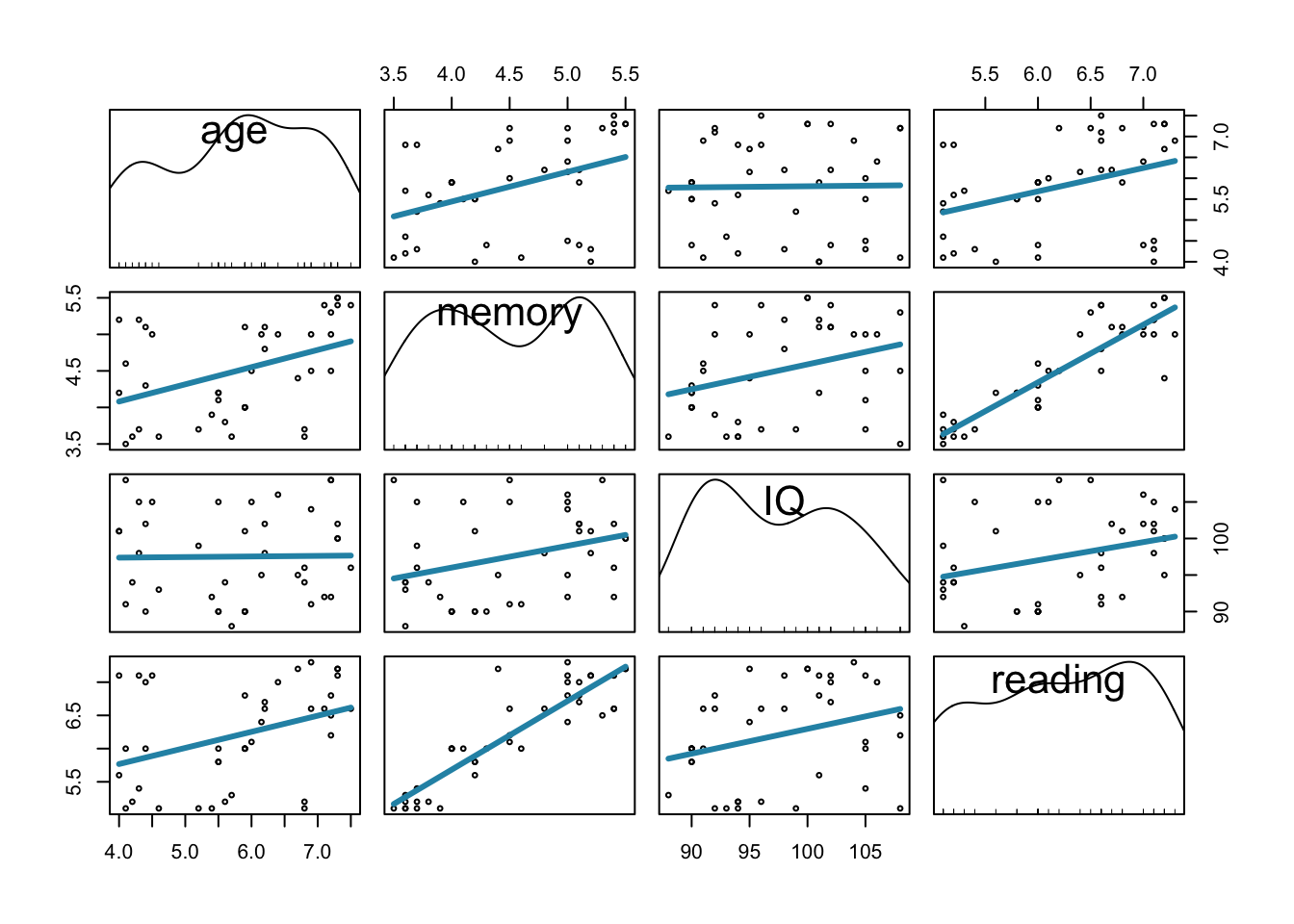
記憶と読解力に相関が相関し、記憶と年齢にも相関がありそうだと分かります。
次に重回帰分析をします。
fit = lm( reading ~ age + memory + IQ, data = dat )
summary( fit )
##
## Call:
## lm(formula = reading ~ age + memory + IQ, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.54727 -0.17157 -0.03313 0.17790 1.10765
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.342529 0.894790 1.500 0.142
## age 0.001245 0.052074 0.024 0.981
## memory 1.025408 0.095501 10.737 8.98e-13 ***
## IQ 0.002418 0.009326 0.259 0.797
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3347 on 36 degrees of freedom
## Multiple R-squared: 0.8158, Adjusted R-squared: 0.8005
## F-statistic: 53.15 on 3 and 36 DF, p-value: 2.645e-13
vif( fit )
## age memory IQ
## 1.222940 1.360908 1.133255記憶のみに有意な効果が見られました。
VIF の値は 2 未満であるので、多重共線性の問題はありません。
次に交互作用も加えた分析をしてみます。
memory だけ残して age と IQ は外し、交互作用項を加えた式で重回帰します。
fit = lm( reading ~ memory + memory:age + memory:IQ + age:IQ, data = dat )
summary( fit )
##
## Call:
## lm(formula = reading ~ memory + memory:age + memory:IQ + age:IQ,
## data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.52004 -0.24495 0.04774 0.12964 1.06148
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.555795 1.994032 -0.780 0.4405
## memory 2.330621 0.887064 2.627 0.0127 *
## memory:age -0.120635 0.074633 -1.616 0.1150
## memory:IQ -0.006312 0.004855 -1.300 0.2021
## age:IQ 0.005710 0.003590 1.591 0.1207
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3272 on 35 degrees of freedom
## Multiple R-squared: 0.8289, Adjusted R-squared: 0.8093
## F-statistic: 42.38 on 4 and 35 DF, p-value: 5.935e-13
vif( fit )
## memory memory:age memory:IQ age:IQ
## 122.87209 120.88675 51.25307 66.24142記憶のみ有意で、交互作用はどれも効果が認められませんでした。
VIF の値が大きいので多重共線性が原因となっている可能性があります。
ただし、
library( leaps )
leaps = regsubsets( reading ~ memory + memory:age + memory:IQ + age:IQ,
data = dat, nbest = 3 )
plot( leaps, scale = "adjr2" )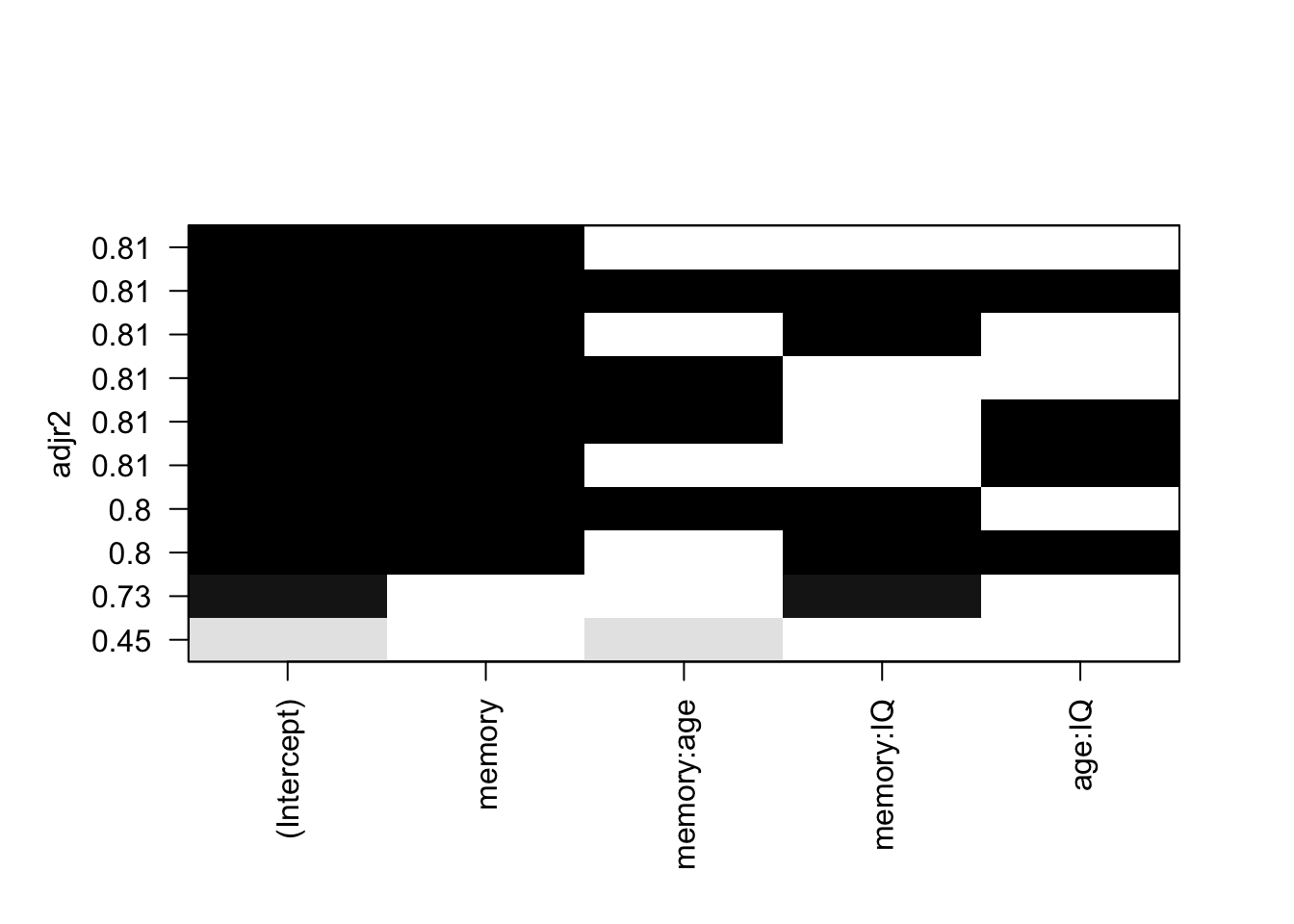
この結果から、記憶の他に交互作用項を回帰モデルに加えても R2乗値は増えないので、今回のデータの場合には交互作用については考える必要は無いと判断できます。
［補足］age と memory だけを使って分析すると交互作用が有意になります。
reading ~ age * memory は
reading ~ age + memory + age:memory と同じ意味です。
fit = lm( reading ~ age * memory, data = dat )
summary( fit )
##
## Call:
## lm(formula = reading ~ age * memory, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.47998 -0.21439 0.00576 0.18797 1.02185
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.49209 1.87199 -1.331 0.1915
## age 0.70669 0.32461 2.177 0.0361 *
## memory 1.90897 0.40598 4.702 3.72e-05 ***
## age:memory -0.15143 0.06872 -2.203 0.0340 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3145 on 36 degrees of freedom
## Multiple R-squared: 0.8374, Adjusted R-squared: 0.8238
## F-statistic: 61.8 on 3 and 36 DF, p-value: 2.839e-14
vif( fit )
## age memory age:memory
## 53.83049 27.85850 110.94282交互作用について可視化してみると、
fit = lm( reading ~ age * memory, data = dat )
library( effects )
plot( effect( "age:memory", fit, xlevels = list( age = c(5,6,7) ) ), multiline = T )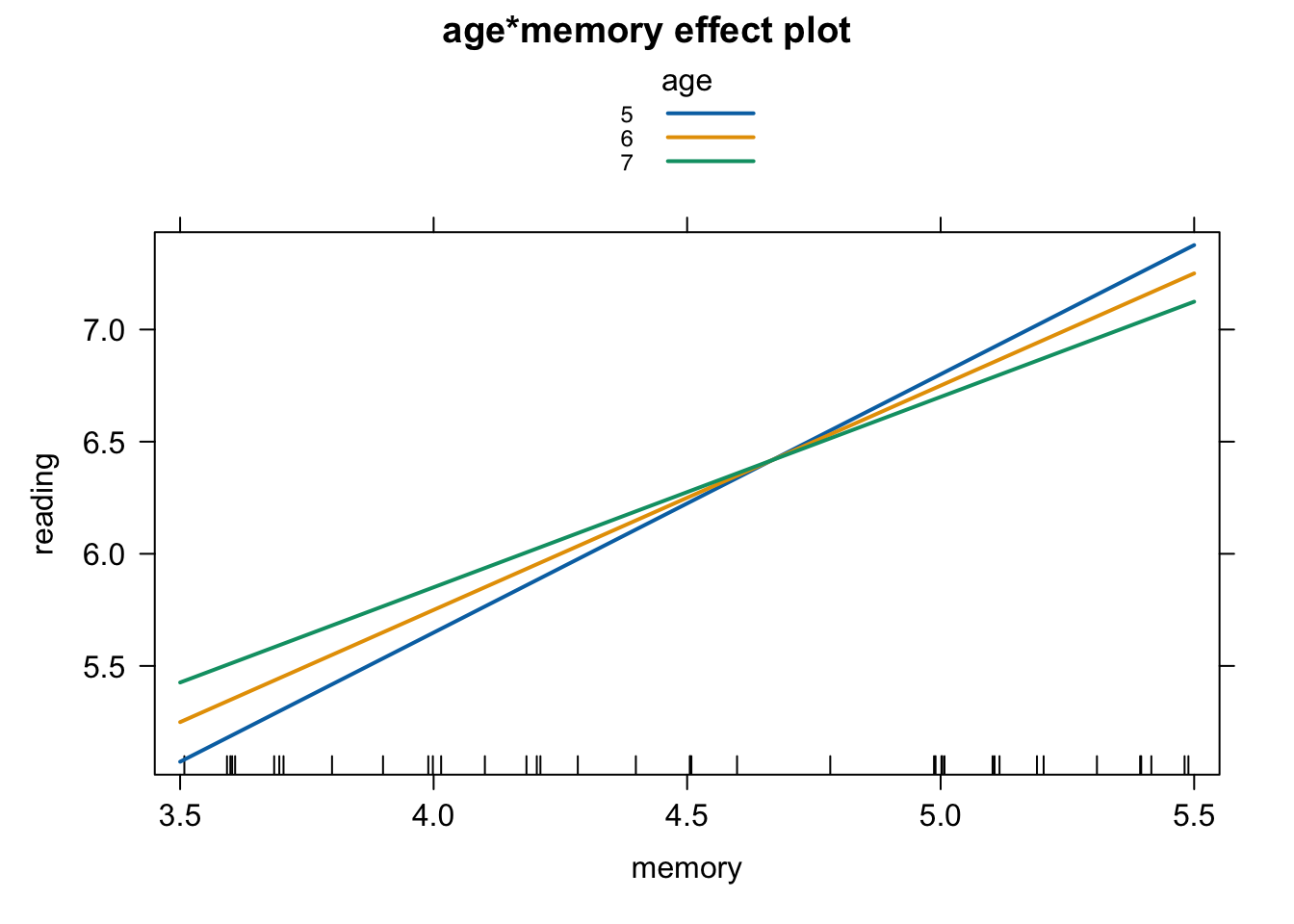
年齢が大きいほど記憶と読解力の関係は弱まる（直線の傾きが小さい）傾向があるようにも見えます。
ただし VIF の値が大きいので多重共線性の問題が生じていると考えられ、この分析結果は信用できるものではありません。
結局のところ、記憶（のみ）が読解力と関係するという結果であったと言えます。
因子分析
ユーモアスタイル質問紙に関するデータを用いて因子分析をして下さい。
データについて
Humor Styles Questionnaire (Martin et al., 2003) に対する 1071 名分の回答データです。
Martin, R. A., Puhlik-Doris, P., Larsen, G., Gray, J., & Weir, K. (2003). Individual differences in uses of humor and their relation to psychological well-being: Development of the Humor Styles Questionnaire. Journal of Research in Personality, 37, 48-75.
この質問紙はユーモアの様々な側面についての 32 個の質問からなる質問紙で、回答者は各質問に対して 1（全くそう思わない）から 5（とてもそう思う）の 5 段階で回答をしました。具体的な質問文を以下に掲載します。
Q1. I usually don’t laugh or joke around much with other people.
Q2. If I am feeling depressed, I can usually cheer myself up with humor.
Q3. If someone makes a mistake, I will often tease them about it.
Q4. I let people laugh at me or make fun at my expense more than I should.
Q5. I don’t have to work very hard at making other people laugh—I seem to be a naturally humorous person.
Q6. Even when I’m by myself, I’m often amused by the absurdities of life.
Q7. People are never offended or hurt by my sense of humor.
Q8. I will often get carried away in putting myself down if it makes my family or friends laugh.
Q9. I rarely make other people laugh by telling funny stories about myself.
Q10. If I am feeling upset or unhappy I usually try to think of something funny about the situation to make myself feel better.
Q11. When telling jokes or saying funny things, I am usually not very concerned about how other people are taking it.
Q12. I often try to make people like or accept me more by saying something funny about my own weaknesses, blunders, or faults.
Q13. I laugh and joke a lot with my closest friends.
Q14. My humorous outlook on life keeps me from getting overly upset or depressed about things.
Q15. I do not like it when people use humor as a way of criticizing or putting someone down.
Q16. I don’t often say funny things to put myself down.
Q17. I usually don’t like to tell jokes or amuse people.
Q18. If I’m by myself and I’m feeling unhappy, I make an effort to think of something funny to cheer myself up.
Q19. Sometimes I think of something that is so funny that I can’t stop myself from saying it, even if it is not appropriate for the situation.
Q20. I often go overboard in putting myself down when I am making jokes or trying to be funny.
Q21. I enjoy making people laugh.
Q22. If I am feeling sad or upset, I usually lose my sense of humor.
Q23. I never participate in laughing at others even if all my friends are doing it.
Q24. When I am with friends or family, I often seem to be the one that other people make fun of or joke about.
Q25. I don’t often joke around with my friends.
Q26. It is my experience that thinking about some amusing aspect of a situation is often a very effective way of coping with problems.
Q27. If I don’t like someone, I often use humor or teasing to put them down.
Q28. If I am having problems or feeling unhappy, I often cover it up by joking around, so that even my closest friends don’t know how I really feel.
Q29. I usually can’t think of witty things to say when I’m with other people.
Q30. I don’t need to be with other people to feel amused – I can usually find things to laugh about even when I’m by myself.
Q31. Even if something is really funny to me, I will not laugh or joke about it if someone will be offended.
Q32. Letting others laugh at me is my way of keeping my friends and family in good spirits.
dat = read.table( file = "https://htsuda.net/dataset/hsq.csv",
header = T, sep = "," )
head( dat, 1 )
## Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 Q12 Q13 Q14 Q15 Q16 Q17 Q18 Q19 Q20
## 1 2 2 3 1 4 5 4 3 4 3 3 1 5 4 4 4 2 3 3 1
## Q21 Q22 Q23 Q24 Q25 Q26 Q27 Q28 Q29 Q30 Q31 Q32 age gender
## 1 4 4 3 2 1 3 2 4 2 4 2 2 25 2
dim( dat )
## [1] 1071 34このデータで注意すべきこととして、各質問に対する回答は基本的に 1〜5 の値ですが、無回答の場合には -1 という値が入っています。無回答データを含んだままだと因子分析に悪影響があるので、それらを取り除く前処理を以下のようにして行います。
データの前処理
分析の前にデータを少し加工しておきます。
# 年齢と性別の列を捨てる
dat = dat[ , 1:32 ]
# 1つでも無回答のある人のデータを捨てる
dat[ dat == -1 ] = NA
dat = dat[ complete.cases( dat ), ]
# 残ったデータの数を確認
dim( dat )
## [1] 993 32無回答項目のある人を取り除くことで、データの数は 1071 から 993 へと少し減りました。
分析すること
KMO で因子分析の妥当性を確認する。
平行分析や MAP・BIC 基準で因子数を推測する。
因子分析を行い因子構造を確認する。
各因子に命名する。
解答例
平行分析および MAP・BIC 基準から、因子数を〜とした。因子分析の結果、各因子と質問項目に以下のような関係があった。〜。以上の結果から、各因子を〜と名付けた。
分析手続き
因子分析の妥当性を確認します。
KMO( dat )
## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = dat)
## Overall MSA = 0.88
## MSA for each item =
## Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 Q12 Q13 Q14 Q15
## 0.93 0.93 0.91 0.89 0.90 0.87 0.83 0.85 0.94 0.87 0.82 0.90 0.88 0.91 0.84
## Q16 Q17 Q18 Q19 Q20 Q21 Q22 Q23 Q24 Q25 Q26 Q27 Q28 Q29 Q30
## 0.89 0.90 0.84 0.90 0.85 0.90 0.88 0.83 0.83 0.87 0.90 0.85 0.94 0.87 0.81
## Q31 Q32
## 0.83 0.91全体指標が 0.88 なので OK。
では因子数を考えます。
# スクリープロットを描く
fa.parallel( dat, fa = "fa" )
abline( h = 0 )
# Parallel analysis suggests that the number of factors = 7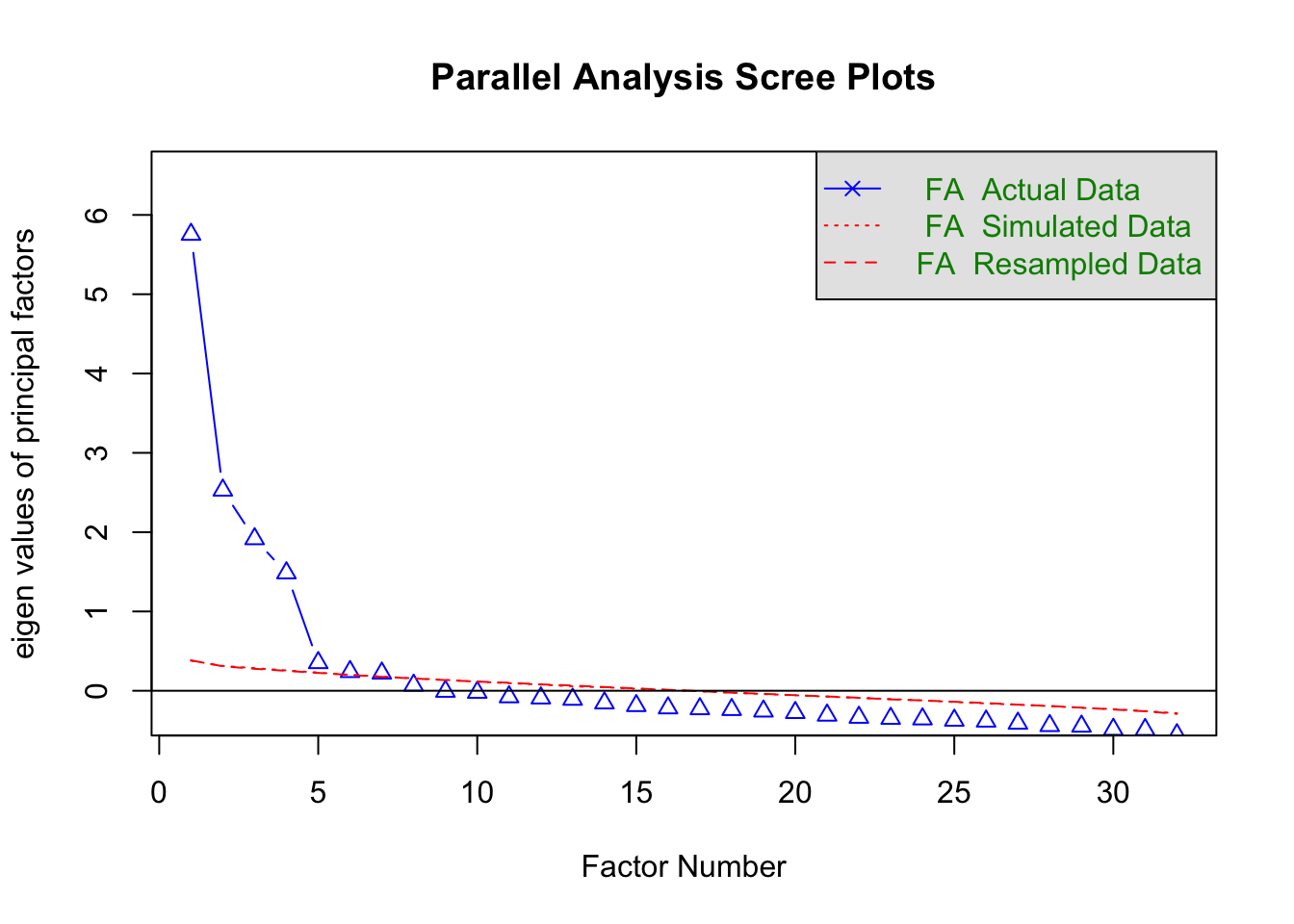
# MAP/BIC 基準の因子数の計算
VSS( dat, n = 8 )
# 略
# The Velicer MAP achieves a minimum of 0.01 with 4 factors
# BIC achieves a minimum of -1509.98 with 7 factors
# 略平行分析と BIC 基準は 7、MAP 基準は 4 となりました。
4〜7 の因子数のそれぞれの場合ごとの因子構造を確認してみます。
result = fa( dat, nfactors = 4, fm = "minres", rotate = "oblimin", use = "complete.obs" )
fa.diagram( result )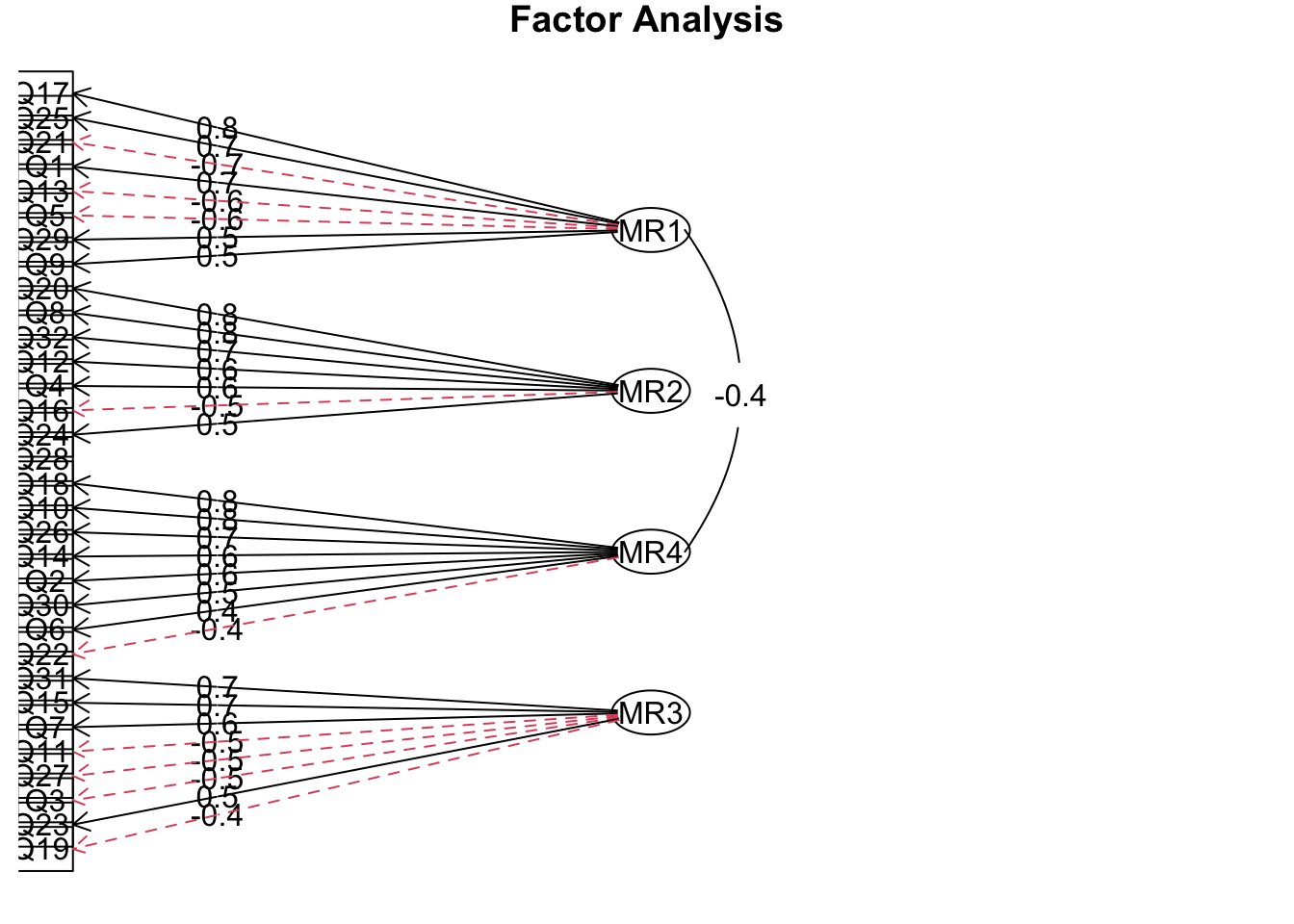
result = fa( dat, nfactors = 5, fm = "minres", rotate = "oblimin", use = "complete.obs" )
fa.diagram( result )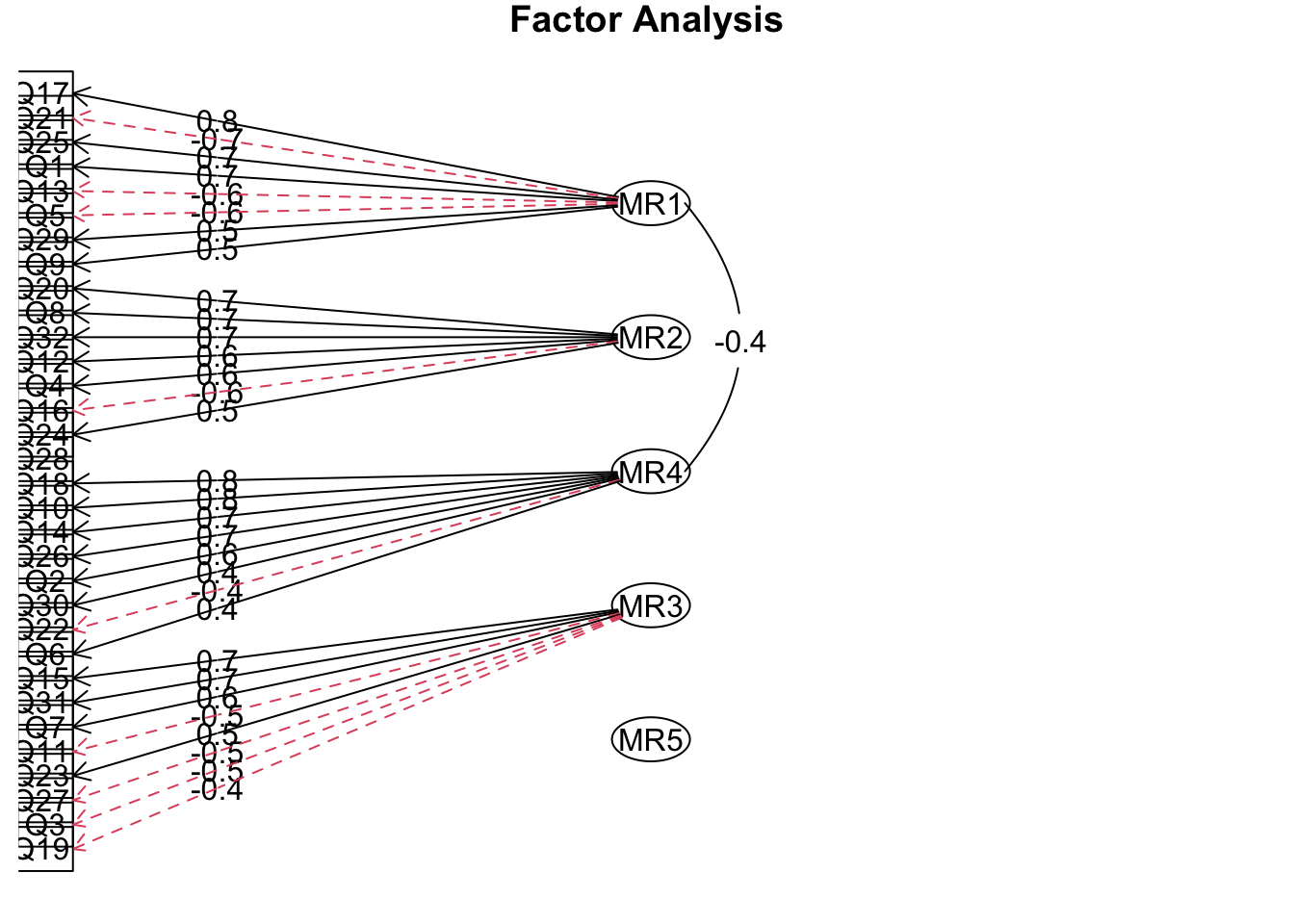
result = fa( dat, nfactors = 6, fm = "minres", rotate = "oblimin", use = "complete.obs" )
fa.diagram( result )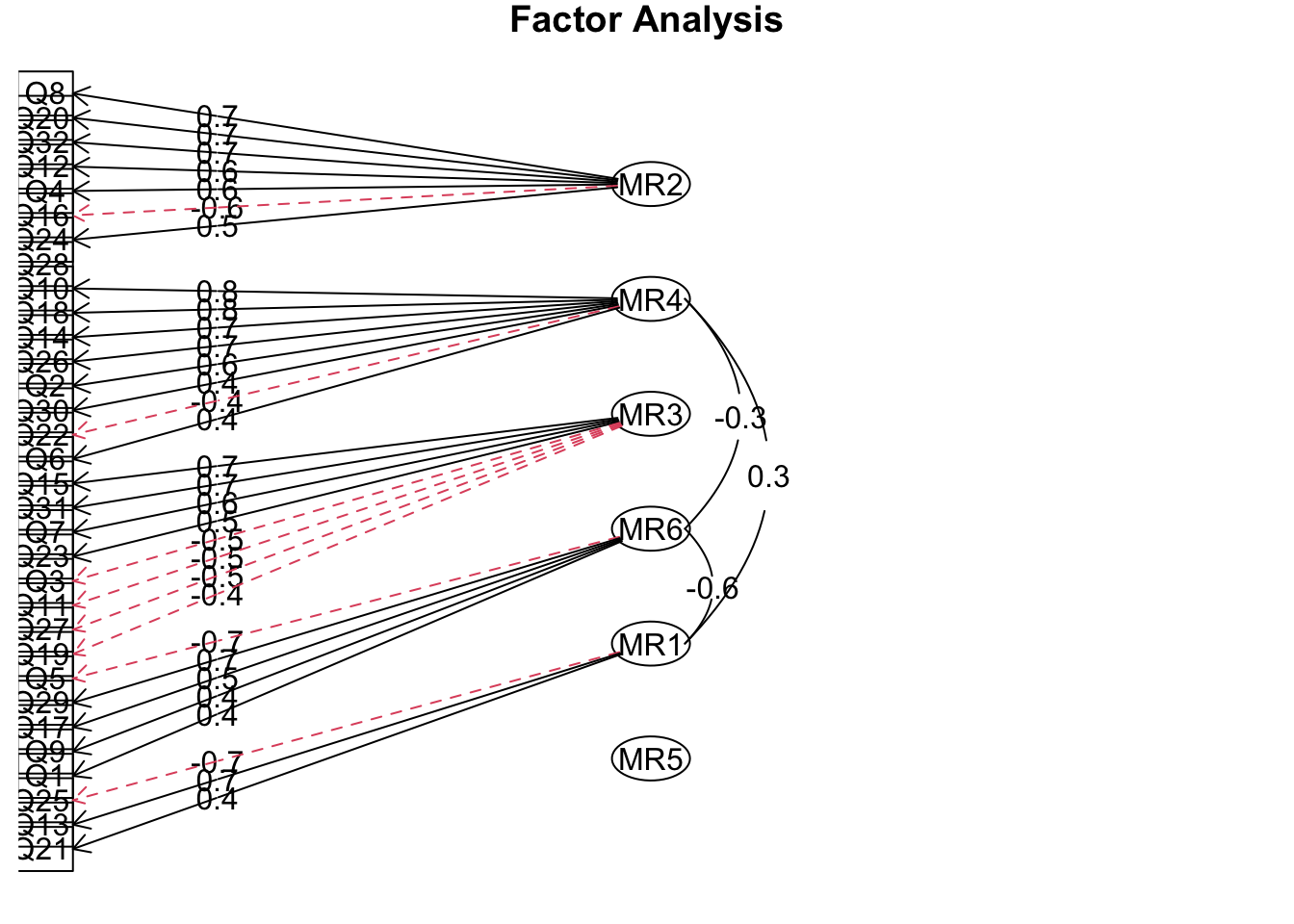
result = fa( dat, nfactors = 7, fm = "minres", rotate = "oblimin", use = "complete.obs" )
fa.diagram( result )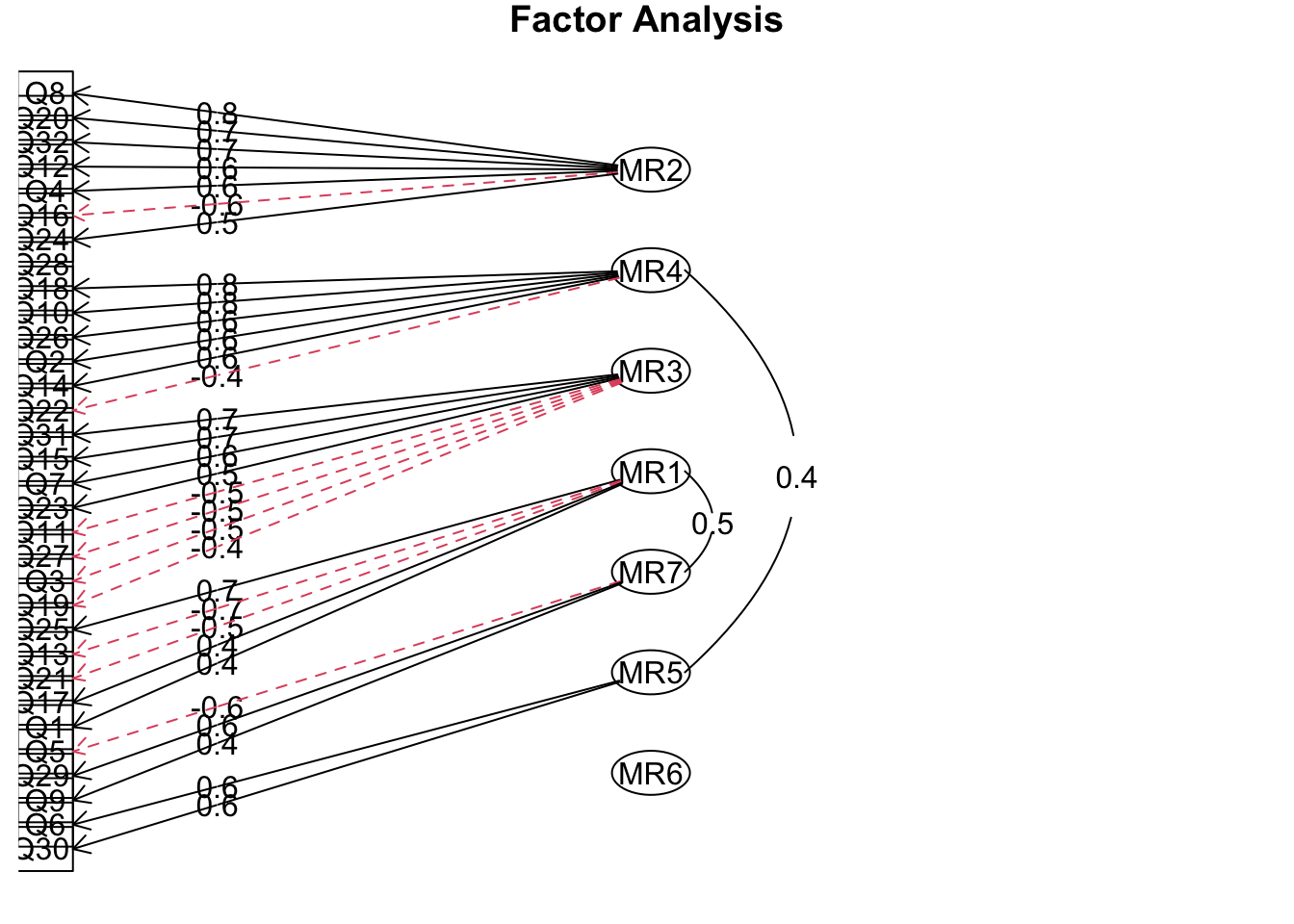
因子数は 4 で良さそうです。
因子構造を確認します。
result = fa( dat, nfactors = 4, fm = "minres", rotate = "oblimin" )
print( result$loadings, digits = 2, cutoff = 0.2 )
##
## Loadings:
## MR1 MR2 MR4 MR3
## Q1 0.66
## Q2 0.60
## Q3 -0.51
## Q4 0.64
## Q5 -0.60
## Q6 -0.24 0.40
## Q7 0.60
## Q8 0.75
## Q9 0.47
## Q10 0.76
## Q11 -0.55
## Q12 0.64
## Q13 -0.62
## Q14 0.65
## Q15 0.66
## Q16 -0.54
## Q17 0.76
## Q18 0.77
## Q19 -0.42
## Q20 0.75
## Q21 -0.68
## Q22 -0.36
## Q23 0.48
## Q24 0.50
## Q25 0.69
## Q26 0.66
## Q27 -0.53
## Q28 0.25
## Q29 0.55
## Q30 0.47
## Q31 0.69
## Q32 0.67
##
## MR1 MR2 MR4 MR3
## SS loadings 3.50 3.13 2.97 2.63
## Proportion Var 0.11 0.10 0.09 0.08
## Cumulative Var 0.11 0.21 0.30 0.38この結果から、
因子1: Q1, -Q5, Q9, -Q13, Q17, -Q21, Q25, Q29
因子2: Q4, Q8, Q12, -Q16, Q20, Q24, Q28, Q32
因子3: -Q3, Q7, -Q11, Q15, -Q19, Q23, -Q27, Q31
因子4: Q2, Q6, Q10, Q14, Q18, -Q22, Q26, Q30
という関連がわかりました（-記号は逆転項目）。
以上の結果から、
因子1: 親和的ユーモア
因子2: 自己防衛的ユーモア
因子3: 攻撃的ユーモア
因子4: 自己高揚的ユーモア
と名付けることにします。