9 基本的な統計分析
9.2 データセット
本ページで使うデータセットをまずは用意します。
本項では datarium パッケージのデータセットを利用することにします。
datarium パッケージはデータ分析の演習に適した様々なデータセットを提供しています。下記のページでデータセットの一覧とその概要を見ることができます。
https://rpkgs.datanovia.com/datarium/reference
datarium パッケージがインストールされていない場合はまずインストールしておきます。
パッケージの読み込みをします。
このパッケージが持つデータセットのうち jobsatisfaction と marketing の中身を確認してみます。
head( jobsatisfaction, 3 )
## id gender education_level score
## 1 1 male school 5.51
## 2 2 male school 5.65
## 3 3 male school 5.07
levels( jobsatisfaction$gender )
## [1] "male" "female"
levels( jobsatisfaction$education_level )
## [1] "school" "college" "university"
head( marketing, 3 )
## youtube facebook newspaper sales
## 1 276.12 45.36 83.04 26.52
## 2 53.40 47.16 54.12 12.48
## 3 20.64 55.08 83.16 11.16jobsatisfaction は仕事満足度(score)のデータで、説明変数として性別(male/female)と学歴(school/college,university)の2要因があります。
marketing はメディア(youtube/facebook/newspaper)への広告出稿料と売上げ額(sales)のデータです。
変数名が長いので、短い変数名で使えるようにしておきます。
9.3 各種統計量の計算
9.3.1 利用する関数
以下のような関数を使って様々な統計量を求めることができます。
x = job$score
# 要素数
length( x )
## [1] 58
# 総和
sum( x )
## [1] 403.87
# 平均値
mean( x )
## [1] 6.963276
# 中央値
median( x )
## [1] 6.38
# 分位数
quantile( x )
## 0% 25% 50% 75% 100%
## 4.780 5.800 6.380 8.515 10.000
# 最小値
min( x )
## [1] 4.78
# 最大値
max( x )
## [1] 10
# 範囲(最小・最大値)
range( x )
## [1] 4.78 10.00
# 不偏分散
var( x )
## [1] 2.357822
# 不偏標準偏差
sd( x )
## [1] 1.53552Rmisc パッケージの CI() 関数を使うと平均値の信頼区間を計算できます。
9.3.2 様々な統計料をまとめて計算する
summary()
summary() 関数を使うと、最小/最大値・平均値・分位数をまとめて計算できます。
# summary() 関数で基本統計量をまとめて計算できる
summary( job$score )
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 4.780 5.800 6.380 6.963 8.515 10.000
# 変数に保持して使う場合
stat = summary( job$score )
stat
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 4.780 5.800 6.380 6.963 8.515 10.000
# 第1分位点だけを表示させる
stat[ "1st Qu." ]
## 1st Qu.
## 5.8summary() 関数の引数にデータフレームを渡すと各列ごとの基本統計料が計算されます。
なお、要因型の列に対してはカウント数が計算されます。
(job データの gender を見ると男性28人・女性30人であることがわかります)
summary( job )
## id gender education_level score
## 1 : 1 male :28 school :19 Min. : 4.780
## 2 : 1 female:30 college :19 1st Qu.: 5.800
## 3 : 1 university:20 Median : 6.380
## 4 : 1 Mean : 6.963
## 5 : 1 3rd Qu.: 8.515
## 6 : 1 Max. :10.000
## (Other):52
summary( mkt )
## youtube facebook newspaper sales
## Min. : 0.84 Min. : 0.00 Min. : 0.36 Min. : 1.92
## 1st Qu.: 89.25 1st Qu.:11.97 1st Qu.: 15.30 1st Qu.:12.45
## Median :179.70 Median :27.48 Median : 30.90 Median :15.48
## Mean :176.45 Mean :27.92 Mean : 36.66 Mean :16.83
## 3rd Qu.:262.59 3rd Qu.:43.83 3rd Qu.: 54.12 3rd Qu.:20.88
## Max. :355.68 Max. :59.52 Max. :136.80 Max. :32.40pastecs::stat.desc()
pastecs パッケージの stat.desc() 関数を使うとさらに多くの統計量の計算が可能です。
library( pastecs )
stat.desc( mkt, basic = T, desc = T, norm = T, p = 0.95 )
## youtube facebook newspaper sales
## nbr.val 2.000000e+02 2.000000e+02 2.000000e+02 2.000000e+02
## nbr.null 0.000000e+00 1.000000e+00 0.000000e+00 0.000000e+00
## nbr.na 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## min 8.400000e-01 0.000000e+00 3.600000e-01 1.920000e+00
## max 3.556800e+02 5.952000e+01 1.368000e+02 3.240000e+01
## range 3.548400e+02 5.952000e+01 1.364400e+02 3.048000e+01
## sum 3.529020e+04 5.583360e+03 7.332960e+03 3.365400e+03
## median 1.797000e+02 2.748000e+01 3.090000e+01 1.548000e+01
## mean 1.764510e+02 2.791680e+01 3.666480e+01 1.682700e+01
## SE.mean 7.284974e+00 1.259794e+00 1.847977e+00 4.427159e-01
## CI.mean.0.95 1.436565e+01 2.484258e+00 3.644131e+00 8.730165e-01
## var 1.061417e+04 3.174159e+02 6.830040e+02 3.919947e+01
## std.dev 1.030251e+02 1.781617e+01 2.613435e+01 6.260948e+00
## coef.var 5.838736e-01 6.381882e-01 7.127912e-01 3.720775e-01
## skewness -6.880905e-02 9.276672e-02 8.813443e-01 4.014782e-01
## skew.2SE -2.001138e-01 2.697887e-01 2.563168e+00 1.167598e+00
## kurtosis -1.243594e+00 -1.276329e+00 5.675817e-01 -4.542196e-01
## kurt.2SE -1.817044e+00 -1.864874e+00 8.293070e-01 -6.636709e-01
## normtest.W 9.495094e-01 9.440052e-01 9.364005e-01 9.760262e-01
## normtest.p 1.692691e-06 5.197568e-07 1.127322e-07 1.682856e-03どのような統計量を計算するかを引数で変更することができます。
- basic : 欠損値の数や最小値最大値など
- desc : 平均値やその標準偏差(SE.mean)や95%信頼区間(CI.mean.0.95)など
- norm : 正規分布の統計量(歪度や尖度)と正規性の検定
- p: 信頼区間の計算に使う確率水準
グループごとの統計量を計算する
psych パッケージの describeBy() 関数を使うと、グループごとの統計量を計算できます。
library( psych )
# 性別ごとの score の統計量
describeBy( job$score, group = list( gender = job$gender ) )
##
## Descriptive statistics by group
## gender: male
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 28 7.06 1.76 6.34 7 1.34 4.78 10 5.22 0.46 -1.54 0.33
## ------------------------------------------------------------
## gender: female
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 30 6.87 1.31 6.45 6.76 1.07 4.93 9.57 4.64 0.64 -0.84 0.24
# 性別 x 学歴の score の統計量
describeBy( job$score,
group = list( education = job$education_level, gender = job$gender ) )
##
## Descriptive statistics by group
## education: school
## gender: male
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 9 5.43 0.36 5.51 5.43 0.43 4.78 5.94 1.16 -0.29 -1.2 0.12
## ------------------------------------------------------------
## education: college
## gender: male
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 9 6.22 0.34 6.3 6.22 0.31 5.58 6.74 1.16 -0.35 -0.89 0.11
## ------------------------------------------------------------
## education: university
## gender: male
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 10 9.29 0.44 9.2 9.28 0.43 8.7 10 1.3 0.45 -1.25 0.14
## ------------------------------------------------------------
## education: school
## gender: female
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 10 5.74 0.47 5.72 5.76 0.43 4.93 6.38 1.45 -0.12 -1.3 0.15
## ------------------------------------------------------------
## education: college
## gender: female
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 10 6.46 0.47 6.45 6.48 0.43 5.65 7.1 1.45 -0.13 -1.3 0.15
## ------------------------------------------------------------
## education: university
## gender: female
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 10 8.41 0.94 8.48 8.5 0.86 6.52 9.57 3.05 -0.58 -0.81 0.39.4 t 検定
t 検定では2つのグループ間の平均値に差があるかを調べます。
t.test 関数を使って t 検定が行えます。
関数の引数の与え方として以下の2通りがあります。
t.test( formula = , data = ): データフレームを使うt.test( x = , y = ): 各グループごとの数値ベクトルを使う
formula には ~ の左側に検定したい列名、右側にグループ分けに使う列名を書きます。
data にはデータフレームを入れます。
# 方法1
t.test( formula = score ~ gender, data = job )
##
## Welch Two Sample t-test
##
## data: score by gender
## t = 0.47084, df = 49.769, p-value = 0.6398
## alternative hypothesis: true difference in means between group male and group female is not equal to 0
## 95 percent confidence interval:
## -0.6311159 1.0175445
## sample estimates:
## mean in group male mean in group female
## 7.063214 6.870000
# 方法2
male = subset( job, gender == "male" )$score
female = subset( job, gender == "female" )$score
t.test( x = male, y = female )
##
## Welch Two Sample t-test
##
## data: male and female
## t = 0.47084, df = 49.769, p-value = 0.6398
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.6311159 1.0175445
## sample estimates:
## mean of x mean of y
## 7.063214 6.870000どちらの方法でも同じ結果になっているのが確認できます。
t = 0.47084 (p = 0.6398) で、性別によってスコアに有意な差があるとは言えません。
相関係数の検定と同様、alternative 引数を使って片側検知もできます。
また、対応のある t 検定をする場合には引数に paired = TRUE を加えます。
(デフォルトでは paired = FALSE、つまり対応のない t 検定をします)
9.5 相関
相関係数は量的変数同士の関係を記述するのに利用されます。相関係数は -1 から 1 までの範囲の値を取り、値の絶対値が大きいほど関係性の強さを示します。このセクションでは相関係数の計算方法と優位性検定について解説します。
9.5.1 marketing のデータ
datarium パッケージの marketing データの相関係数を計算します。
その前に、まずは散布図を描いてデータを視覚的に確認しましょう。
pairs() 関数を使うとペアごとの散布図をまとめて描くことができます。
第1引数で ~ 記号の右側に図に含めたい要素(列名)を + でつないで記述します。
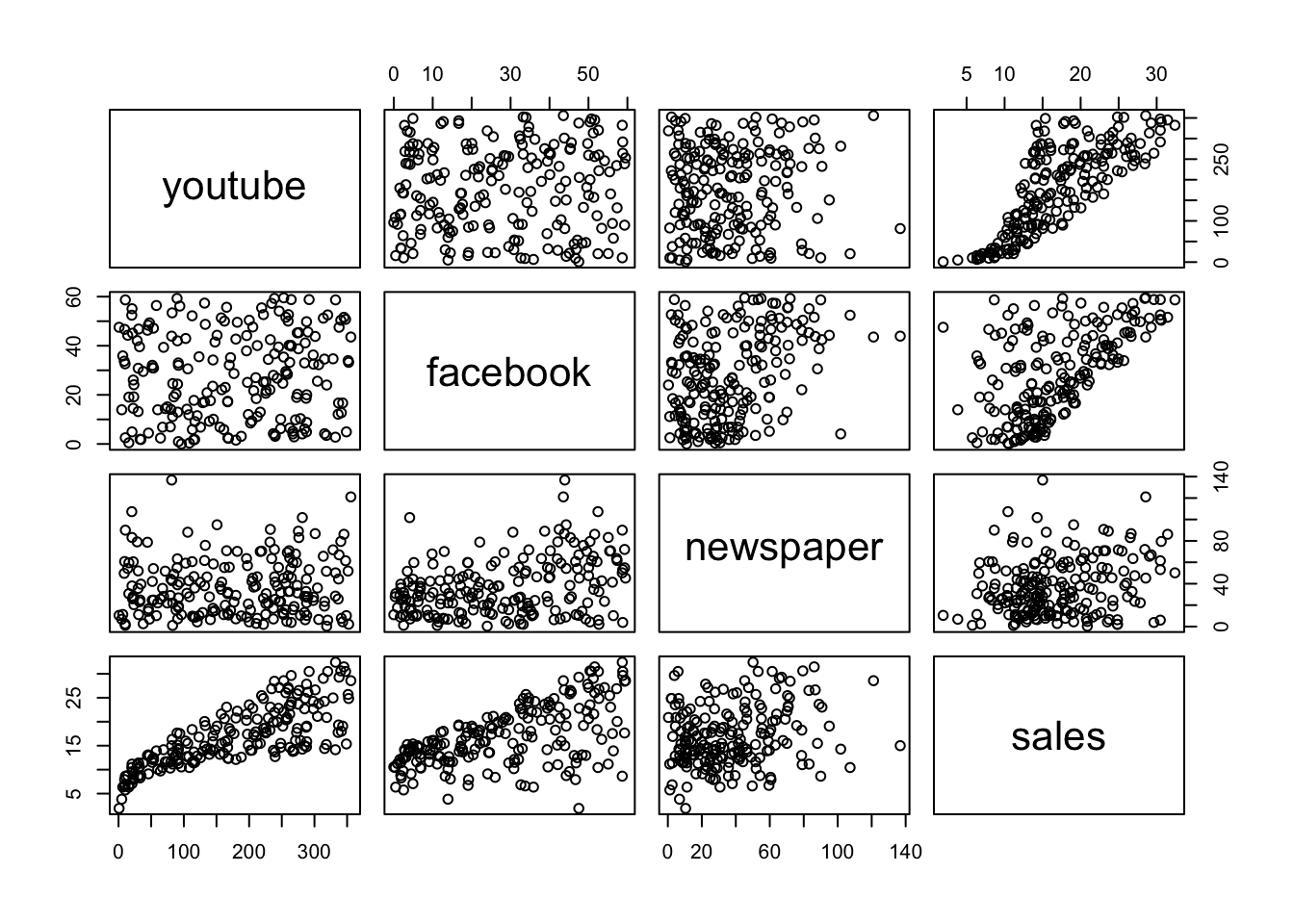
これを見ると youtube と sales、facebook と sales の間には正の相関がありそうです。
9.5.2 cor() 関数による相関係数の計算
cor() 関数を使うと相関係数の計算ができます。
# youtube と sales の相関係数
cor( x = mkt$youtube, y = mkt$sales )
## [1] 0.7822244
# facebook と sales の相関係数
cor( x = mkt$facebook, y = mkt$sales )
## [1] 0.5762226
# ペアごとの相関係数を全て計算
cor( mkt )
## youtube facebook newspaper sales
## youtube 1.00000000 0.05480866 0.05664787 0.7822244
## facebook 0.05480866 1.00000000 0.35410375 0.5762226
## newspaper 0.05664787 0.35410375 1.00000000 0.2282990
## sales 0.78222442 0.57622257 0.22829903 1.0000000上記の3つ目のように cor 関数にデータフレームごと入れれば全てのペアの相関係数が計算できて便利ですが、今回の分析ではSNS同士の相関には興味はないのでちょっと冗長です。
例えば以下のようにすれば、各 SNS への広告と sales 額の相関のみを計算できます。
# sales と 3種類のSNSとの相関係数のみを計算
cor( x = subset( mkt, select = sales ), y = subset( mkt, select = -sales ) )
## youtube facebook newspaper
## sales 0.7822244 0.5762226 0.2282999.5.3 相関係数の検定
cor.test() 関数で相関係数の検定が行えます。
cor.test( x = mkt$youtube, y = mkt$sales, method = "pearson" )
##
## Pearson's product-moment correlation
##
## data: mkt$youtube and mkt$sales
## t = 17.668, df = 198, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.7218201 0.8308014
## sample estimates:
## cor
## 0.7822244t 値は 17.668 で p 値は 2.2e-16 未満(p-value < 2.2e-16)と極めて小さく、有意な相関だと言えます。
cor.test() 関数は alternative という引数も持ち、デフォルトでは “two.sided” となっています(両側検定)。片側検定も可能で、正の相関を想定する場合は alternative = "greater"、負の相関を想定する場合は alternative = "less" とします。
2.2e-16 というのは 0.00000000000000022 のことですが、これは実際のところ .Machine$double.eps の値であり統計学的に意味のある値ではありません。この値について詳しくは help( .Machine ) を参照。
cor.test() 関数では一度にひとつの相関についてしか計算ができません。
psych パッケージの corr.test 関数を使うとペアごとの相関の検定が一度に行えます。
library( psych )
corr.test( mkt )
## Call:corr.test(x = mkt)
## Correlation matrix
## youtube facebook newspaper sales
## youtube 1.00 0.05 0.06 0.78
## facebook 0.05 1.00 0.35 0.58
## newspaper 0.06 0.35 1.00 0.23
## sales 0.78 0.58 0.23 1.00
## Sample Size
## [1] 200
## Probability values (Entries above the diagonal are adjusted for multiple tests.)
## youtube facebook newspaper sales
## youtube 0.00 0.85 0.85 0
## facebook 0.44 0.00 0.00 0
## newspaper 0.43 0.00 0.00 0
## sales 0.00 0.00 0.00 0
##
## To see confidence intervals of the correlations, print with the short=FALSE option相関係数と p 値が出力されます。
cor.test も corr.test も関数の返り値はリストであり、相関係数や p 値以外にも様々な計算結果が含まれています。
library( psych )
# リストの要素名を調べる
names( corr.test( mkt ) )
## [1] "r" "n" "t" "p" "p.adj" "se" "sef" "adjust"
## [9] "sym" "ci" "ci2" "ci.adj" "stars" "Call"
# リストの中の ci という名前の要素(信頼区間のデータ)を表示
corr.test( mkt )$ci
## lower r upper p
## youtb-facbk -0.08457548 0.05480866 0.1920890 4.408061e-01
## youtb-nwspp -0.08274345 0.05664787 0.1938652 4.256018e-01
## youtb-sales 0.72182010 0.78222442 0.8308014 1.467390e-42
## facbk-nwspp 0.22648989 0.35410375 0.4697658 2.688835e-07
## facbk-sales 0.47549537 0.57622257 0.6620366 4.354966e-19
## nwspp-sales 0.09248750 0.22829903 0.3557712 1.148196e-039.5.4 偏相関係数の計算
ある変数の影響を統制した上での相関関係を測るのが偏相関係数です。
ppcor パッケージの pcor() 関数を使うと偏相関係数の計算ができます。
library( ppcor )
pcor( mkt )
## $estimate
## youtube facebook newspaper sales
## youtube 1.00000000 -0.7670098 0.02725949 0.91976143
## facebook -0.76700982 1.0000000 0.20030129 0.84247816
## newspaper 0.02725949 0.2003013 1.00000000 -0.01262147
## sales 0.91976143 0.8424782 -0.01262147 1.00000000
##
## $p.value
## youtube facebook newspaper sales
## youtube 0.000000e+00 1.251529e-39 0.703042019 1.509960e-81
## facebook 1.251529e-39 0.000000e+00 0.004663912 1.505339e-54
## newspaper 7.030420e-01 4.663912e-03 0.000000000 8.599151e-01
## sales 1.509960e-81 1.505339e-54 0.859915050 0.000000e+00
##
## $statistic
## youtube facebook newspaper sales
## youtube 0.0000000 -16.735576 0.3817748 32.8086244
## facebook -16.7355760 0.000000 2.8622229 21.8934961
## newspaper 0.3817748 2.862223 0.0000000 -0.1767146
## sales 32.8086244 21.893496 -0.1767146 0.0000000
##
## $n
## [1] 200
##
## $gp
## [1] 2
##
## $method
## [1] "pearson"$estimate が相関係数、$p.value が p 値、$statistic が検定統計量、$n がサンプルサイズです。
9.5.5 相関関係の可視化
corrplot パッケージを使うと相関係数の値をヒートマップ表示できます。
library( corrplot )
# 相関係数
corrplot( cor( mkt ), method = "color", type = "full",
addCoef.col = "black", outline = F, diag = T,
col = colorRampPalette(c("deepskyblue1","white","indianred3"))(200),
tl.cex = 1.5, tl.pos = "lt", tl.col = "black",
number.cex = 1.5, cl.cex = 1 )
# 偏相関係数
corrplot( pcor( mkt )$estimate, method = "color", type = "full",
addCoef.col = "black", outline = F, diag = T,
col = colorRampPalette(c("deepskyblue1","white","indianred3"))(200),
tl.cex = 1.5, tl.pos = "lt", tl.col = "black",
number.cex = 1.5, cl.cex = 1 )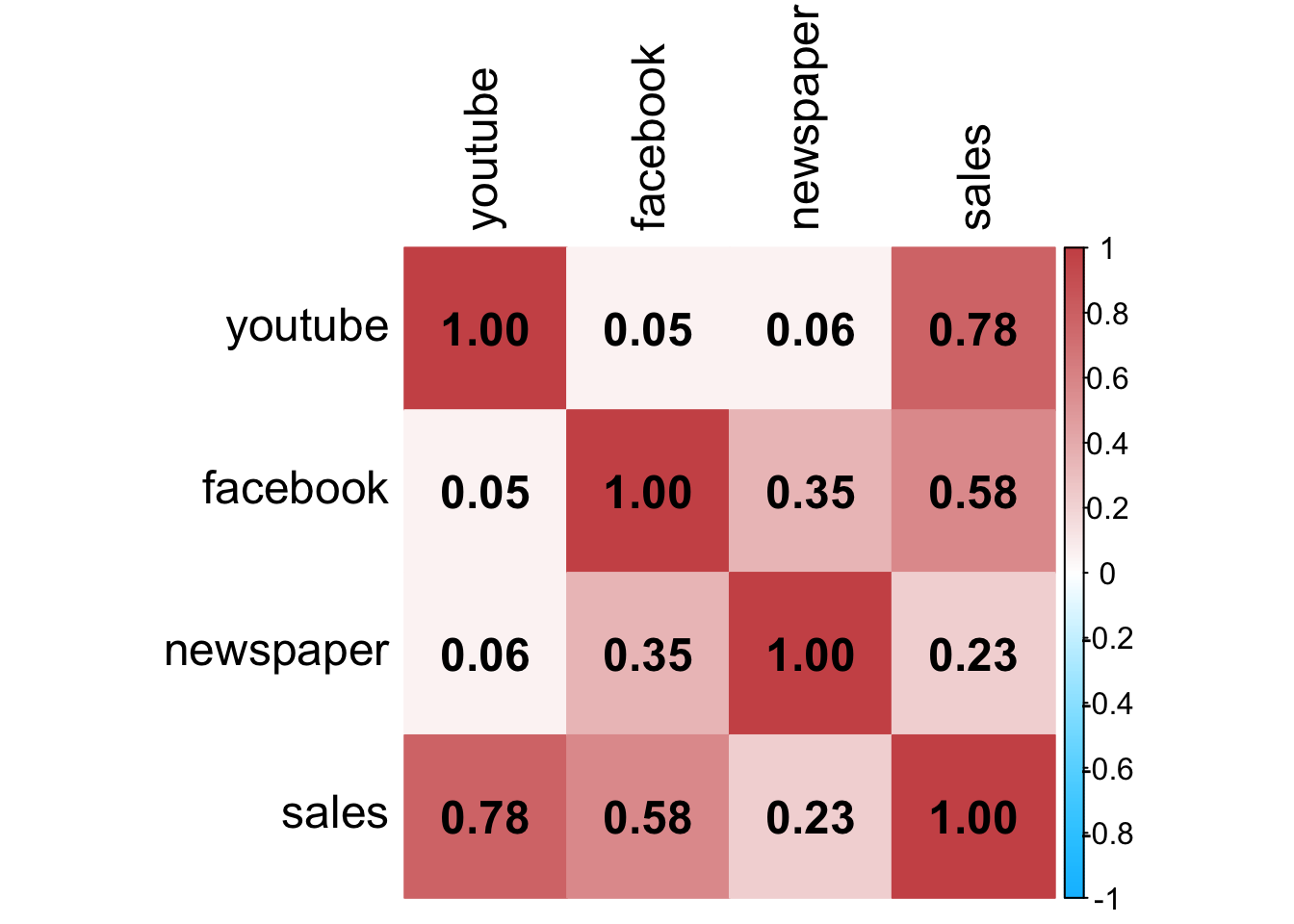
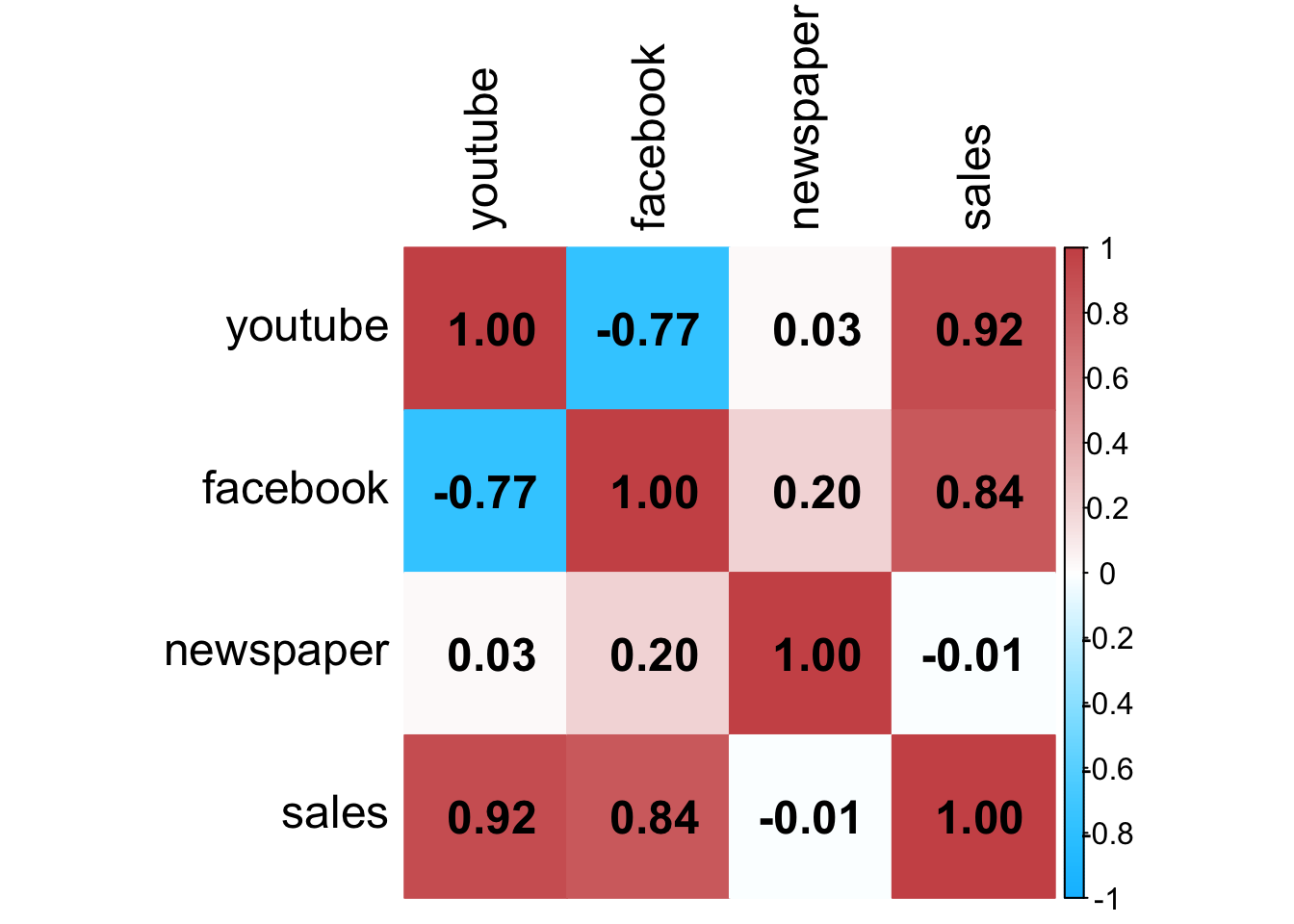
corrplot 関数の引数の意味については help( corrplot )を参照して下さい。