12 Rで分散分析

12.1 はじめに

2つのグループや条件の間で値に差があるかを調べる際はt検定を用います。他方で、3つ以上のグループや条件の間で値に差があるかを調べる際は分散分析を使います。

例として、Rに標準で含まれている chickwts（ひよこの体重データ）をみてみましょう。これは6種類の異なる餌をひよこに与えて育てた後の体重のデータであり、与える餌によって体重が異なるかどうかを調べるためのものです。

library(tidyverse)

dat = chickwts

# データの可視化（平均値と95%信頼区間）
fig = ggplot(dat, aes(x = feed, y = weight, fill = feed)) +
  stat_summary(fun.data = "mean_cl_normal", geom = "errorbar", width = 0.2) +
  stat_summary(fun = "mean", geom = "point", size = 3) +
  labs(x = "餌の種類（feed）", y = "体重（weight）") +
  theme_classic(base_size = 16) +
  theme(legend.position = "none")

plot(fig)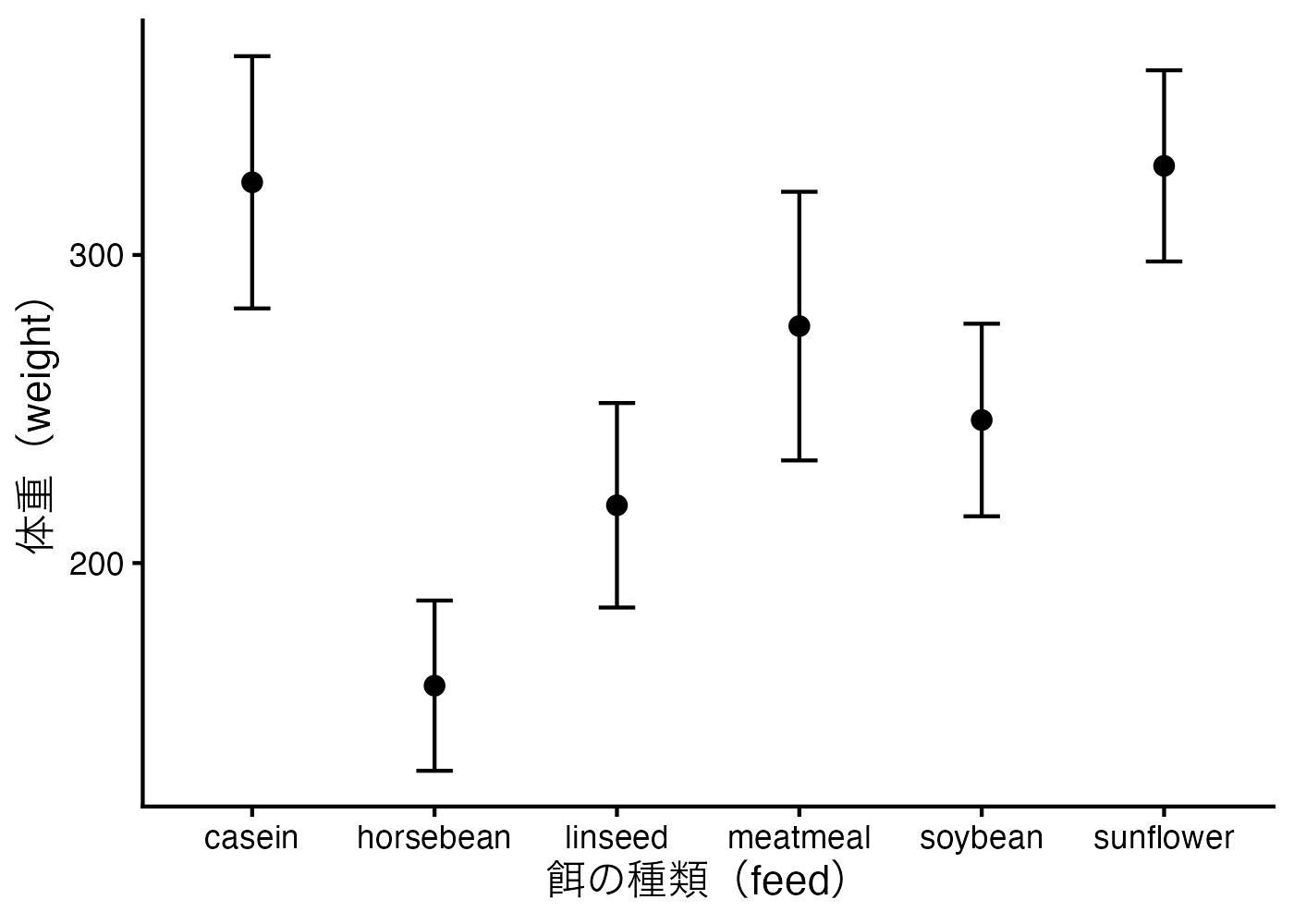

餌の種類によってひよこの体重には違いがあるように見えます。餌の種類は体重に対して統計的に有意な効果を持つのか、そして、どの餌とどの餌の間に差があるのかを、分散分析によって検討することができます。

12.1.1 パッケージのインストール

このページで使用するパッケージをあらかじめインストールしておいてください。

install.packages("qqplotr")    # Q-Qプロットの作成に使用する
install.packages("afex")       # パラメトリック分散分析などに使用する
install.packages("emmeans")    # 事後検定・推定周辺平均などに使用する
install.packages("effectsize") # 効果量の算出などに使用する
install.packages("rstatix")    # 非パラメトリック検定などに使用する
install.packages("ARTool")     # 多要因非パラメトリック検定などに使用する

12.2 なぜ分散分析が必要なのか

12.2.1 t検定を繰り返すことの問題点：多重性

たとえば、A、B、Cという3つのグループの平均値を比較したいとします。このとき、「AとB」「BとC」「AとC」というペアごとに、t検定を3回行えば良いと考えるかもしれません。しかし、このやり方には問題があります。

統計的仮説検定では、通常「0.05（5%）」を有意水準として設定します。これは「本当は差がないのに、差があると誤って判断してしまう確率（第一種の過誤／偽陽性）」を、あらかじめ5%以下に抑えるという約束事です。

問題は、検定を繰り返すほど、分析全体としての偽陽性を犯す確率が膨れ上がってしまうことです。これを「検定の多重性」の問題と呼びます。

1回のt検定で間違いを犯さない確率を 0.95 と定めます。
t検定を3回繰り返すと、そのすべてにおいて正しく判断できる確率は 0.95×0.95×0.95≈0.857（85.7%）まで低下します。
つまり、「複数実施された検定のうちの少なくとも1回は偽陽性（本当は差がないのに有意差ありと判定してしまうこと）が生じてしまう確率」は 1 - 0.95³ = 0.143（14.3%）まで増大します（本来はこの確率、つまり有意水準を5％にしたかったはずなのに）。

したがって、単純にt検定をグループ総当たりで繰り返すという方法では、「分析全体での偽陽性率」（ファミリーワイズ・エラー率と呼ばれます）が高まってしまうため、推奨されません。

［確認］ひよこのデータでは6つのグループがある。この場合、グループ総当たりでt検定を繰り返した場合のファミリーワイズ・エラー率はいくらになるか計算してください（答えは約53.7%です）

12.2.2 分散分析の役割：オムニバステストと検出力の向上

この多重性の問題を回避しつつ、より精度の高い判定を行うために考案されたのが分散分析（ANOVA：Analysis of Variance）です。

分散分析では、個別のペア比較を行う前に、全体のデータを用いて「すべてのグループの母平均が等しい」という仮説を検定します（これをオムニバステストといいます）。そして、オムニバステストが有意であった場合は具体的にどのペアに差があるかを探る「事後検定」に進みます。このような2段階の手続きを踏むことで、分析全体の偽陽性率の増大を防ぎます。

ただし、t検定を繰り返す場合でも、p値に「多重比較補正」を加えれば、偽陽性率の増大を抑えることは可能です。しかし、それでも分散分析が推奨される理由は、単なる多重性への対処以上に、「検出力（有意差を見つけ出す力）」に優れているという点にあります。

1. 誤差推定の安定

分散分析は全グループのデータを一括して解析するため、個別のt検定よりも多くのデータから「誤差（ばらつき）」を見積もることができます。
特に、各グループのサンプルサイズ（N数）がおよそ30未満と小さい場合には、他グループの情報を活用することで推定が安定し、検出力が高まります。

2. 多重比較における感度の維持

グループ数が多くなる（およそ5群以上）と、汎用的なp値の多重比較補正（Bonferroni法やHolm法など）では有意差を見逃してしまいやすくなります。
一方、分散分析とセットで使われる事後検定（Tukey法など）は、多群比較に特化して設計されているため、偽陽性を防ぎつつも高い検出力を維持できます。

分散分析は、「等分散性が仮定できる」「サンプルサイズが小さい」「グループ数が多い」といった条件下では、単にt検定を繰り返してp値を補正するよりも、差を見つけ出せる確率（検出力）が高まるため、効果的な分析方法となるのです。

12.2.3 補足：分散分析が最適とは言えないケース

他方で、以下のような状況では、分散分析ではなく、「ウェルチのt検定を繰り返し使用し、p値には多重比較補正を行う」という方法の方が、より信頼性の高い結果が得られます。

等分散性が崩れており、かつサンプルサイズが不揃いなとき
グループ間で分散が大きく異なり、かつ各群のサンプルサイズもバラバラな場合には、分散分析は用いず、ウェルチのt検定を個別に行い、p値をHolm法などで補正するやり方を採用する方が信頼性の高い選択肢となります（各ペアの分散を最も直接的に反映できるからです）。
特定のグループのばらつきが「ノイズ」として全体に波及するとき
分散分析は、全グループのばらつきを合体（プール）させて一つの「共通の誤差」を見積もります。そのため、特定の1グループだけに極端な外れ値があったり、その群だけ分散が著しく大きかったりする場合、そのノイズが「全てのペアの比較」における分母（誤差項）を大きくしてしまいます。その結果、本来は差があるはずの「安定した他のグループ同士の比較」までもが有意になりにくくなるという現象が起きます。個別のt検定であれば、このノイズの影響を当該グループを含むペアだけに限定でき、他のペアの検出力を守ることができます。
特定のペアの比較のみに関心があるとき
全ての組み合わせ（総当たり）を調べる必要がない場合、全体の平均からのズレを評価するオムニバステストは解析の目的からすると遠回りな手段になってしまう場合があります。関心のあるペアを事前に決めておき、それらのt検定のみを行う（p値の補正も行う）方が、検出力が維持でき、不要なノイズの影響も受けにくい解析となります。このようなやり方は計画比較（planned comparison）と呼ばれます。

12.3 用語の説明

12.3.1 オムニバス検定（omnibus test）

オムニバス検定は、分散分析を構成する効果項（主効果や交互作用）ごとに、主効果では「水準平均の差がゼロではない組が少なくとも1つ存在するか」を、交互作用では「一方の要因の水準間差が他方の要因の水準によって変化するものが少なくとも1つ存在するか」を検定します。

具体例：要因A（A1・A2の2水準）、要因B（B1・B2・B3の3水準）

主効果Aのオムニバス検定：B1・B2・B3の違いは平均してならし、A1とA2の平均が同じと言えるかを調べる。言い換えると、「A1とA2の平均差がゼロではないか（差があるか）」を検定する。
主効果Bのオムニバス検定：A1・A2の違いは平均してならし、B1・B2・B3の平均がすべて同じと言えるかを調べる。言い換えると、「B1・B2・B3のうち、平均差がゼロではない組が少なくとも1つあるか」をまとめて検定する（どの組が違うかはこの段階では特定しない）。
交互作用（A×B）のオムニバス検定：A1とA2の差（Aの効果）が、B1・B2・B3のどの水準で見ても同じように現れるかを調べる。もしBの水準によって、A1とA2の差が「大きくなったり小さくなったり」「符号が変わったり」するなら、Aの効果がBに依存していることになる。交互作用のオムニバス検定は、「B1・B2・B3のどこかで、A1とA2の差の出方が他のB水準と異なる（差の差がゼロではない）ものが少なくとも1つ存在するか」をまとめて検定する。

12.3.2 事後検定（post hoc test）

事後検定とは、オムニバス検定で主効果や交互作用に有意差が示された後に、「具体的にどの水準どうしが異なるのか」や「交互作用がある場合にどの水準で差の出方が変わるのか」を明らかにするために行う追加の比較です。

オムニバス検定は効果項ごとに「全体として差があるかどうか」を判定しますが、差が生じている場所（どの水準どうしの差か、どの条件で差の出方が変わるか）までは特定しません。そのため、オムニバス検定で有意差が示された場合には、ペア比較や単純比較などの事後検定によって差の場所を調べることが一般的です。事後検定は複数回の比較を伴うことが多いため、p値に多重比較補正を行います。

なお、研究開始前に仮説にもとづいて「比較したい組み合わせ（対比）」をあらかじめ決めておく方法があり、これを計画比較（planned comparison / planned contrast）と呼びます。計画比較では、知りたい対比が最初から明確なため、オムニバス検定を先に行わずに、最初からその対比を直接検定することもあります。

12.3.3 多重比較補正について

多重比較補正とは、同じデータに対して平均差などの検定を複数回行うと、偶然に「有意」と判定される確率（第1種過誤）が増えてしまう問題に対処するために、p値や有意水準、信頼区間などを調整して誤判定の増加を抑える手続きです。

分散分析の事後検定では以下の多重比較補正がよく使われます。

Bonferroni：最も保守的で検出力が低下しやすい。計算が簡単なので比較数が少ない場合には使いやすい。
Tukey：分散分析の事後検定として設計された方法。すべてのペアを比較する場合によく使われる。
Holm：一般的な場面で広く使える。Bonferroniより検出力が高い。
Sidak：Bonferroniに近いが、やや検出力が高い。

12.3.4 効果量について

分散分析のオムニバス検定においては以下の効果量がよく使われます。

偏η²（partial eta-squared）：ある要因が全体の変動の何％を説明しているかを表し、多要因計画で推奨される。心理学分野などでよく使われる。
一般化η²（generalized η²）：異なる実験デザイン間での比較に適しており、afex のデフォルト出力として採用されている。
ω²（omega-squared）：母集団の効果量の推定値。

球面性について

対応のある分散分析では、データが「球面性の仮定」（すべての水準間の差の分散が等しいという仮定）を満たす必要があります。球面性が満たされないとき、F検定のp値が不正確になります。球面性が満たされない場合は自由度を補正する方法が使われます。

この補正は球面性を満たすかどうかに関わらず常に適用しても問題ないため、3水準以上の対応あり要因では常に補正を行うことを推奨します。afexパッケージはデフォルトで代表的な球面性の補正法である Greenhouse-Geisser 補正を適用します。

12.4 分析手法の選択

分散分析にはいくつかの種類があり、データの分布や対応の有無に合わせて使い分ける必要があります。

1. データの正規性（パラメトリックか非パラメトリックか）

統計学には、データの分布（データの散らばり具合）に正規分布を仮定する「パラメトリック手法」と、それを仮定しない「非パラメトリック手法」があります。

パラメトリック手法
データが正規分布に従っていることを分析の前提とします。一般的に、一定の条件を満たしていれば検出力（差を見つけ出す力）が高いのが特徴です。
非パラメトリック手法
データの分布を問いません。たとえば、5件法のアンケート結果（リッカート尺度）のように、数値の間隔が厳密に等しいといえないデータ（順序尺度）や、サンプルサイズが極端に小さく分布が偏っている場合などには、非パラメトリック手法が適しています。

2. 要因の数

分析したい独立変数が1つ（1要因）か、2つ以上（多要因）かという基準です。

冒頭のひよこの例では「餌の種類」という要因しかないので、1要因の分散分析に該当します（より詳しく言えば、1要因6水準の分散分析です）。
パラメトリック手法の場合は1要因でも2要因以上でも同じやり方で分散分析が行えますが、非パラメトリック手法の場合は1要因の場合（フリードマン検定やクラスカル・ウォリス検定）と多要因の場合（ART）で異なる分析方法を用いる必要があります。

3. 測定のデザイン（対応ありか対応なしか）

次に、データがどのような構造（デザイン）で測定されたのかを考慮します。

対応なし（独立したデータ / Between-subjects）
「餌Aを食べたヒヨコ群と餌Bを食べたヒヨコ群」や「学生が3群に分かれてそれぞれの別の科目の試験を受けた」というケースのように、各グループが別の個体から構成されている場合です。
複数の要因がある場合は、すべての要因が対応なしの場合です。
対応あり（反復測定データ / Within-subjects / Repeated measures）
「同じヒヨコが、生後10日目、20日目、30日目に測定された」というケースや、「すべての学生がA、B、Cという3つの科目の試験を受けた」というケースなどのように、同じ個体から何度もデータを取っている場合です。
複数の要因がある場合は、すべての要因が対応ありの場合です。
混合計画（mixed-design）
2つ以上の要因があり、対応なしの要因と対応ありの要因が両方存在する場合です。

12.4.1 分散分析の分類表

各分類ごとで使用する分散分析の名称を以下の表に整理しました。

正規性	要因数	対応の有無	検定名
パラメトリック	1	なし	一元配置分散分析
パラメトリック	1	あり	一元配置反復測定分散分析
パラメトリック	2以上	すべてなし	多元配置分散分析
パラメトリック	2以上	すべてあり	多元配置反復測定分散分析
パラメトリック	2以上	混合	多元配置混合計画分散分析
非パラメトリック	1	なし	クラスカル・ウォリス検定
非パラメトリック	1	あり	フリードマン検定
非パラメトリック	2以上	任意	整列ランク変換分散分析（ART）

12.4.2 パラメトリック手法を使って良いかの判断基準

パラメトリック手法を選んで良いかを判断するためにデータの正規性を確認する際は、以下の観点から総合的に検討します。

1. サンプルサイズ（データの件数）による判断

統計学には「中心極限定理」という理論があります。これは、各グループのサンプルサイズが十分に大きい（一般に30以上が目安）場合、元のデータが多少歪んでいても、平均値の計算結果は正規分布に従うという性質です。
そのため、サンプルサイズが大きい場合は、Q-Qプロットが多少直線から外れていても、パラメトリック手法を適用しても大きな問題はないとされます。
反対に、サンプルサイズが小さい場合（各群10未満など）は、Q-Qプロットによる判断が当てにならないため、非パラメトリック手法を用います。

2. 視覚的な確認（Q-Qプロット）

中規模のサンプルサイズ（群ごとに10から30程度）の場合、Q-Qプロットによる確認を行います。
Q-Qプロット（Quantile-Quantile Plot）とは、実際のデータと正規分布を比較するグラフです。
Q-Qプロットにおいてデータ点が直線状に並んでいれば正規分布に近いと判断できます。ヒストグラムでは分かりにくい分布の端のわずかな歪みまで確認できるのがメリットです。

3. 正規性の検定手法の扱い

正規性からの逸脱を判定する検定としてShapiro-Wilk検定などが有名ですが、以下のような問題があるため注意が必要です。
- サンプルサイズが小さいと、大きな歪みがあっても有意ではないと判定されやすく、正規性からの逸脱を見逃してしまいやすい。
- サンプルサイズが大きいと、実用上問題ないわずかな歪みしかないのに、有意である（正規分布ではない）と判定されやすく、不必要に厳しい判定をしてしまう。

したがって、パラメトリック手法を選んで良いかを判断する際は、

サンプルサイズが大きい場合（各群30以上など）は、パラメトリック手法を選んでよい（ただし、異常値や外れ値がないかはチェックしておく）。
小サンプルの場合（各群10未満など）は非パラメトリック手法を使う。
中規模のサンプルの場合（各群10から30程度）は、Q-Qプロットによる正規性のチェックを行う。

という基準を用いるとよいでしょう。

Q-Qプロットを用いた正規性の判断

qqplotr パッケージを用いると、Q-Qプロットの作成が容易に行えます。

主に以下の3つの関数を使います：

stat_qq_band()：信頼帯（Confidence Band）と呼ばれる範囲を描画します。
stat_qq_line()：理想的な正規分布を示す基準線を描画します。
stat_qq_point()：実際のデータ値をプロットします。

library(tidyverse)
library(qqplotr)

# データの準備
dat = chickwts

# Q-Qプロットの作成
fig = ggplot(dat, aes(sample = weight)) +
  qqplotr::stat_qq_band(fill = "gray80", alpha = 0.5) +
  qqplotr::stat_qq_line(color = "steelblue", linewidth = 1.2) +
  qqplotr::stat_qq_point(size = 1) +
  facet_wrap(~ feed) +
  theme_bw(base_size = 14)

plot(fig)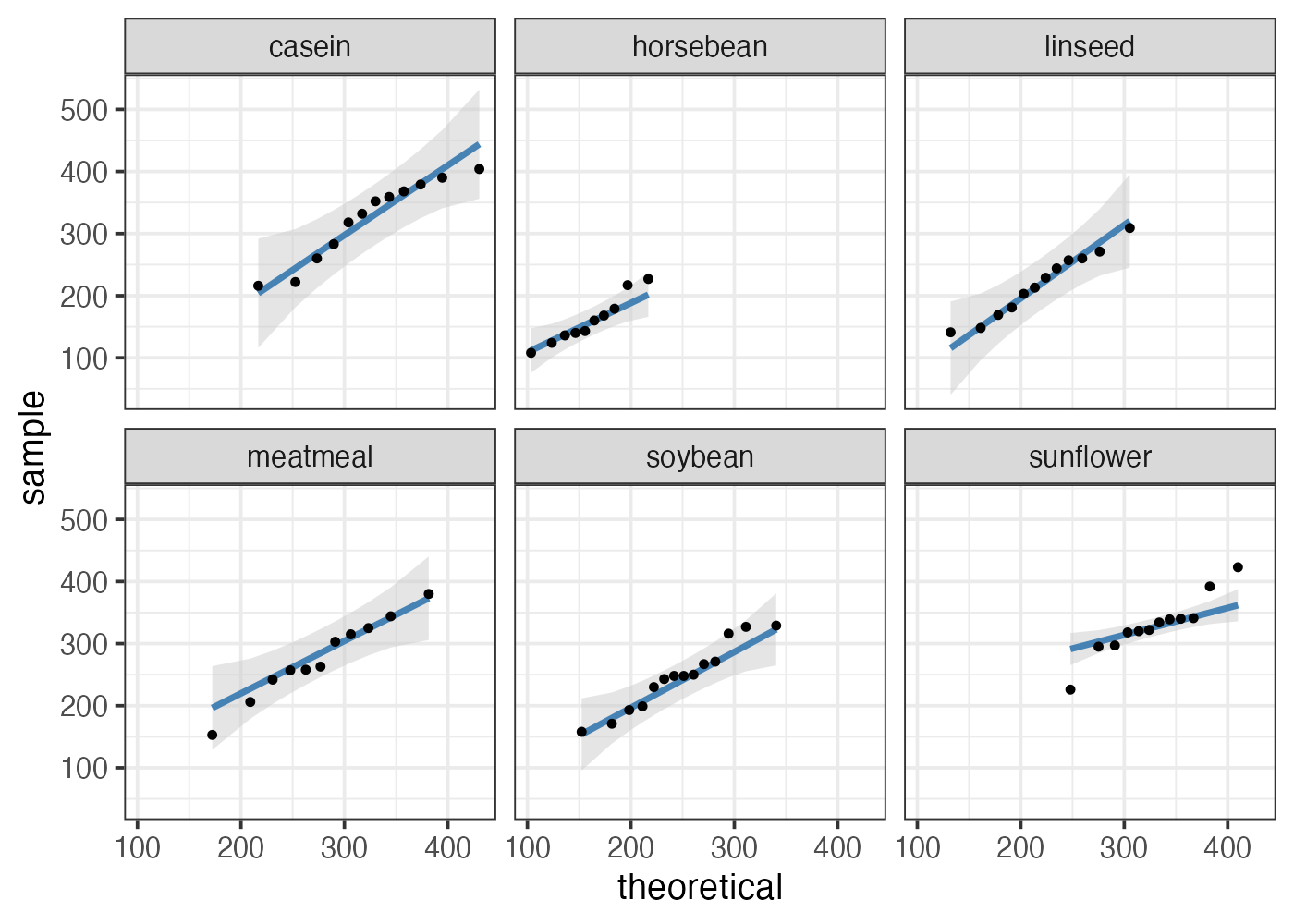

Q-Qプロットによる正規性の判断は以下のような基準で行います。

信頼帯（上の図の灰色の帯）にほぼ全てのデータの点が収まっていれば、正規分布であるとみなし、パラメトリック手法を使って良いと判断します。
データの両端にある1, 2点ほどが信頼帯から少しはみ出す程度であれば、実用上の影響は小さいと考え、パラメトリック手法を用いることが一般的です。
反対に、多くの点が信頼帯から外れている場合は正規分布から逸脱している可能性が高いため、非パラメトリック手法を選びます。
点の列が全体的にU字・逆U字・S字などの形状をしている場合は要注意です。それは、データが正規分布とは異なる構造を持っていることの兆候です。ただし、その場合でもほとんどの点が信頼帯の範囲に収まっているのであれば、パラメトリック手法を使って構いません。

上の図の場合、caseinグループは全体的に逆U字（山形）の曲線になっていて少し怪しいものの、全ての点が信頼帯に収まっているので、正規性があるとみなしてよいと考えられます。

sunflowerは両端の点の逸脱が大きいように見えますが、これは青線や信頼帯を引く際の設定に由来する、見かけ上の逸脱だと考えられます。この両端の点を結ぶようにして図にペンを重ねれば、全ての点はペンの下に隠れます。つまり、点は直線的に並んでいるとみなせます。

stat_qq_line（図の青線）は、デフォルトでは第1四分位数と第3四分位数の2点を結ぶというやり方で直線を作成します。そのため、両端付近の値は無視されます。
今回のsunflowerの場合、この設定を変更し、より広い範囲（10%点と90%点）を使って直線を引くようにする方がより適切かもしれません。
stat_qq_band()関数とstat_qq_line()関数の両方にqprobs = c(0.1, 0.9)という引数を追加してみてください。sunflowerのデータ点も信頼帯に収まっているのが確認できます。

以上から、このひよこの体重データはすべてのグループで正規性が満たされていると判断できます。

［確認］ひよこの体重データを分散分析する場合、分散分析の分類表の中のどの分析法を選べばよいでしょうか？

12.5 データの準備と事前チェック

分散分析を正しく行うためには、データの形式を整える前処理が重要です。Rの分析パッケージ、たとえば afex パッケージは、特定のデータ形式を前提としています。

このセクションでは以下のチェック項目を説明します。

データに必要な列はあるか
Long形式への変換
要因列をfactor化し、水準の並び順を指定する
重複データの削除
繰り返し測定の集約処理
欠損値の扱い
記述統計の確認
外れ値の確認

まずは、このセクションで使用するサンプルデータを作成します。

library(tidyverse)

# 1. サンプルデータの作成（ワイド形式・重複あり・欠損あり）
raw = data.frame(
  id = c("s01", sprintf("s%02d", 1:10)),
  group = c("A", "A", "A", "A", "A", "B", "B", "B", "B", "B", "B"),
  morning = c(50, 50, 48, 52, 55, 60, 62, 58, 65, 61, 63),
  noon = c(55, 55, 53, 58, 60, 65, 68, 63, 70, 66, 68),
  night = c(60, 60, 58, 62, 65, NA, 75, 70, 80, 72, 177)
)

10人分の参加者を2つのグループ（A、B）に分け、3つの時間帯（朝、昼、晩）でテストを受けた時の成績を想定したデータです。

12.5.1 データ構造の確認

分散分析では、「誰が（ID列）」「どの条件で（要因列）」「いくらだったか（値の列）」という情報が必要です。

参加者IDの列（列名の例：id, subject など）
要因を示す列（列名の例：group, cond, time など）
従属変数の列（列名の例：dv, value, socre など）

今回のサンプルデータは「グループ」と「時間帯」の2つの要因を持ちます。グループは group という名前の列になっていますが、時間帯の方は3つの列（morning, noon, night）に別れて値が格納されている状態（ワイド形式）です。

12.5.2 ロング形式への変換

データがワイド形式の場合はロング形式に変換します。

Long形式：id・要因列・従属変数が縦に並ぶ
Wide形式：ある参加者のデータが横に並んでいる。

ロング形式への変換には pivot_longer() 関数を使います。引数の意味は以下のとおりです：

cols：Long形式に変換したい列を指定
names_to：元の列名を格納する新しい列の名前
values_to：値を格納する新しい列の名前

# pivot_longer を使用して、morning, noon, nightをロング化する
dat = tidyr::pivot_longer(
  raw,
  cols = c(morning, noon, night),
  names_to = "time",
  values_to = "score"
)

ワイド形式の場合は分析対象となる測定値（従属変数）が複数の列（morning, noon, night）に分かれていましたが、ロング形式では score という1つの列のみに従属変数の値が集約されています。このように、ロング形式では1つの測定値が1行に対応するようにデータが表現されます。

12.5.3 要因列をfactor化し、水準の並び順を指定する

要因（独立変数）は、factor型に変換しておくことが重要です。factor化することで、分析時に正しくグループとして認識されます。

また、水準（level）の順序を明示的に指定することで、分析結果やグラフの表示順序を指定できます。今回の時間帯データでは「朝 → 昼 → 晩」という順序にしておくのが自然でしょう。

# 因子型への変換と水準の指定
dat$group = factor(dat$group, levels = c("A", "B"))
dat$time = factor(dat$time, levels = c("morning", "noon", "night"))

# 水準の順序が正しく設定されたか確認
levels(dat$group)
## [1] "A" "B"
levels(dat$time)
## [1] "morning" "noon"    "night"

水準の順序は検定結果の解釈にも影響します。もしグループ要因が統制条件と実験条件といった水準から構成される場合は、統制条件を基準（最初の水準）にしておくと結果の解釈がしやすくなります。

12.5.4 重複データの削除

入力ミスなどによって、同一のデータが複数回入力されている場合は、それを除去するなどの対処が必要です。特定の列の行数をカウントするとこのようなデータの重複に気づきやすいです。

# 各参加者の行数を確認（ミスが無ければすべて同じ値のはず）
table(dat$id)
## 
## s01 s02 s03 s04 s05 s06 s07 s08 s09 s10 
##   6   3   3   3   3   3   3   3   3   3

s01の参加者のデータがダブっていることがわかります。

# 重複行の除去：まったく同じ内容の行を取り除きます
dat = dplyr::distinct(dat)

これで同一のデータを取り除くことができました。

（重複データの確認はワイド形式のデータの時点で行う方がわかりやすいかもしれません。）

12.5.5 繰り返し測定の集約処理

今回のサンプルデータでは該当しませんが、もし各参加者が条件ごとに複数回の測定を受けていたような場合は、それらを事前に集約する必要があります。

たとえば、もし各参加者が時間帯ごとに3回ずつの試行を行っていた場合は、それらの値を平均するなどして集約します。

# 繰り返し測定があるデータの例（参考）
# 参加者×条件（グループと時間帯と試行）ごとに平均値で集約する場合
# dat = dat %>%
#   dplyr::group_by(id, group, time, trial) %>%
#   dplyr::summarise(score = mean(score, na.rm = TRUE), .groups = "drop")

集約に使う代表値としては、以下のような選択肢があります：

平均値（mean）：最も一般的だが、外れ値の影響を受けやすい
中央値（median）：外れ値に対して頑健

どちらを使うかはデータの性質や研究の目的に応じて判断してください。

12.5.6 欠損値の扱いについて

データ（繰り返し測定のあるデータの場合は集約処理済みのデータ）に NA（欠損値）が含まれている場合、主に2つの考え方があります。

リストワイズ削除（Complete-case analysis）： 1か所でも欠損がある参加者のデータを、すべての分析から完全に除外します。
ペアワイズ削除（Pairwise deletion）：その時々の分析に必要な変数が揃っていれば、欠損がない範囲でデータを利用します。

対応のある分散分析では、ある条件で欠損がある参加者はその参加者のデータを丸ごと除外することになります。

欠損の割合が高い場合（目安として5〜10%以上）、その欠損がランダムに生じているか（MCAR: Missing Completely At Random）を確認してください。特定のグループや条件で欠損が発生しやすいなど、欠損の仕方が偏っている場合、結果に偏りが出る可能性があるため注意が必要です。

12.5.7 記述統計の確認

簡単な集計作業を行ってデータの様子を見ておくと良いでしょう。

aggregate(score ~ time + group, data = dat, FUN = mean)
##      time group    score
## 1 morning     A 51.25000
## 2    noon     A 56.50000
## 3   night     A 61.25000
## 4 morning     B 61.50000
## 5    noon     B 66.66667
## 6   night     B 94.80000

データの集計については以下のページで詳しく説明しています。
https://htsuda.net/stats/overview.html

12.5.8 外れ値の確認

外れ値がないかを確認します。さまざまな外れ値の基準がありますが、手っ取り早くやるなら箱ひげ図を描くとよいでしょう。

箱ひげ図では、IQRルールに基づいて外れ値が検出されます。IQR（四分位範囲）は第3四分位数（Q3）から第1四分位数（Q1）を引いた値で、箱の高さに相当します。箱ひげ図では、Q1 − 1.5×IQR より小さい値、または Q3 + 1.5×IQR より大きい値が、外れ値として点で表示されます。

fig = ggplot(dat, aes(x = time, y = score, fill = group)) +
  geom_boxplot() +
  theme_classic()

plot(fig)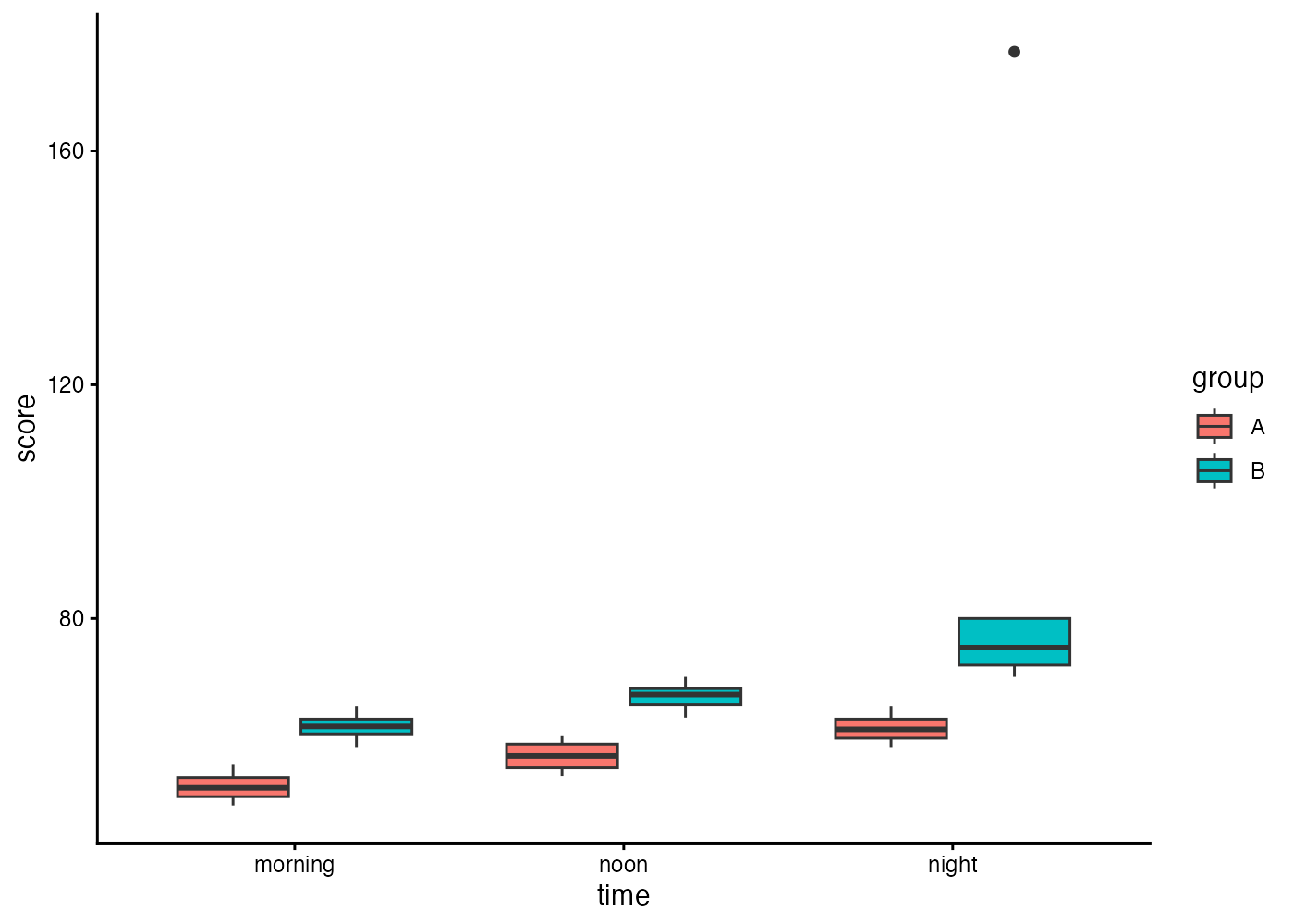

Group Bの night 条件で点が表示されており、これが外れ値です。

もしその外れ値が入力ミスやあり得ない値の場合は、それを欠損値（NA）に置き換えるとよいでしょう。

その外れ値があり得る範囲の値であるなら、もしそれを除外する場合は正当な理由が必要となります。

12.6 パラメトリック分散分析

12.6.1 1要因分散分析（対応なし）

独立した複数のグループ間で平均値を比較する際に使用します。

# データ
dat = chickwts
dat$id = factor(1:nrow(dat))

# 可視化
fig = ggplot(dat, aes(x = feed, y = weight, fill = feed)) +
    geom_boxplot(width = 0.3) +
    theme_classic(base_size = 16) +
    theme(legend.position = "NA")
plot(fig)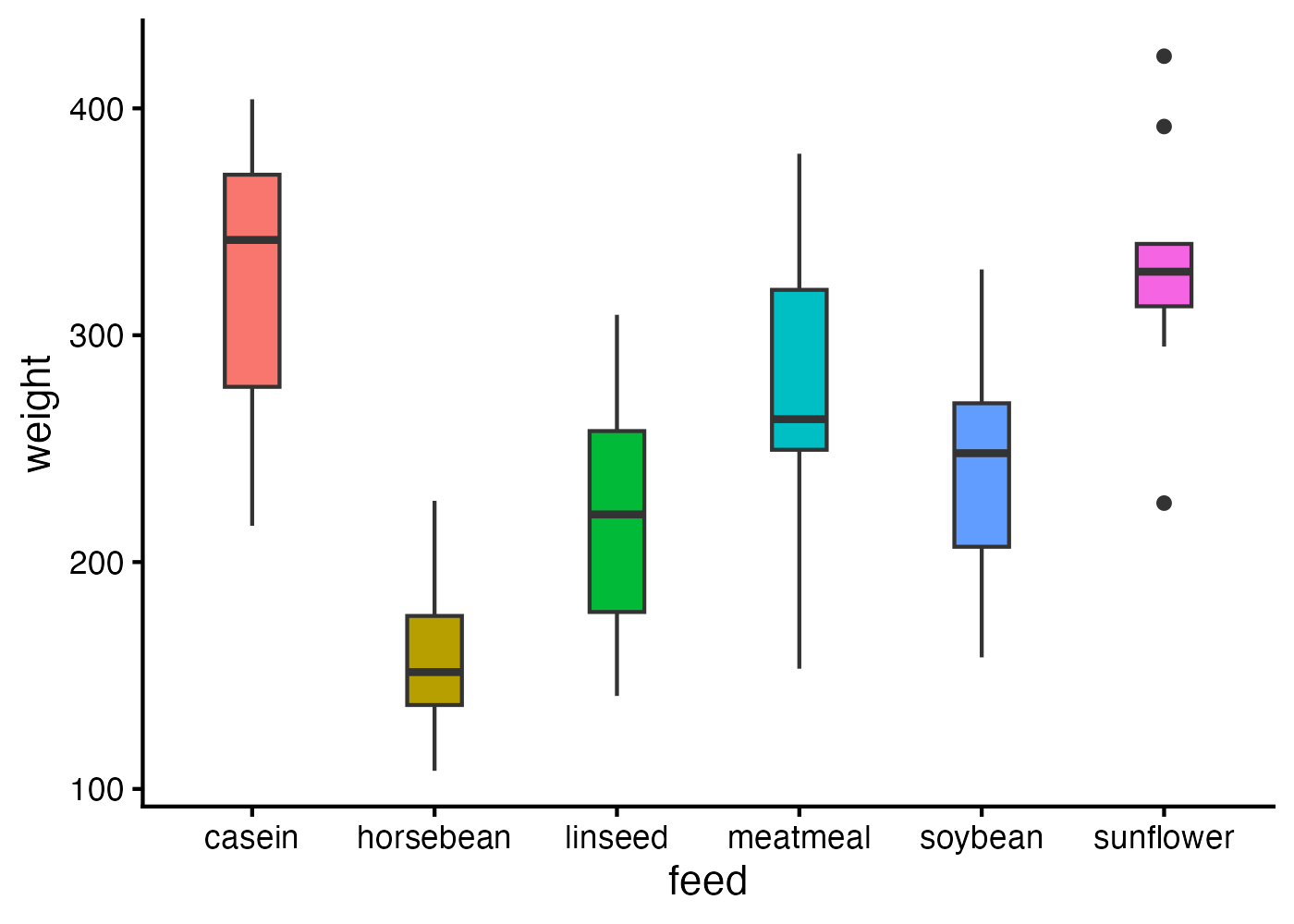


# オムニバス検定（between引数を指定する）
omni = afex::aov_ez(id = "id", dv = "weight", data = dat, between = "feed")
omni_eff = effectsize::eta_squared(omni, partial = TRUE)
omni_results = cbind(afex::nice(omni), omni_eff)

# 事後検定
post_emm = emmeans::emmeans(omni, ~ feed)
post = emmeans::contrast(post_emm, "pairwise", adjust = "tukey")
post_eff = emmeans::eff_size(post_emm, sigma = stats::sigma(omni$lm),
  edf = stats::df.residual(omni$lm), method = "pairwise")
post_results = cbind(summary(post, infer = TRUE), as.data.frame(post_eff))

オムニバス検定にはafex::aov_ez()関数を使います。主な引数：

id：参加者IDの列名
dv：従属変数の列名
data：データフレーム
between：被験者間要因の列名

結果を確認しましょう。

# オムニバス検定の結果
omni_results
##   Effect    df     MSE         F  ges p.value Parameter      Eta2   CI
## 1   feed 5, 65 3008.55 15.36 *** .542   <.001      feed 0.5416855 0.95
##      CI_low CI_high
## 1 0.3853879       1

オムニバス検定の結果、feed（餌の種類）に有意な効果が認められました。

統計検定量であるF値は F(5, 65) = 15.36、p値は p < .001、効果量は $\eta_p^2$ = .54 です。

なお、afex::nice(omni) を使うとp値が小さい場合は <.001 などのような概略値になります。具体的な値が知りたい場合は stats::anova(omni) を使ってください。

餌の主効果が有意だったので、多重比較を行います。以下がその結果です。

post_results
## 結果が長いので出力は省略

餌には6つの水準があるので、合計15のペア比較が行われています。p値が0.05未満である行のみを抽出して、有意差があったペアだけをわかりやすく表示させましょう。

# 列名の重複を解消する
names(post_results) = make.unique(names(post_results))
# 必要な情報のみを抽出
post_results %>%
  dplyr::filter(p.value < 0.05) %>% # 有意な列のみ抽出
  dplyr::select(c(1, 8, 10, 13:14)) # 必要な列のみ抽出
##                contrast      p.value effect.size lower.CL.1 upper.CL.1
## 1    casein - horsebean 3.070197e-08    2.978714  1.9769844  3.9804439
## 2      casein - linseed 2.100151e-04    1.911263  1.0298800  2.7926463
## 3      casein - soybean 8.365309e-03    1.406643  0.5832447  2.2300408
## 4  horsebean - meatmeal 1.062092e-04   -2.127775 -3.0766480 -1.1789026
## 5   horsebean - soybean 4.216654e-03   -1.572071 -2.4436097 -0.7005331
## 6 horsebean - sunflower 1.219887e-08   -3.075949 -4.0866539 -2.0652433
## 7   linseed - sunflower 8.843233e-05   -2.008497 -2.8964896 -1.1205054
## 8   soybean - sunflower 3.884521e-03   -1.503877 -2.3325310 -0.6752233

この8つの組み合わせにおいて有意差が見られたようです。グラフを中央値の順で並べ替えて、どのペアが有意差ありと判定されたのかを読み取りやすくしてみましょう。

ggplot(dat, aes(x = forcats::fct_reorder(
  feed, weight, median, .desc = FALSE), y = weight, fill = feed)) +
  geom_boxplot(width = 0.3) +
  labs(x = "feed") +
  theme_classic(base_size = 16) +
  theme(legend.position = "none")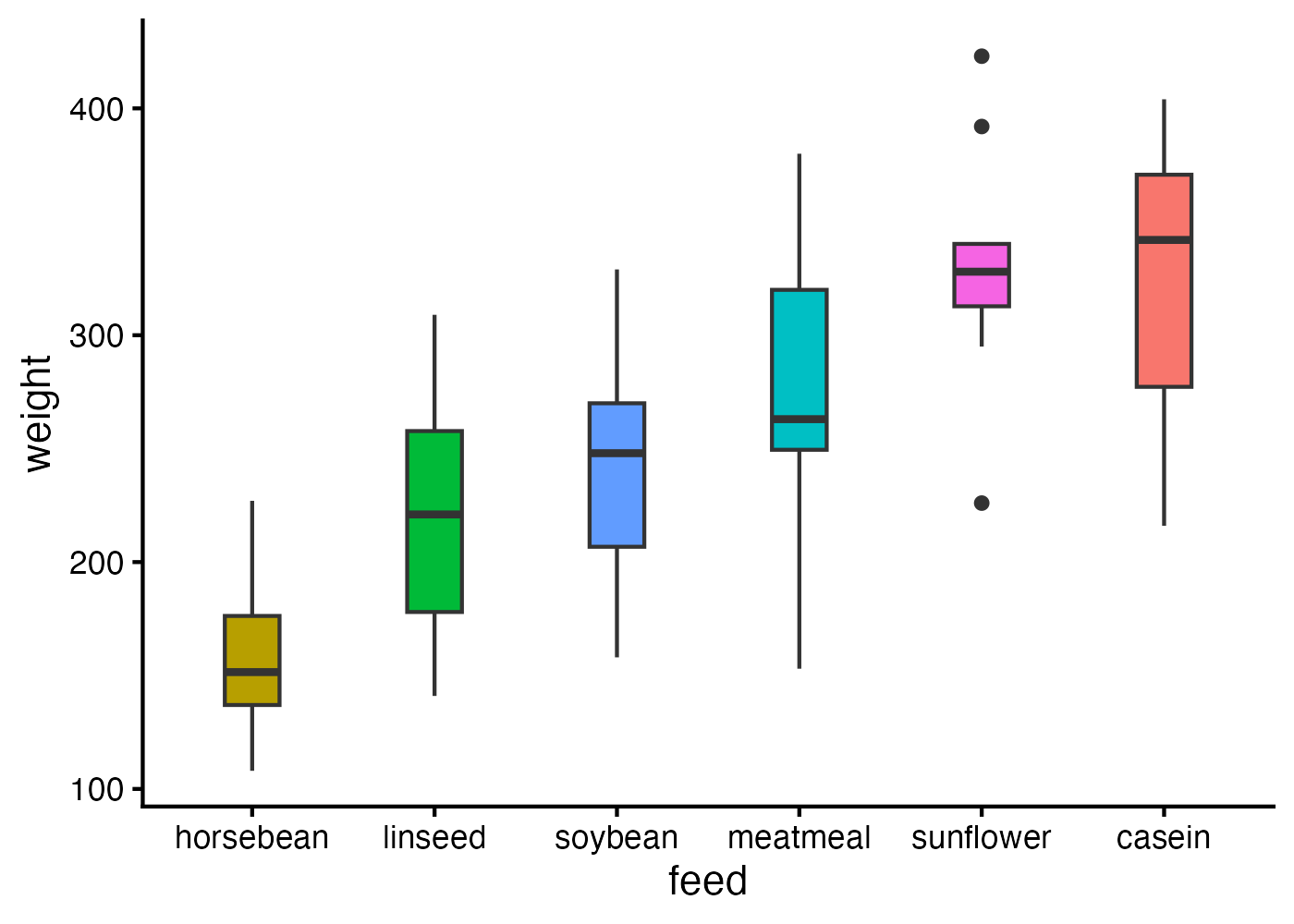

以上の結果を論文で報告する際は以下のように記述します。

餌の種類を独立変数とした1要因分散分析の結果、餌の種類の主効果は有意であった（F(5, 65) = 15.36, p < .001, $\eta_p^2$ = .54, 95% CI [0.38, 1.00]）。
Tukey法による多重比較の結果、次の水準間で有意差が見られた：casein と horsebean（p < .001, d = 2.98）、casein と linseed（p < .001, d = 1.91）、casein と soybean（p = .0084, d = 1.41）、horsebean と meatmeal（p < .001, d = -2.12）、horsebean と soybean（p = .0042, d = -1.57）、horsebean と sunflower（p < .001, d = -3.08）、linseed と sunflower（p < .001, d = -2.01）、soybean と sunflower（p < .001, d = -1.50）。これら以外の水準間では有意差はみられなかった（all ps > .05）。

［信頼区間］上記の記述例で、オムニバス検定では効果量の信頼区間も記述していますが、多重検定では信頼区間を省略しています。実際はどちらの場合でも書いた方がいいので、書くようにしましょう。例：casein と horsebean（p < .001, d = 2.98, 95% CI [1.98, 3.98]）

［p値の書き方］p値は有意差の有無にかかわらず具体的な数値を書くことが推奨されます（p < .05 とは書かずに p = .0084 などのように具体的な数値を書く）。ただし、0.001よりも小さい場合は p < .001 という表記をしても良いとされます。また、多量の非有意なp値をまとめて all ps > .05 といった表記で報告することもあります（ただしこれは非推奨であり、具体的なp値を書くのが原則です）。

［文章ではなく表にする］今回のように有意なペアが多い場合（あるいはそうでない場合でも）、非有意な結果も含め、すべての値を表にまとめて表示するのがわかりやすいかもしれません。

12.6.2 1要因分散分析（対応あり）

同じ参加者がその要因のすべての水準で測定される場合に用います。

以下の例ではオムニバス検定が有意なので、事後検定も行っています。

# データ
dat = data.frame(
  id = rep(paste0("s", 1:10), times = 3),
  cond = rep(c("A", "B", "C"), each = 10),
  score = c(rnorm(10, 50, 3), rnorm(10, 60, 5), rnorm(10, 63, 6))
)

# 可視化
fig = ggplot(dat, aes(x = cond, y = score, fill = cond)) +
    geom_boxplot(width = 0.3) +
    theme_classic(base_size = 16)
plot(fig)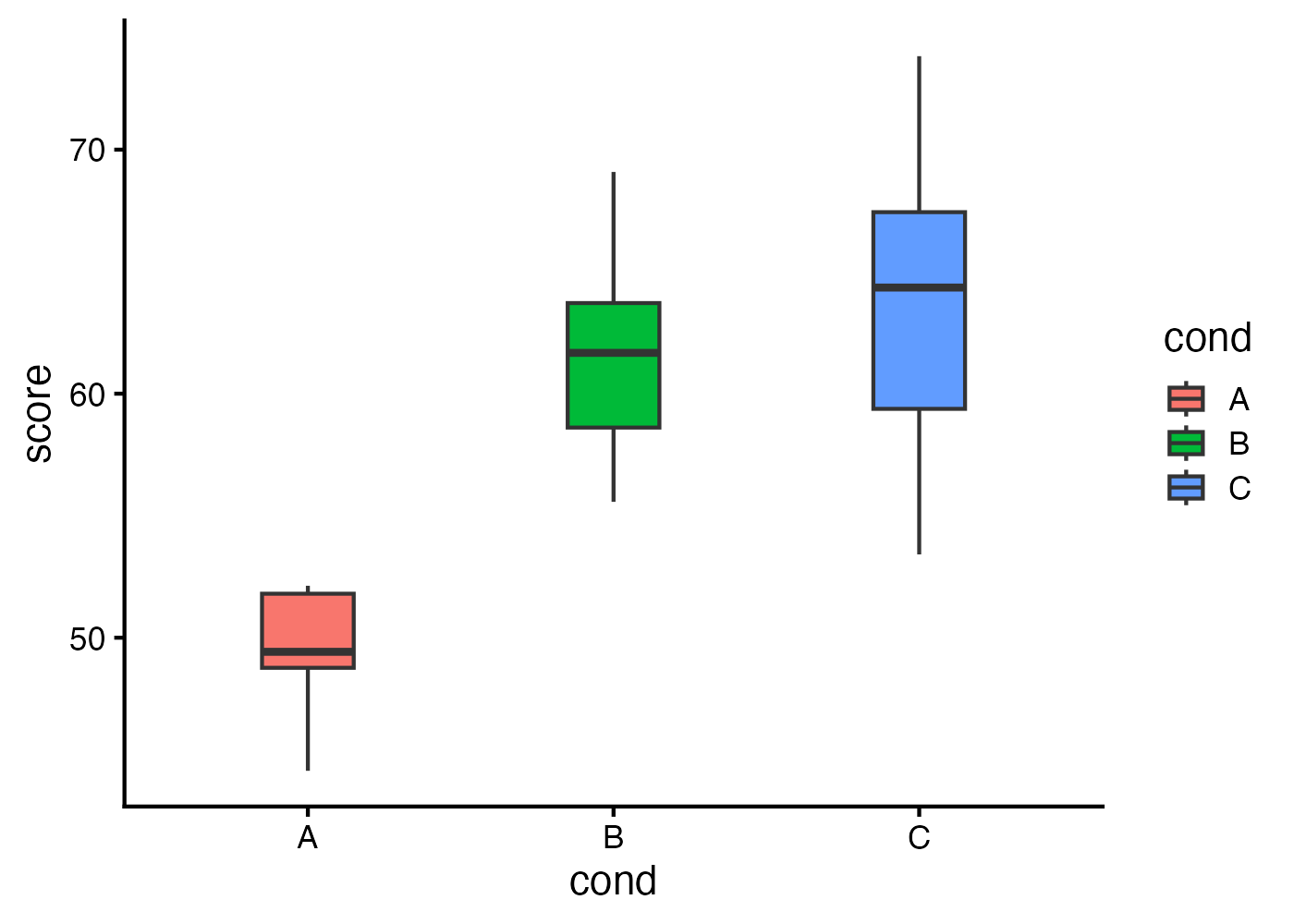

# オムニバス検定（within引数を指定する）
omni = afex::aov_ez("id", "score", dat, within = "cond")
omni_eff = effectsize::eta_squared(omni, partial = TRUE)
omni_results = cbind(afex::nice(omni), omni_eff)

# 事後検定
resid_mat = residuals(omni$lm)
edf = df.residual(omni$lm)
sigma_hat = sqrt(mean(colSums(resid_mat^2) / edf))
post_emm = emmeans::emmeans(omni, ~ cond)
post = emmeans::contrast(post_emm, "pairwise", adjust = "tukey")
post_eff = emmeans::eff_size(post, sigma = sigma_hat, edf = edf, method = "identity")
post_results = cbind(
  as.data.frame(summary(post, infer = TRUE)),
  as.data.frame(summary(post_eff))
)

対応あり（参加者内）デザインにおける事後検定の効果量算出について

対応のある要因を1つでも含む分散分析では、事後検定における効果量の計算が対応なしの場合とは異なります。

詳しい説明（クリックして展開）

問題の背景

emmeans::eff_size()関数で効果量（Cohen’s d）を算出するには、sigma（プールされた標準偏差）とedf（誤差自由度）を指定する必要があります。

対応なし分散分析や対応あり分散分析の単独の場合、これらの値は以下のように簡単に取得できます：

sigma = stats::sigma(omni$lm)
edf = stats::df.residual(omni$lm)

しかし、混合計画ではafex::aov_ez()が内部的に多変量線形モデル（mlmクラス）を使用するため、この方法が機能しません。

混合計画の誤差構造

混合計画では、2種類の誤差項が存在します：

被験者間誤差：異なる参加者間のばらつき（groupの効果を検定する際に使用）
被験者内誤差：同じ参加者内での時点間のばらつき（timeの効果を検定する際に使用）

afex::aov_ez()は被験者内要因を含む場合、データを「参加者 × 時点」の行列形式で扱う多変量アプローチを採用します。

そのため、omni$lmは通常のlmオブジェクトではなくmlm（multivariate linear model）クラスになります。

class(omni$lm)
## [1] "mlm" "lm"

mlmオブジェクトでは、stats::sigma()が単一の値を返さず、emmeans::eff_size()が期待する形式と合致しないためエラーが発生します。

解決策

残差行列から直接プールされた標準偏差を算出します：

resid_mat = residuals(omni$lm)  # 参加者 × 要因の行列
edf = df.residual(omni$lm)      # 誤差自由度（スカラー）
sigma_hat = sqrt(mean(colSums(resid_mat^2) / edf))

この計算の意味は以下のとおりです：

residuals(omni$lm)：各参加者・各時点の残差を行列形式で取得
colSums(resid_mat^2)：各時点（列）の残差平方和を算出
… / edf：各時点の残差分散を算出
mean(…)：時点間で残差分散を平均（プール）
sqrt(…)：標準偏差に変換

この方法により、混合計画における被験者内変動を適切に反映したプールされた標準偏差が得られます。

method = “identity”について

eff_size()に渡すオブジェクトの種類によって、method引数の指定が変わります：

emmeansオブジェクトを渡す場合：method = “pairwise”などを指定し、関数内部でペアワイズ比較を行う
contrastオブジェクトを渡す場合：method = “identity”を指定し、すでに計算された対比をそのまま使用

混合計画では、contrastオブジェクトを渡してmethod = “identity”とする方が安定して動作します。

12.6.3 2要因（どちらの要因も対応なし）

2要因の対応なし分散分析は、2つの独立した要因がある場合に使用します。

要因分散分析では、以下の3つの効果を検定します：

Aの主効果：要因Bの水準を無視したとき、Aの水準間に差があるか
Bの主効果：要因Aの水準を無視したとき、Bの水準間に差があるか
A×Bの交互作用：一方の要因の効果が、他方の要因の水準によって異なるか

交互作用が有意な場合、主効果の解釈には注意が必要です。交互作用がある場合、「Aの効果はBの水準によって異なる」ため、Aの主効果を単純に解釈することは適切ではありません。このような場合は、単純主効果の検定を行います。

# データ
dat = datasets::ToothGrowth
dat$id = as.factor(1:nrow(dat))
names(dat) = c("score", "supp", "dose", "id")
dat$dose = as.factor(dat$dose)

# 可視化
fig = ggplot(dat, aes(x = supp, y = score, fill = dose)) +
  geom_boxplot(width = 0.3, position = position_dodge(width = 0.6)) +
  theme_classic(base_size = 16)
plot(fig)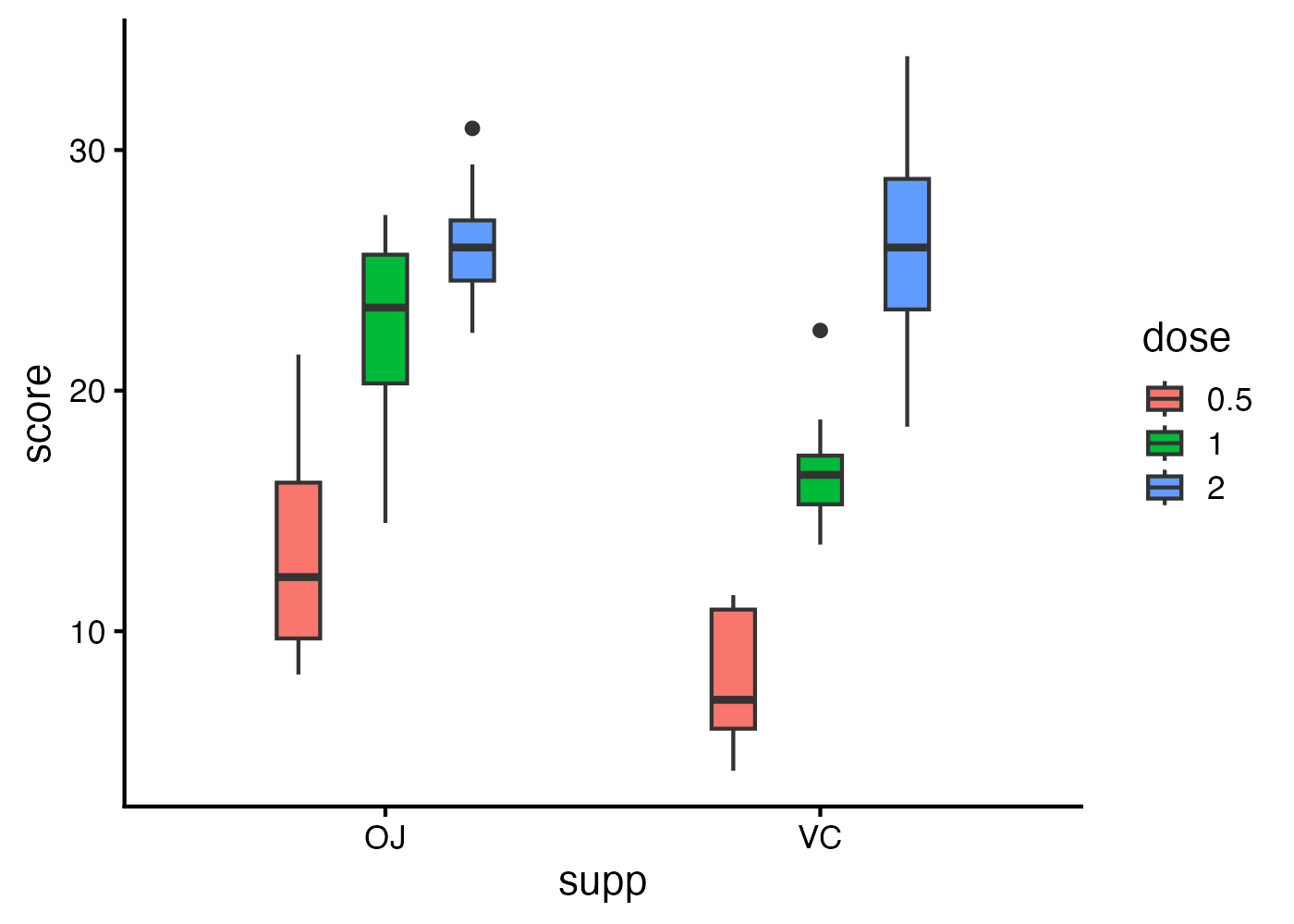

# オムニバス検定（between引数に2つの要因を指定）
omni = afex::aov_ez("id", "score", dat, between = c("supp", "dose"))
omni_eff = effectsize::eta_squared(omni, partial = TRUE)
omni_results = cbind(afex::nice(omni), as.data.frame(omni_eff))

# 交互作用が有意だった場合の単純主効果検定
## suppの各水準におけるdoseの単純主効果（オムニバス）
simple_omni_1 = emmeans::joint_tests(omni, by = "supp")
simple_omni_1_eff = effectsize::F_to_eta2(
  f = simple_omni_1$F.ratio, df = simple_omni_1$df1,
  df_error = simple_omni_1$df2, ci = 0.95)
simple_omni_1_results = cbind(as.data.frame(simple_omni_1), as.data.frame(simple_omni_1_eff))
## suppの各水準におけるdoseの多重比較
post_emm_1 = emmeans::emmeans(omni, ~ dose | supp)
post_1 = emmeans::contrast(post_emm_1, "pairwise", adjust = "tukey")
post_1_eff = emmeans::eff_size(post_emm_1, sigma = stats::sigma(omni$lm),
  edf = stats::df.residual(omni$lm), method = "pairwise")
post_1_results = cbind(summary(post_1, infer = TRUE), as.data.frame(post_1_eff))
## doseの各水準におけるsuppの単純主効果（オムニバス）
simple_omni_2 = emmeans::joint_tests(omni, by = "dose")
simple_omni_2_eff = effectsize::F_to_eta2(
  f = simple_omni_2$F.ratio, df = simple_omni_2$df1,
  df_error = simple_omni_2$df2, ci = 0.95)
simple_omni_2_results = cbind(as.data.frame(simple_omni_2), as.data.frame(simple_omni_2_eff))
## doseの各水準におけるsuppの多重比較
post_emm_2 = emmeans::emmeans(omni, ~ supp | dose)
post_2 = emmeans::contrast(post_emm_2, "pairwise", adjust = "tukey")
post_2_eff = emmeans::eff_size(post_emm_2, sigma = stats::sigma(omni$lm),
  edf = stats::df.residual(omni$lm), method = "pairwise")
post_2_results = cbind(summary(post_2, infer = TRUE), as.data.frame(post_2_eff))

# （参考）交互作用が有意でない場合
## doseの主効果
main_1_emm = emmeans::emmeans(omni, ~ dose)
main_1 = emmeans::contrast(main_1_emm, "pairwise", adjust = "tukey")
main_1_eff = emmeans::eff_size(main_1_emm, sigma = stats::sigma(omni$lm), 
  edf = stats::df.residual(omni$lm), method = "pairwise")
main_1_results = cbind(summary(main_1, infer = TRUE), as.data.frame(main_1_eff))
## suppの主効果
main_2_emm = emmeans::emmeans(omni, ~ supp)
main_2 = emmeans::contrast(main_2_emm, "pairwise", adjust = "tukey")
main_2_eff = emmeans::eff_size(main_2_emm, sigma = stats::sigma(omni$lm), 
  edf = stats::df.residual(omni$lm), method = "pairwise")
main_2_results = cbind(summary(main_2, infer = TRUE), as.data.frame(main_2_eff))

12.6.4 2要因（どちらの要因も対応あり）

2要因の対応あり分散分析は、同じ参加者が両方の要因のすべての水準を経験するタイプのデザインです。たとえば、同じ参加者が異なる課題条件（要因A）と異なる時間条件（要因B）のすべての組み合わせで測定されるような場合に使用します。

# データ
set.seed(12345)
n = 30  # 参加者数
dat = expand.grid(
  id = factor(1:n),
  task = factor(c("easy", "medium", "hard"), levels = c("easy", "medium", "hard")),
  time = factor(c("morning", "evening"), levels = c("morning", "evening"))
)
dat$score = with(dat,
  50 +
  ifelse(task == "medium", -5, ifelse(task == "hard", -15, 0)) +
  ifelse(time == "evening", -3, 0) +
  ifelse(task == "hard" & time == "evening", -8, 0) +  # 交互作用
  rnorm(nrow(dat), 0, 8) +
  rep(rnorm(n, 0, 7), each = 6)  # 個人差
)

# 可視化
fig = ggplot(dat, aes(x = task, y = score, fill = time)) +
  geom_boxplot(width = 0.3, position = position_dodge(width = 0.6)) +
  theme_classic(base_size = 16)
plot(fig)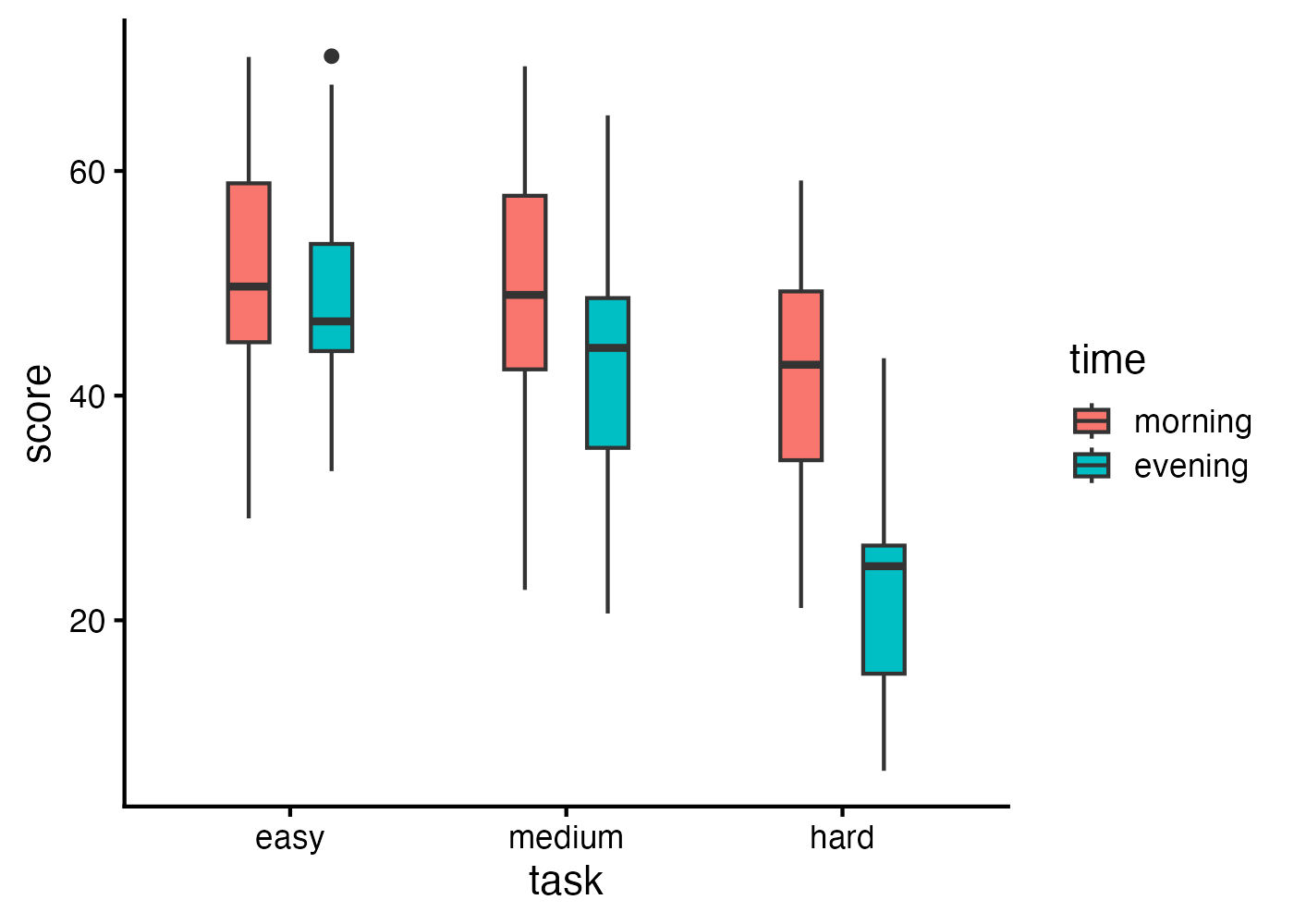

# オムニバス検定（within引数に2つの要因を指定）
omni = afex::aov_ez("id", "score", dat, within = c("task", "time"))
omni_eff = effectsize::eta_squared(omni, partial = TRUE, ci = 0.95)
omni_results = cbind(afex::nice(omni), as.data.frame(omni_eff))

# 効果量算出のためのsigmaとedfを準備
resid_mat = residuals(omni$lm)
edf = df.residual(omni$lm)
sigma_hat = sqrt(mean(colSums(resid_mat^2) / edf))

# 交互作用が有意だった場合の単純主効果検定
## taskの各水準におけるtimeの単純主効果（オムニバス）
simple_omni_1 = emmeans::joint_tests(omni, by = "task")
simple_omni_1_eff = effectsize::F_to_eta2(
  f = simple_omni_1$F.ratio, df = simple_omni_1$df1,
  df_error = simple_omni_1$df2, ci = 0.95)
simple_omni_1_results = cbind(as.data.frame(simple_omni_1), as.data.frame(simple_omni_1_eff))
## taskの各水準におけるtimeの多重比較（2水準なのでこのデータでは不要）
post_emm_1 = emmeans::emmeans(omni, ~ time | task)
post_1 = emmeans::contrast(post_emm_1, "pairwise", adjust = "tukey")
post_1_eff = emmeans::eff_size(post_1, sigma = sigma_hat, edf = edf, method = "identity")
post_1_results = cbind(
  as.data.frame(summary(post_1, infer = TRUE)),
  as.data.frame(summary(post_1_eff))
)
## timeの各水準におけるtaskの単純主効果（オムニバス）
simple_omni_2 = emmeans::joint_tests(omni, by = "time")
simple_omni_2_eff = effectsize::F_to_eta2(
  f = simple_omni_2$F.ratio, df = simple_omni_2$df1,
  df_error = simple_omni_2$df2, ci = 0.95)
simple_omni_2_results = cbind(as.data.frame(simple_omni_2), as.data.frame(simple_omni_2_eff))
## timeの各水準におけるtaskの多重比較
post_emm_2 = emmeans::emmeans(omni, ~ task | time)
post_2 = emmeans::contrast(post_emm_2, "pairwise", adjust = "tukey")
post_2_eff = emmeans::eff_size(post_2, sigma = sigma_hat, edf = edf, method = "identity")
post_2_results = cbind(
  as.data.frame(summary(post_2, infer = TRUE)),
  as.data.frame(summary(post_2_eff))
)

# （参考）交互作用が有意でない場合
## taskの主効果
main_1_emm = emmeans::emmeans(omni, ~ task)
main_1 = emmeans::contrast(main_1_emm, "pairwise", adjust = "tukey")
main_1_eff = emmeans::eff_size(main_1, sigma = sigma_hat, edf = edf, method = "identity")
main_1_results = cbind(
  as.data.frame(summary(main_1, infer = TRUE)),
  as.data.frame(summary(main_1_eff))
)
## timeの主効果
main_2_emm = emmeans::emmeans(omni, ~ time)
main_2 = emmeans::contrast(main_2_emm, "pairwise", adjust = "tukey")
main_2_eff = emmeans::eff_size(main_2, sigma = sigma_hat, edf = edf, method = "identity")
main_2_results = cbind(
  as.data.frame(summary(main_2, infer = TRUE)),
  as.data.frame(summary(main_2_eff))
)

12.6.5 2要因・混合計画（被験者間 × 被験者内）

混合計画は、対応なし（被験者間）の要因と対応あり（被験者内）の要因の両方を含むデザインです。

# データ
dat = data.frame(
  id = rep(paste0("s", 1:20), each = 3),
  group = rep(c("Control", "Exp"), each = 30),
  time = rep(c("Pre", "Post", "Follow"), 20),
  score = NA
)
dat$score = with(dat, rnorm(n = nrow(dat), mean = ifelse(
  group == "Control", 50, ifelse(time == "Pre", 50, ifelse(time == "Post", 65, 60))),
  sd = 5))
dat$id = factor(dat$id)
dat$group = factor(dat$group, levels = c("Control", "Exp"))
dat$time = factor(dat$time, levels = c("Pre", "Post", "Follow"))

# 可視化
fig = ggplot(dat, aes(x = group, y = score, fill = time)) +
    geom_boxplot(width = 0.3, position = position_dodge(width = 0.6)) +
    theme_classic(base_size = 16)
plot(fig)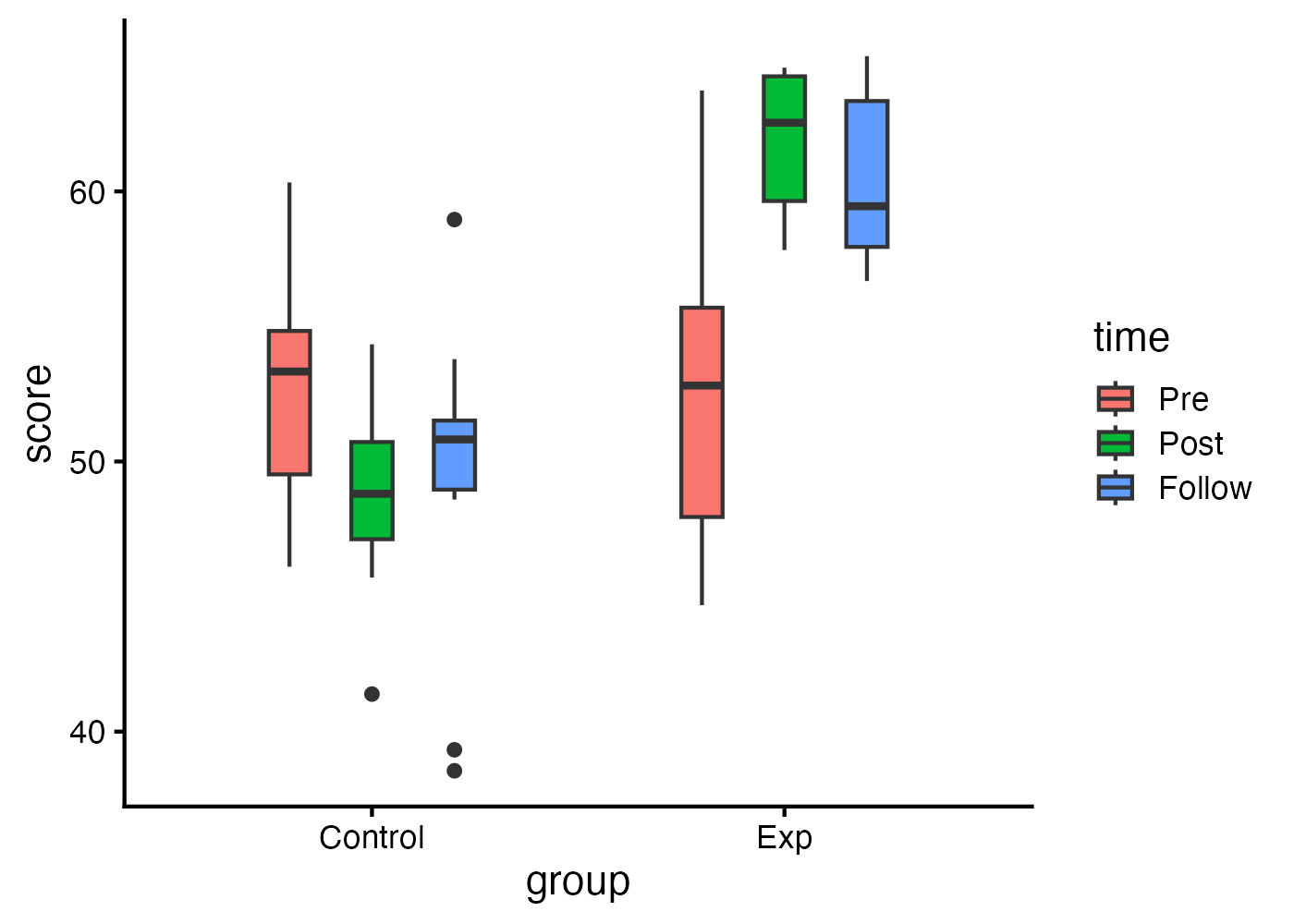

# オムニバス検定（between と within を両方指定）
omni = afex::aov_ez("id", "score", dat, between = "group", within = "time")
omni_eff = effectsize::eta_squared(omni, partial = TRUE)
omni_results = cbind(afex::nice(omni), as.data.frame(omni_eff))

# 事後検定に必要な値の計算
edf = df.residual(omni$lm)
sigma_hat = sqrt(mean(colSums(residuals(omni$lm)^2) / edf))

# 交互作用が有意だった場合の単純主効果検定
## groupの各水準におけるtimeの単純主効果（オムニバス）
simple_omni_1 = emmeans::joint_tests(omni, by = "group")
simple_omni_1_eff = effectsize::F_to_eta2(
  f = simple_omni_1$F.ratio, df = simple_omni_1$df1,
  df_error = simple_omni_1$df2, ci = 0.95)
simple_omni_1_results = cbind(as.data.frame(simple_omni_1), as.data.frame(simple_omni_1_eff))
## groupの各水準におけるtimeの多重比較
post_emm_1 = emmeans::emmeans(omni, ~ time | group)
post_1 = emmeans::contrast(post_emm_1, "pairwise", adjust = "tukey")
post_1_eff = emmeans::eff_size(post_1, sigma = sigma_hat, edf = edf, method = "identity")
post_1_results = cbind(summary(post_1, infer = TRUE), as.data.frame(post_1_eff))
## timeの各水準におけるgroupの単純主効果（オムニバス）
simple_omni_2 = emmeans::joint_tests(omni, by = "time")
simple_omni_2_eff = effectsize::F_to_eta2(
  f = simple_omni_2$F.ratio, df = simple_omni_2$df1,
  df_error = simple_omni_2$df2, ci = 0.95)
simple_omni_2_results = cbind(as.data.frame(simple_omni_2), as.data.frame(simple_omni_2_eff))
## timeの各水準におけるgroupの多重比較
post_emm_2 = emmeans::emmeans(omni, ~ group | time)
post_2 = emmeans::contrast(post_emm_2, "pairwise", adjust = "tukey")
post_2_eff = emmeans::eff_size(post_2, sigma = sigma_hat, edf = edf, method = "identity")
post_2_results = cbind(summary(post_2, infer = TRUE), as.data.frame(post_2_eff))

# （参考）交互作用が有意でない場合
## timeの主効果
main_1_emm = emmeans::emmeans(omni, ~ time)
main_1 = emmeans::contrast(main_1_emm, "pairwise", adjust = "tukey")
main_1_eff = emmeans::eff_size(main_1, sigma = sigma_hat, edf = edf, method = "identity")
main_1_results = cbind(summary(main_1, infer = TRUE), as.data.frame(main_1_eff))
## groupの主効果
main_2_emm = emmeans::emmeans(omni, ~ group)
main_2 = emmeans::contrast(main_2_emm, "pairwise", adjust = "tukey")
main_2_eff = emmeans::eff_size(main_2, sigma = sigma_hat, edf = edf, method = "identity")
main_2_results = cbind(summary(main_2, infer = TRUE), as.data.frame(main_2_eff))

12.6.6 3要因以上の分散分析

3要因以上の分散分析も、基本的な考え方は2要因の場合と同じです。ただし、交互作用の数が増えるため、結果の解釈がより複雑になります。

3要因分散分析では、以下の効果を検定します：

3つの主効果（A, B, C）
3つの2次交互作用（A:B, A:C, B:C）
1つの3次交互作用（A:B:C）

結果の解釈の方針

3要因分散分析の結果は、以下の順序で解釈します：

3次交互作用（A:B:C）が有意な場合：1つの要因の各水準で、残り2要因の単純交互作用を検定します。これは2要因分散分析を複数回行うことに相当します。
3次交互作用が有意でなく、2次交互作用が有意な場合：該当する2要因の組み合わせについて単純主効果を検定します。
交互作用がすべて有意でない場合：各主効果について事後検定を行います。

オムニバス検定のスクリプト例

以下に、3要因分散分析のオムニバス検定までのスクリプトを示します。各パターンの対応の有無に応じたコード例を掲載します。

# オムニバス検定
## パターン1：3要因すべて対応なし
omni = afex::aov_ez("id", "score", dat, between = c("A", "B", "C"))
## パターン2：Cのみ対応あり（A, Bは対応なし）
omni = afex::aov_ez("id", "score", dat, between = c("A", "B"), within = "C")
## パターン3：BとCが対応あり（Aのみ対応なし）
omni = afex::aov_ez("id", "score", dat, between = "A", within = c("B", "C"))
## パターン4：3要因すべて対応あり
omni = afex::aov_ez("id", "score", dat, within = c("A", "B", "C"))
## オムニバス検定の効果量の計算
omni_eff = effectsize::eta_squared(omni, partial = TRUE, ci = 0.95)
omni_results = cbind(anova(omni), as.data.frame(omni_eff))

事後検定の進め方

オムニバス検定の後、交互作用の有意性に応じて事後検定を行います。事後検定の具体的な方法は、層別化した後の2要因の組み合わせによって異なります。以下を参考に、該当するセクションを参照してください。

3次交互作用（A:B:C）が有意な場合

1つの要因で層別化し、残り2要因の交互作用を分析します。この分析は通常の2要因分散分析と同じ手順で実施できます。どの分析手順を用いるかは残り2要因の対応によって変わります。

残りの2要因がどちらも対応なし：2要因（どちらも対応なし）の分散分析を行う
残りの2要因がどちらも対応あり：2要因（どちらも対応あり）の分散分析を行う
残りの2要因が混合計画　　　　：2要因（混合計画）の分散分析を行う

2次交互作用（A:B, A:C, B:C）が有意な場合

該当する有意な2要因の組み合わせについて単純主効果を検定します。参照するセクションは、その2要因の対応の有無によって決まります。

2要因がどちらも対応なし：2要因（どちらも対応なし）の分散分析を行う
2要因がどちらも対応あり：2要因（どちらも対応あり）の分散分析を行う
2要因が混合計画　　　　：2要因（混合計画）の分散分析を行う

補足：3次交互作用と2次交互作用の両方が有意な場合

オムニバス検定を実施した際に、3次の交互作用（A:B:C）が有意で、さらに2次の交互作用（たとえばA:Bのみ）が有意であったとします。3次交互作用が有意であるということは、「A:Bの交互作用のパターンがCの水準によって異なる」ことを意味します。

この場合、オムニバス検定で見られたA:Bの2次交互作用をそのまま解釈することはできません。Cの要因ごとに残り2要因（A:B）の交互作用を分析する必要があります。

事後検定のコード例

3次交互作用が有意で、要因Cの各水準でA×Bの単純交互作用を検定する例を示します。

コード例（クリックして展開）

# データ（3要因混合計画: A, Bが被験者間、Cが被験者内）
set.seed(123)
n = 30
dat = expand.grid(
  subj = 1:n,
  A = c("a1", "a2"),
  B = c("b1", "b2"),
  C = c("c1", "c2", "c3")
)
dat$id = factor(paste(dat$A, dat$B, dat$subj, sep = "_"))
dat$A = factor(dat$A)
dat$B = factor(dat$B)
dat$C = factor(dat$C, levels = c("c1", "c2", "c3"))
dat$score = with(dat,
  50 +
  ifelse(A == "a2", 5, 0) +
  ifelse(B == "b2", 3, 0) +
  ifelse(C == "c2", 4, ifelse(C == "c3", 8, 0)) +
  ifelse(A == "a2" & B == "b2" & C == "c3", 10, 0) +  # 3次交互作用
  rnorm(nrow(dat), 0, 6) +
  rep(rnorm(n * 4, 0, 3), each = 3)
)
dat = dat[, c("id", "A", "B", "C", "score")]

# オムニバス検定
omni = afex::aov_ez("id", "score", dat, between = c("A", "B"), within = "C")
omni_eff = effectsize::eta_squared(omni, partial = TRUE, ci = 0.95)
omni_results = cbind(anova(omni), as.data.frame(omni_eff))
print(omni_results)

# 効果量算出のためのsigmaとedfを準備（被験者内要因を含む場合）
resid_mat = as.matrix(residuals(omni$lm))
edf = df.residual(omni$lm)
sigma_hat = sqrt(mean(colSums(resid_mat^2) / edf))

# -------------------------------------------
# 3次交互作用（A:B:C）が有意な場合の分析
# -------------------------------------------

# Cの各水準におけるA×Bの単純交互作用（オムニバス）
simple_int = emmeans::joint_tests(omni, by = "C")
simple_int_eff = effectsize::F_to_eta2(
  f = simple_int$F.ratio, df = simple_int$df1,
  df_error = simple_int$df2, ci = 0.95)
simple_int_results = cbind(as.data.frame(simple_int), as.data.frame(simple_int_eff))
print(simple_int_results)

# -------------------------------------------
# あるCの水準でA:Bの単純交互作用が有意な場合
# その水準において、AまたはBで層別化して単純主効果を検定
# -------------------------------------------

# 例：C = c1において、Aの各水準におけるBの単純主効果（オムニバス）
simple_omni_B = emmeans::joint_tests(omni, by = "A", at = list(C = "c1"))
simple_omni_B_eff = effectsize::F_to_eta2(
  f = simple_omni_B$F.ratio, df = simple_omni_B$df1,
  df_error = simple_omni_B$df2, ci = 0.95)
simple_omni_B_results = cbind(as.data.frame(simple_omni_B), as.data.frame(simple_omni_B_eff))
print(simple_omni_B_results)

# 例：C = c1において、Aの各水準におけるBの多重比較
emm_B = emmeans::emmeans(omni, ~ B | A, at = list(C = "c1"))
post_B = emmeans::contrast(emm_B, "pairwise", adjust = "tukey")
post_B_eff = emmeans::eff_size(post_B, sigma = sigma_hat, edf = edf, method = "identity")
post_B_results = cbind(
  as.data.frame(summary(post_B, infer = TRUE)),
  as.data.frame(summary(post_B_eff))
)
print(post_B_results)

# 例：C = c1において、Bの各水準におけるAの単純主効果（オムニバス）
simple_omni_A = emmeans::joint_tests(omni, by = "B", at = list(C = "c1"))
simple_omni_A_eff = effectsize::F_to_eta2(
  f = simple_omni_A$F.ratio, df = simple_omni_A$df1,
  df_error = simple_omni_A$df2, ci = 0.95)
simple_omni_A_results = cbind(as.data.frame(simple_omni_A), as.data.frame(simple_omni_A_eff))
print(simple_omni_A_results)

# 例：C = c1において、Bの各水準におけるAの多重比較
emm_A = emmeans::emmeans(omni, ~ A | B, at = list(C = "c1"))
post_A = emmeans::contrast(emm_A, "pairwise", adjust = "tukey")
post_A_eff = emmeans::eff_size(post_A, sigma = sigma_hat, edf = edf, method = "identity")
post_A_results = cbind(
  as.data.frame(summary(post_A, infer = TRUE)),
  as.data.frame(summary(post_A_eff))
)
print(post_A_results)

# -------------------------------------------
# ある水準でA:Bの単純交互作用が有意でない場合
# その水準において、AとBの主効果をそれぞれ検定
# -------------------------------------------

# 例：C = c2におけるAの主効果（オムニバス）
main_omni_A = emmeans::joint_tests(omni, at = list(C = "c2"))
main_omni_A = main_omni_A[main_omni_A$`model term` == "A", ]
main_omni_A_eff = effectsize::F_to_eta2(
  f = main_omni_A$F.ratio, df = main_omni_A$df1,
  df_error = main_omni_A$df2, ci = 0.95)
main_omni_A_results = cbind(as.data.frame(main_omni_A), as.data.frame(main_omni_A_eff))
print(main_omni_A_results)

# 例：C = c2におけるAの多重比較
emm_A_c2 = emmeans::emmeans(omni, ~ A, at = list(C = "c2"))
post_A_c2 = emmeans::contrast(emm_A_c2, "pairwise", adjust = "tukey")
post_A_c2_eff = emmeans::eff_size(post_A_c2, sigma = sigma_hat, edf = edf, method = "identity")
post_A_c2_results = cbind(
  as.data.frame(summary(post_A_c2, infer = TRUE)),
  as.data.frame(summary(post_A_c2_eff))
)
print(post_A_c2_results)

# 例：C = c2におけるBの主効果（オムニバス）
main_omni_B = emmeans::joint_tests(omni, at = list(C = "c2"))
main_omni_B = main_omni_B[main_omni_B$`model term` == "B", ]
main_omni_B_eff = effectsize::F_to_eta2(
  f = main_omni_B$F.ratio, df = main_omni_B$df1,
  df_error = main_omni_B$df2, ci = 0.95)
main_omni_B_results = cbind(as.data.frame(main_omni_B), as.data.frame(main_omni_B_eff))
print(main_omni_B_results)

# 例：C = c2におけるBの多重比較
emm_B_c2 = emmeans::emmeans(omni, ~ B, at = list(C = "c2"))
post_B_c2 = emmeans::contrast(emm_B_c2, "pairwise", adjust = "tukey")
post_B_c2_eff = emmeans::eff_size(post_B_c2, sigma = sigma_hat, edf = edf, method = "identity")
post_B_c2_results = cbind(
  as.data.frame(summary(post_B_c2, infer = TRUE)),
  as.data.frame(summary(post_B_c2_eff))
)
print(post_B_c2_results)

12.7 非パラメトリック分散分析

データが正規分布に従わない場合や順位データの場合、あるいはサンプルサイズが小さく正規性の仮定が満たされているか判断が難しい場合には、非パラメトリック検定を使用します。非パラメトリック検定は順位に基づいて検定を行うため、外れ値の影響を受けにくいという特徴があります。

このセクションでは、1要因の非パラメトリック検定にはrstatixパッケージを、多要因の非パラメトリック検定にはARToolパッケージを使用します。

library(tidyverse)
library(rstatix)
library(effectsize)
library(ARTool)
library(emmeans)

12.7.1 1要因（対応なし）の非パラメトリック：Kruskal-Wallis検定

Kruskal-Wallis検定は、対応のない1要因分散分析のノンパラメトリック版です。3群以上の独立したグループ間で、順位の分布に差があるかどうかを検定します。

使用する関数：

rstatix::kruskal_test()：Kruskal-Wallis検定を実行
rstatix::kruskal_effsize()：η²（H統計量に基づく効果量）を算出
rstatix::dunn_test()：Dunn検定による多重比較を実行
effectsize::rank_biserial：各ペアのrank-biserial correlationを算出

# データ
dat = data.frame(
  id = factor(1:45),
  group = factor(rep(c("A", "B", "C"), each = 15)),
  score = c(
    rexp(15, rate = 0.12), rexp(15, rate = 0.08), rexp(15, rate = 0.03))
)

# 可視化
fig = ggplot(dat, aes(x = group, y = score, fill = group)) +
    geom_boxplot(width = 0.3, position = position_dodge(width = 0.6)) +
    theme_classic(base_size = 16)
plot(fig)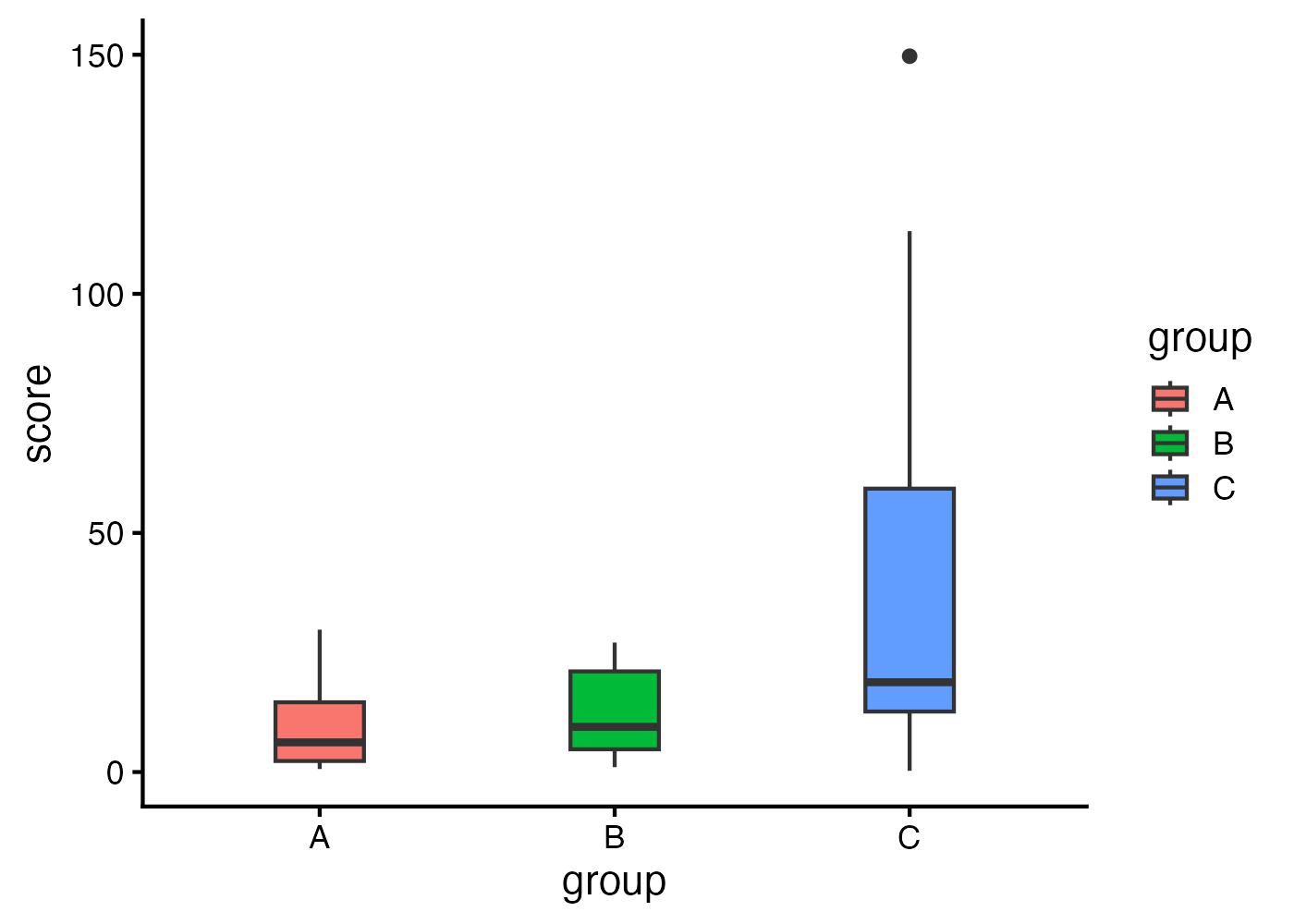


# オムニバス検定
omni = rstatix::kruskal_test(dat, score ~ group)

# オムニバス検定の効果量（η²）
# 信頼区間を計算したい場合は引数に ci = TRUE を加える。
omni_eff = rstatix::kruskal_effsize(dat, score ~ group)

# 事後検定（Dunn検定）
post = rstatix::dunn_test(dat, score ~ group, p.adjust.method = "holm")

# 事後検定の効果量（rank-biserial correlation）
groups = levels(dat$group)
pairs = combn(groups, 2, simplify = FALSE)
post_eff = lapply(pairs, function(pair) {
  sub = dat[dat$group %in% pair, ]
  sub$group = factor(sub$group, levels = pair)
  eff = effectsize::rank_biserial(score ~ group, data = sub, ci = 0.95)
  data.frame(
    group1 = pair[1], group2 = pair[2],
    r = eff$r_rank_biserial, r_CI_low = eff$CI_low, r_CI_high = eff$CI_high)
})
post_eff = do.call(rbind, post_eff)

# 結果の結合
post_results = merge(post, post_eff, by = c("group1", "group2"))

12.7.2 1要因（対応あり）の非パラメトリック：Friedman検定

Friedman検定は、対応のある1要因分散分析のノンパラメトリック版です。同じ参加者が複数の条件で測定された場合に使用します。

使用する関数：

rstatix::friedman_test()：Friedman検定を実行。式はscore ~ time | idの形式で、|の後に参加者IDを指定
rstatix::friedman_effsize()：効果料としてKendall’s Wを算出
rstatix::wilcox_test(…, paired = TRUE)：対応のあるWilcoxon符号付順位検定による多重比較
effectsize::rank_biserial：各ペアのrank-biserial correlationを算出

# データ
n = 20
dat = data.frame(
  id = factor(rep(1:n, times = 4)),
  time = factor(rep(c("t1", "t2", "t3", "t4"), each = n), 
                levels = c("t1", "t2", "t3", "t4")),
  score = c(rexp(n, rate = 0.10), rexp(n, rate = 0.08) + 2,
            rexp(n, rate = 0.06) + 4, rexp(n, rate = 0.05) + 6)
)

# 可視化
fig = ggplot(dat, aes(x = time, y = score, fill = time)) +
    geom_boxplot(width = 0.3, position = position_dodge(width = 0.6)) +
    theme_classic(base_size = 16)
plot(fig)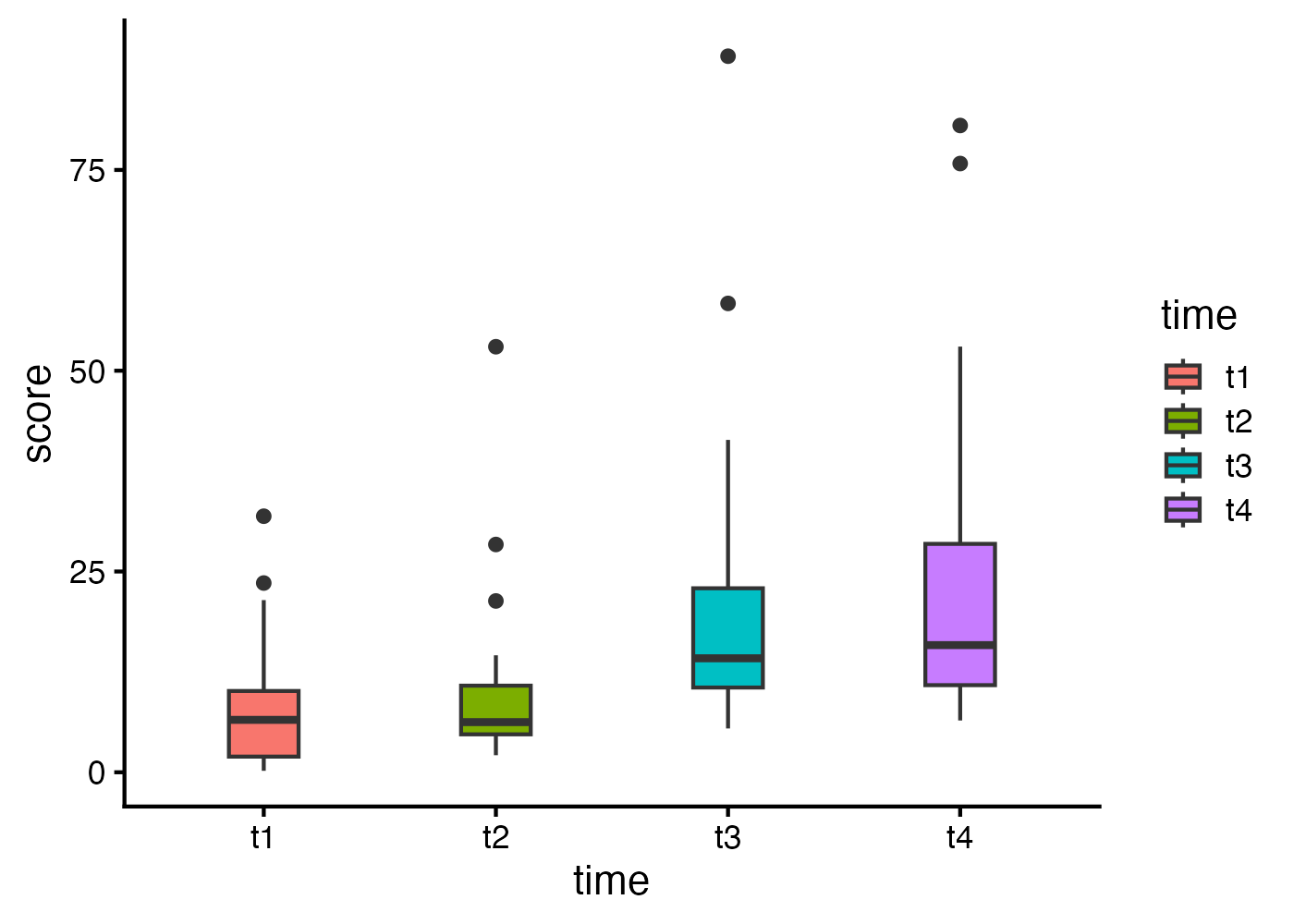


# オムニバス検定
omni = rstatix::friedman_test(dat, score ~ time | id)

# オムニバス検定の効果量（Kendall's W）
# モデル式において、|の後に参加者IDを指定する。
# 信頼区間を計算したい場合は引数に ci = TRUE を加える。
omni_eff = rstatix::friedman_effsize(dat, score ~ time | id)

# 事後検定（対応のあるWilcoxon検定）
post = rstatix::wilcox_test(
  dat, score ~ time, paired = TRUE, p.adjust.method = "holm")

# 事後検定の効果量（rank-biserial correlation）
times = levels(dat$time)
pairs = combn(times, 2, simplify = FALSE)
post_eff = lapply(pairs, function(pair) {
  sub = dat[dat$time %in% pair, ]
  sub$time = factor(sub$time, levels = pair)
  wide = tidyr::pivot_wider(
    sub, id_cols = id, names_from = time, values_from = score)
  eff = effectsize::rank_biserial(
    wide[[pair[1]]], wide[[pair[2]]], paired = TRUE, ci = 0.95)
  data.frame(
    group1 = pair[1], group2 = pair[2],
    r = eff$r_rank_biserial, r_CI_low = eff$CI_low, r_CI_high = eff$CI_high)
})
post_eff = do.call(rbind, post_eff)

# 結果の結合
post_results = base::merge(post, post_eff, by = c("group1", "group2"))

12.7.3 多要因の非パラメトリック：ART

多要因の非パラメトリック分析には、Aligned Rank Transform（ART）を使用します。

多要因の状況で従属変数を単純に順位に置き換えて分散分析を行うと交互作用を正しく調べることができないという問題があります。ARTは主効果や交互作用ごとに他の効果の影響を取り除くことでこの問題を解決した手法です。

12.7.4 2要因（どちらも対応なし）

# データ
dat = data.frame(
  id = factor(1:60),
  A = factor(rep(c("a1", "a2"), each = 30)),
  B = factor(rep(rep(c("b1", "b2", "b3"), each = 10), 2))
)
dat$score = with(
  dat, rexp(60, rate = 0.1) +
    ifelse(A == "a2", 3, 0) +
    ifelse(B == "b2", 3, ifelse(B == "b3", 6, 0)) +
    ifelse(A == "a2" & B == "b1", 3, 0) +
    ifelse(A == "a2" & B == "b2", 10, 0) +
    ifelse(A == "a2" & B == "b3", -2, 0)
)

# 可視化
fig = ggplot(dat, aes(x = A, y = score, fill = B)) +
    geom_boxplot(width = 0.3, position = position_dodge(width = 0.6)) +
    theme_classic(base_size = 16)
plot(fig)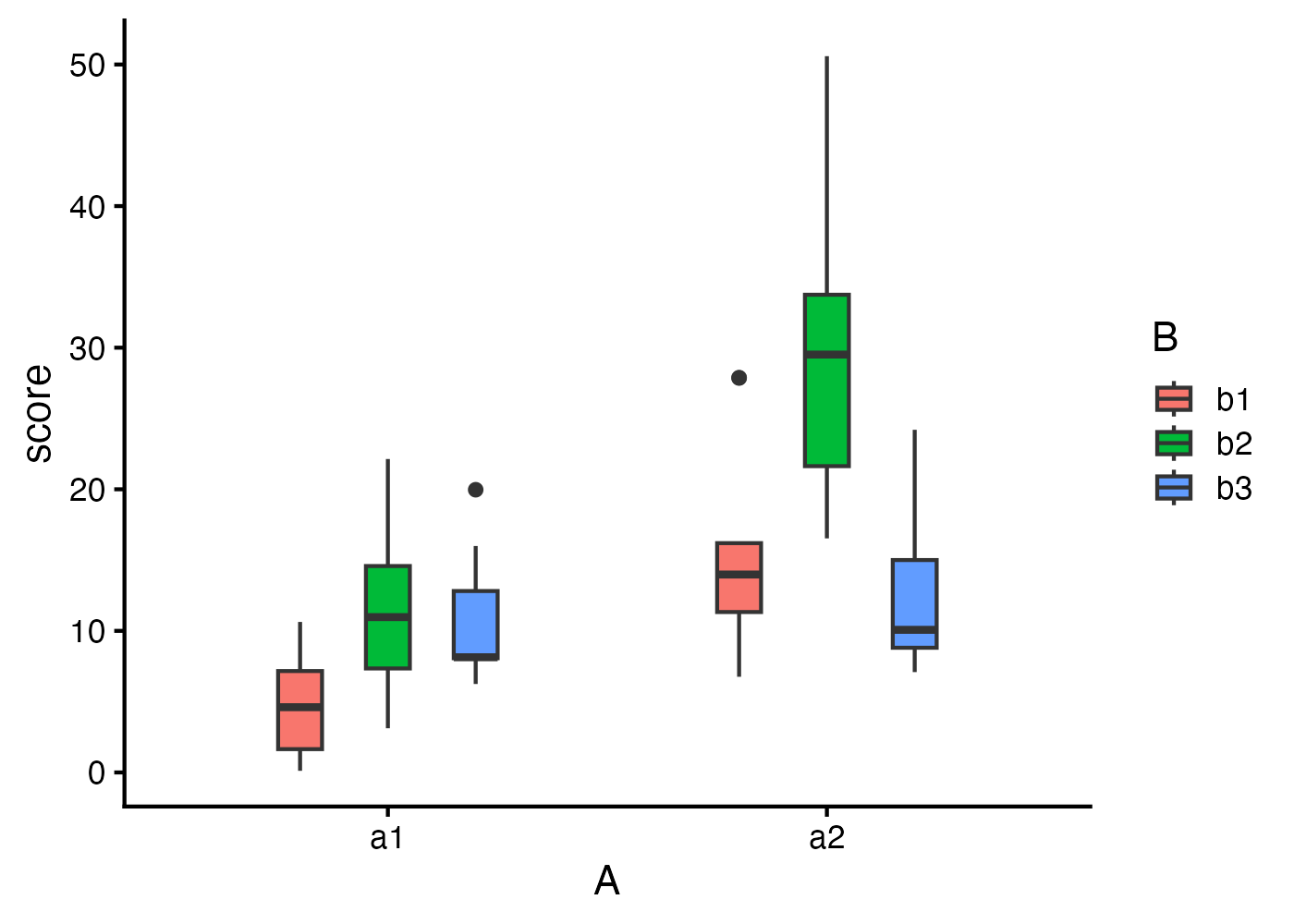


# ARTモデルの適合
art_model = ARTool::art(score ~ A * B, data = dat)

# モデルの妥当性確認（残差の合計が0に近いことを確認）
# Column sumsがすべて0または0に近い値になっていればOK
print(summary(art_model))

# オムニバス検定
omni = stats::anova(art_model)

# オムニバス検定の効果量
omni_eff = effectsize::eta_squared(art_model, partial = TRUE, ci = 0.95)
omni_results = cbind(as.data.frame(omni), as.data.frame(omni_eff))

# 交互作用が有意な場合の単純主効果検定
# 交互作用項のARTモデルからemmeansを取得
art_int = ARTool::artlm(art_model, "A:B")
## Aの各水準におけるBの単純主効果
emm_B = emmeans::emmeans(art_int, ~ B | A)
simple_B = pairs(emm_B, adjust = "holm")
simple_B_summary = summary(simple_B)
simple_B_eff = effectsize::t_to_d(
  t = simple_B_summary$t.ratio,
  df_error = simple_B_summary$df,
  ci = 0.95
)
simple_B_results = cbind(
  as.data.frame(simple_B_summary), as.data.frame(simple_B_eff))
## Bの各水準におけるAの単純主効果
emm_A = emmeans::emmeans(art_int, ~ A | B)
simple_A = pairs(emm_A, adjust = "holm")
simple_A_summary = summary(simple_A)
simple_A_eff = effectsize::t_to_d(
  t = simple_A_summary$t.ratio,
  df_error = simple_A_summary$df,
  ci = 0.95
)
simple_A_results = cbind(
  as.data.frame(simple_A_summary), as.data.frame(simple_A_eff))

# （参考）交互作用が有意でない場合の主効果の事後検定
## Aの主効果
art_A = ARTool::artlm(art_model, "A")
emm_main_A = emmeans::emmeans(art_A, ~ A)
main_A = pairs(emm_main_A, adjust = "holm")
main_A_summary = summary(main_A)
main_A_eff = effectsize::t_to_d(
  t = main_A_summary$t.ratio,
  df_error = main_A_summary$df,
  ci = 0.95
)
main_A_results = cbind(
  as.data.frame(main_A_summary), as.data.frame(main_A_eff))
## Bの主効果
art_B = ARTool::artlm(art_model, "B")
emm_main_B = emmeans::emmeans(art_B, ~ B)
main_B = pairs(emm_main_B, adjust = "holm")
main_B_summary = summary(main_B)
main_B_eff = effectsize::t_to_d(
  t = main_B_summary$t.ratio,
  df_error = main_B_summary$df,
  ci = 0.95
)
main_B_results = cbind(
  as.data.frame(main_B_summary), as.data.frame(main_B_eff))

ARTでは元のデータを整列・順位変換したデータに基づいて検定を行います。したがって、箱ひげ図などで元データをそのまま表示した結果と、ARTの事後検定の結果が不整合であるように見える場合があります（図では差がないように見えるのに検定結果では差があるなど）。

12.7.5 2要因・混合計画（被験者間 × 被験者内）

混合計画をARToolで分析する場合、Error()項を使用して被験者内要因を指定します。

以下のデータではgroupは被験者間要因（control, treatment）、timeは被験者内要因（t1, t2, t3）となるようにデータを生成しています。参加者IDの列を使ってError(id)と指定することで、

# データ
set.seed(101)
n = 15
dat = data.frame(
  id = factor(rep(1:(n*2), each = 3)),
  group = factor(rep(c("control", "treatment"), each = n*3),
                 levels = c("control", "treatment")),
  time = factor(rep(c("t1", "t2", "t3"), times = n*2),
                levels = c("t1", "t2", "t3"))
)
dat$score = with(dat,
  rexp(nrow(dat), rate = 0.1) +
  ifelse(group == "treatment", 2, 0) +
  ifelse(time == "t2", 3, ifelse(time == "t3", 5, 0)) +
  ifelse(group == "treatment" & time == "t3", 9, 0) +
  rep(rnorm(n*2, 0, 2), each = 3)
)

# 可視化
fig = ggplot(dat, aes(x = group, y = score, fill = time)) +
    geom_boxplot(width = 0.3, position = position_dodge(width = 0.6)) +
    theme_classic(base_size = 16)
plot(fig)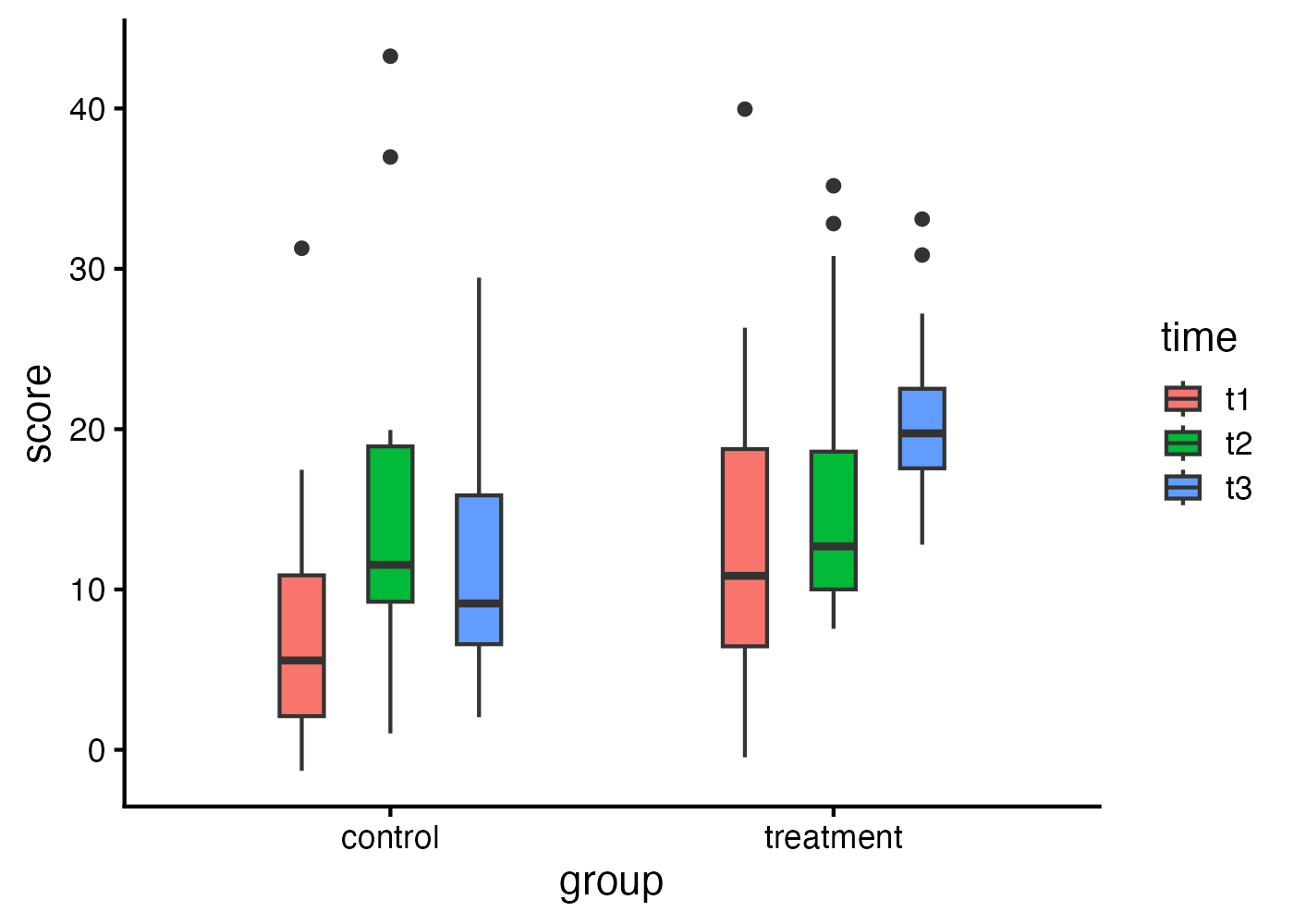


# ARTモデルの適合（Error項で被験者内要因を指定）
art_model = ARTool::art(score ~ group * time + Error(id), data = dat)

# モデルの妥当性確認
print(summary(art_model))

# オムニバス検定
omni = anova(art_model)

# オムニバス検定の効果量
omni_eff = effectsize::eta_squared(art_model, partial = TRUE, ci = 0.95)
omni_results = cbind(as.data.frame(omni), as.data.frame(omni_eff))

# 交互作用が有意な場合の単純主効果検定
art_int = ARTool::artlm(art_model, "group:time")
## groupの各水準におけるtimeの単純主効果
emm_time = emmeans::emmeans(art_int, ~ time | group)
simple_time = pairs(emm_time, adjust = "holm")
simple_time_summary = summary(simple_time)
simple_time_eff = effectsize::t_to_d(
  t = simple_time_summary$t.ratio,
  df_error = simple_time_summary$df,
  ci = 0.95
)
simple_time_results = cbind(
  as.data.frame(simple_time_summary), as.data.frame(simple_time_eff))
## timeの各水準におけるgroupの単純主効果
emm_group = emmeans::emmeans(art_int, ~ group | time)
simple_group = pairs(emm_group, adjust = "holm")
simple_group_summary = summary(simple_group)
simple_group_eff = effectsize::t_to_d(
  t = simple_group_summary$t.ratio,
  df_error = simple_group_summary$df,
  ci = 0.95
)
simple_group_results = cbind(
  as.data.frame(simple_group_summary), as.data.frame(simple_group_eff))

# （参考）交互作用が有意でない場合の主効果の事後検定
## timeの主効果
art_time = ARTool::artlm(art_model, "time")
emm_main_time = emmeans::emmeans(art_time, ~ time)
main_time = pairs(emm_main_time, adjust = "holm")
main_time_summary = summary(main_time)
main_time_eff = effectsize::t_to_d(
  t = main_time_summary$t.ratio,
  df_error = main_time_summary$df,
  ci = 0.95
)
main_time_results = cbind(
  as.data.frame(main_time_summary), as.data.frame(main_time_eff))
## groupの主効果
art_group = ARTool::artlm(art_model, "group")
emm_main_group = emmeans::emmeans(art_group, ~ group)
main_group = pairs(emm_main_group, adjust = "holm")
main_group_summary = summary(main_group)
main_group_eff = effectsize::t_to_d(
  t = main_group_summary$t.ratio,
  df_error = main_group_summary$df,
  ci = 0.95
)
main_group_results = cbind(
  as.data.frame(main_group_summary), as.data.frame(main_group_eff))

12.8 結果の報告

12.8.1 分散分析の結果の報告文

結果の報告文は以下の2つのステップを組み合わせて作成します。

ステップ1：オムニバス検定

1要因の場合：「［要因名］を独立変数とした1要因分散分析の結果、［要因名］の主効果は有意であった（F(2, 27) = 5.30, p = .011, $\eta_p^2$ = .28）。」
2要因の場合：「［要因A］と［要因B］を独立変数とした2要因分散分析の結果、［要因A］の主効果（F(1, 24) = …）は有意であった。［要因B］の主効果は有意ではなかった（F(2, 48) = …）。また、両要因の交互作用は有意であった（F(2, 48) = 6.45, p = .003, $\eta_p^2$ = .21）。」

ステップ2：事後検定

オムニバス検定で有意な差があった場合、具体的にどこに差があったかを続けます。交互作用が有意なときは、まず「単純主効果のF検定」の結果を書き、その後に「ペア比較」の結果を続けます。

交互作用がない場合（主効果とペア比較を記述）：「［要因名］の主効果が有意であったため、Tukey法による多重比較を行った。その結果、［条件1］は［条件2］よりも有意にスコアが高かった（p < .001, d = 0.85）。一方、［条件2］と［条件3］の間には有意な差は認められなかった（p = .120, d = 0.20）。」
交互作用がある場合（単純主効果とペア比較を記述）：「交互作用が有意であったため、単純主効果検定を行った。その結果、［要因Aの水準1］においては［要因B］の単純主効果が認められた（F(2, 48) = 5.10, p = .010, $\eta_p^2$ = .18）。この水準においてTukey法による多重比較を行ったところ、［条件1］は［条件2］よりも有意にスコアが高かった（p = .012, d = 0.60）。」

上記の報告文では、オムニバス検定では統計量にF値、効果量に偏イータ2乗（$\eta_p^2$）を、事後検定のペア比較の効果量としてCohen’s dを記載しています。実際には、用いた分析手法によって異なる効果量が用いられているので、それに合わせて報告文で記載する記号を変える必要があります。

12.8.2 分散分析の統計量の整理

分散分析の手法ごとの統計検定量と効果量をまとめました。

効果量については、このページのスクリプト例で使用したものを記載しているだけであり、他の効果量の指標が用いられる場合もあります。

正規性	要因数	対応の有無	検定名	オムニバス検定の検定量	オムニバス検定の効果量	事後検定の効果量
パラメトリック	1	なし	一元配置分散分析	F	η²_p	d
パラメトリック	1	あり	一元配置反復測定分散分析	F	η²_p	d
パラメトリック	2以上	すべてなし	多元配置分散分析	F	η²_p	d
パラメトリック	2以上	すべてあり	多元配置反復測定分散分析	F	η²_p	d
パラメトリック	2以上	混合	多元配置混合計画分散分析	F	η²_p	d
非パラメトリック	1	なし	クラスカル・ウォリス検定	χ² (H)	η²	r_rb
非パラメトリック	1	あり	フリードマン検定	χ²	W	r_rb
非パラメトリック	2以上	任意	整列ランク変換分散分析（ART）	F	η²_p	d

統計記号の名称一覧

$F$：F値（F-value）
$\chi^2$：カイ二乗値（Chi-square value）
$\chi^2 (H)$：カイ二乗値（H統計量）（Chi-square value (H-statistic)）
$\eta_p^2$：偏イータ二乗（Partial eta-squared）
$\eta^2$：イータ二乗（Eta-squared）
$W$：ケンドールの一致係数（Kendall’s W / Kendall’s coefficient of concordance）
$d$：Cohenのd（Cohen’s d）
$r_{rb}$：順位バイセリアル相関（Rank-biserial correlation）

χ² (H) について：クラスカル・ウォリス検定ではH統計量と呼ばれる統計量が計算されます。これはカイ二乗分布とよく似た分布となるため、H統計量の値をそのままカイ二乗値として報告したり、表記を「χ² (H)」としたりすることが一般的です。