10 Rでt検定
10.1 はじめに
このページではRでt検定を行う方法を解説します。
検定結果(p値など)を算出する方法だけではなく、適切なグラフの作成方法、p値や効果量などの概念の意味、そして仮説検定についてのよくある誤解や解釈の間違いなどについても説明します。
10.1.1 t検定でわかること
t検定は「2つの平均値の間に、偶然とは言えない意味ある差(有意差)があるかどうか」を判定する手法です。
たとえば次のような状況を想像してください:
「全国の大学生の1日の平均勉強時間は60分である」という大規模な調査結果があったとします。あなたは「うちの大学の場合はどうだろうか」と考え、自分の大学の学生20人に勉強時間についてのアンケートを行いました。その結果、その20人の平均勉強時間は75分でした。
さて、この「+15分」の差を見て、「うちの大学の学生は全国平均より勉強熱心だ」と結論づけても良いのでしょうか?
もしかすると、アンケートに答えてくれた20人がたまたま勉強熱心な人が多かっただけ(サンプリングの偏り)かもしれません。その場合、もし別の20人に聞いたら、平均勉強時間は50分になってしまうかもしれません。
- 誤差または偶然:もう一度調査したら結果が変わってしまうかもしれないレベルの差。
- 有意な差がある:何度調査しても「全国平均より高い」という傾向が出ると想定できるレベルの差。
t検定を使うことで、あるグループの平均値と別の平均値の差が、「偶然レベルではなく統計的に意味のある差だと言えるのかどうか」を判定することができます。
10.1.2 3つのt検定の選び方
t検定には大きく分けて3つの種類があり、データの取り方によって使い分ける必要があります。
1. 1つのグループの平均値を基準と比較する:1標本t検定 (One-sample t-test)
- 例:20人分の勉強時間の平均値を全国平均である60分と比較する。
- 「手元のデータ」vs「固定された基準値」の比較です。
2. 異なる対象の比較:対応のないt検定 (Independent samples t-test / Unpaired t-test)
- 例:男子と女子で平均勉強時間に差があるか。
- 例:理系学部と文系学部で英語の平均スコアに差があるか。
- 比較対象が別人である場合など、グループ間に対応関係がない場合の比較です。
3. ペアになる対象の比較:対応のあるt検定 (Paired samples t-test)
- 例:同じ人の「ダイエット前」と「ダイエット後」で体重の差。
- 比較する値が「同じ人」などの基準でペアにできる場合の比較です。
10.1.3 両側検定と片側検定
t検定を行う際、もう一つ決めておかなければならない設定があります。それが「両側検定にするか片側検定にするか」です。
基本は両側検定
t検定を行う際は、特に理由がない限りは両側検定を使用します。
後で紹介するt検定用の関数でも、何も指定しなければデフォルトで両側検定になります。
両側検定 (Two-sided test):
- A群とB群で平均値に差があるかを調べます。
- A群がB群より大きい場合も小さい場合も、どちらも「差がある」とみなします。
- 例:新薬を投与して、数値が「良くなる」か、あるいは副作用で逆に「悪くなる」か、どちらの可能性も考慮して差を検定する場合。
片側検定 (One-sided test):
- 平均値がA群はB群より大きいか(または小さいか)という、特定の方向だけを調べます。
- 逆方向の結果が出た場合は、どんなに差が大きくても「有意差なし」とみなします。
- 例:工場の品質検査で、「不純物の量が基準値より多いこと」だけが問題であり、少ない分には全く関心がない場合。
片側検定は、差をチェックする方向が片側(半分)に絞られるため、有意差が出る基準(ハードル)が両側検定よりも低くなります。つまり、同じデータを分析する場合、片側検定を使う方が有意差が出やすくなります。
ただし、片側検定はそれを使用するべき正当な根拠がある場合にのみ使うようにする必要があります。片側検定の方が有意差が出やすいからという安易な理由で片側検定を使うことはできません。
10.1.4 確認問題:t検定の意義
A組(平均80点)とB組(平均75点)のテスト結果があります。「80点は75点より高いのだから、A組の方が優秀だ」と断定せずに、わざわざt検定を行う理由は何でしょうか?「誤差」という言葉を使って説明してください。
解答と解説(クリックして展開)
その5点の差が、たまたま試験の調子が良かった生徒がA組に多かっただけなどの「偶然の誤差」によって生じたものなのか、それともA組の実力が統計的に見て確実に高いと言える「意味のある差」なのかを区別するため。
10.1.5 確認問題:t検定の選択
ある研究者が、新しい睡眠導入剤の効果を検証したいと考えています。30人の被験者の「薬を飲まない日の睡眠時間」と「薬を飲んだ日の睡眠時間」を測定し、その差を比較することにしました。この場合、選ぶべき検定はどれでしょうか?
- 1標本t検定
- 対応のないt検定
- 対応のあるt検定
解答と解説(クリックして展開)
解答: 3. 対応のあるt検定
同じ被験者(対象)から「服用なし」と「服用あり」の2つのデータを取って比較しているため、睡眠時間データには対応関係(ペアの関係)があります。
10.1.6 確認問題:t検定の選択
あるお菓子メーカーのポテトチップスには「内容量 60g」と表示されています。「本当に60gも入っているのか?」と疑問に思ったあなたは、コンビニでその商品を10袋購入し、中身の重さを計測しました。この10袋の平均重量が、表示されている「60g」と統計的に差があるかを検証するには、どの検定を使うべきでしょうか?
- 1標本t検定
- 対応のないt検定
- 対応のあるt検定
解答と解説(クリックして展開)
解答: 1標本t検定
比較対象が別のグループの平均値ではなく、固定された基準値(60g)であるため、1標本t検定を用います。
10.1.7 確認問題:片側検定
ある統計の初心者が、新薬の効果を検証するために「1標本t検定(両側検定)」を行いましたが、結果は p=0.08 であり、有意差は得られませんでした。
そこで彼は、「薬の効果で数値が下がることはあっても、上がることはあり得ない」と後から考え直し、設定を「片側検定」に変更して再び分析しました。その結果 p=0.04 となり、有意差が示されました。
以上の分析結果に基づいて、彼は「新薬には効果があった」と結論づけました。
この分析者のやり方は、統計学的に見て大きな問題があります。なぜいけないのか、その理由を説明してください。
解答と解説(クリックして展開)
結果を見た後で自分に都合が良いように分析方法や仮説を変更しているから。
- これは「後出しジャンケン」のような不正行為(pハッキング)に該当します。このような行為は第1種の過誤(本当は差がないのに差があるとしてしまう確率)を高めてしまう不当なやり方です。
- データや分析結果を見る前の時点で、片側検定を使用することを確固たる根拠に基づいて事前に決めていたのであれば片側検定の使用は可能ですが、実際にはそのような確たる根拠が持てる場合はそれほど多くないと考えられます。この問題の例でも、「新薬が数値を上げることはあり得ない」と本当に断言できるのか、疑問です。
- 両側検定よりも片側検定の方が有意差が出やすくなりますが、だからといって安易に片側検定を使用することはできません。明確な根拠に基づいて、片側検定を使用することが正当化できる場合にのみ、片側検定を使用します。
10.2 Rによるt検定の実践
10.2.1 分析環境の準備
Rには標準で t.test() というt検定用の関数が用意されています。しかし、このページでは rstatix パッケージの t_test() 関数を使用します。その理由は主に3つあります。
- データフレームで結果が返ってくる:標準の t.test() は結果がリスト形式で返るため、数値の抽出や再利用が少し面倒です。rstatix::t_test() は結果が tibble というデータフレームで返るため、結果をそのままCSVに保存したり、グラフ描画関数に渡したりすることが容易です。
- Tidyverseとの親和性:dplyr や ggplot2 といった現代的なデータ分析ツールと組み合わせて使いやすい設計になっています。
- 構文の統一:t検定だけでなく、分散分析や相関分析なども統一された文法で実行できるため、学習コストが下がります。
Console で以下の命令を実行して rstatix パッケージをインストールしておきましょう。
10.2.2 解析に必要なデータの形(ロング形式)
rstatix や ggplot2 で分析を行うためには、データが「ロング形式」(整然データ)になっている必要があります。もし手持ちのデータがワイド形式の場合は、tidyr::pivot_longer() 関数などを使ってロング形式に変換する必要があります。
ロング形式(整然データ)の詳細や変換方法についてはこちらのページで解説しています。
10.2.3 1標本t検定:基準値との比較
1標本t検定は手元のデータを固定された基準値を比較する場合に使用します。
構文はt_test(データ, 目的変数 ~ 1)となります。
次の例では「あるクラス10名のテストの平均点が、全国平均の50点と異なるか」を検定しています。
library(tidyverse)
library(rstatix)
# サンプルデータ
dat = data.frame(
score = c(45, 52, 57, 49, 54, 55, 51, 48, 52, 53)
)
# 1. 検定の実行
# mu = 50 : 比較したい基準値を指定
res = t_test(dat, score ~ 1, mu = 50)
# 2. 効果量(Cohen's d)と信頼区間の算出
# ci = TRUE を指定することで効果量の95%信頼区間も計算されます
eff = cohens_d(dat, score ~ 1, mu = 50, ci = TRUE)
print(res) # t検定の結果
## # A tibble: 1 × 7
## .y. group1 group2 n statistic df p
## * <chr> <chr> <chr> <int> <dbl> <dbl> <dbl>
## 1 score 1 null model 10 1.43 9 0.186
print(eff) # 効果量の結果
## # A tibble: 1 × 8
## .y. group1 group2 effsize n conf.low conf.high magnitude
## * <chr> <chr> <chr> <dbl> <int> <dbl> <dbl> <ord>
## 1 score 1 null model 0.453 10 -0.17 1.56 smallp値や効果量などが計算されます(これらの値の意味については後ほど説明します)。
結果はデータフレームとして出力されますが、1行しかないので、たとえばp値の値のみを取り出したい時はres$pとすればよいです。
なお、以降の解説では一貫して、有意水準を5%とします(つまり、p値が0.05より小さければ有意な差があったとみなす)。
t_test() 関数について
rstatix::t_test() 関数を使ってt検定を行います。
第一引数に分析対象のデータフレームを指定します。
第二引数には分析のモデル式を指定します。チルダ~の左側にデータの列名を、右側にグループの列名を入れます。1標本t検定の場合はグループ分けがないので右側は1にします。
t_test() 関数の返り値の中身(一部):
- statistic : t値
- df : 自由度
- p : p値
- conf.low/conf.high : 平均値の差の95%信頼区間(信頼区間は、t_test() 関数の引数に
detailed = TRUEを指定すると得られます)
cohens_d() 関数について
rstatix::cohens_d() 関数を使って効果量(Cohen’s d)を計算します。
引数はt_test() 関数と同様です。ci = TRUEを指定することで効果量の95%信頼区間も計算できます。
cohens_d() 関数の返り値の中身(一部):
- effsize : 効果量(Cohen’s d)
- conf.low/conf.high : 効果量の95%信頼区間
結果の記述例
上記の値を使ってt検定の結果を記述します。統計検定量(t値)、自由度、p値のみを報告する最小限のバージョンや、効果量とその信頼区間も報告する詳細バージョンなどの方法があります。
「1標本t検定の結果、有意な差はみられなかった(t(9) = 1.43, p = .19)。」
- 9 は res$df の値であり、自由度です。
- 1.43 は res$statistic の値であり、t値です。
- .19 は res$p の値であり、p値です。
「1標本t検定の結果、有意な差はみられなかった(t(9) = 1.43, p = .19, d = 0.45, 95% CI [-0.17, 1.56])。」
- 効果量(eff$effsize)および効果量の95%信頼区間(下側 eff$conf.low と上側 eff$conf.low)も記載しています。
10.2.4 対応のないt検定
対応のないt検定は異なる2つのグループ(例:A組 vs B組)を比較する場合に使用します。
データの変数には検定したい値に加え、グループを表現する列も含まれている必要があります。
構文はt_test(データ, 目的変数 ~ グループ変数)となります。
# サンプルデータ(A組20名、B組20名)
dat_indep = data.frame(
group = rep(c("Group_A", "Group_B"), each = 20),
score = c(rnorm(20, 70, 8), rnorm(20, 60, 8))
)
res = t_test(dat_indep, score ~ group) # t検定
eff = cohens_d(dat_indep, score ~ group, ci = TRUE) # 効果量なお、rstatix::t_test() は、デフォルトでWelch(ウェルチ)のt検定を行います。これは「2つのグループのばらつき(分散)が等しくなくても使える」方法です。ほとんどの場合このデフォルト設定で問題ありません(もし等分散を仮定する場合は引数でvar.equal = TRUEと指定してください)。
結果の記述例
Welch法を用いた場合、自由度(df)が整数にならず、小数になることがありますが、それは計算上正しい挙動です。そのまま記述して構いません。
「Welchのt検定の結果、両群間に有意な差が認められた(t(37.8) = 3.36, p = .0018)。」
「Welchのt検定の結果、グループAの方がグループBよりも有意にスコアが高かった(t(37.8) = 3.36, p = .0018, d = 1.06, 95% CI [0.44, 1.85])。」
- 単に「群間で差があった」と書くよりも、どちらの群が高かった(低かった)のかを明示する書き方の方がわかりやすくて良いでしょう。
10.2.5 対応のあるt検定
対応のあるt検定は同じ対象の「事前 vs 事後」などを比較する場合に使います。
対応のないt検定と同様に、データにはグループを表現する列も含まれている必要があります。
さらに、グループごとにデータの並び順が同じになっていることが必要です。たとえば、同じ人物の事前と事後のデータの場合であれば、事前と事後で人物の並び順が同じになっている必要があります。下記の例ではPreとPostのどちらの条件でも人物IDが1, 2, 3, …, 20という順番で揃っています。
- ただし、順番さえ同じであれば、IDに該当する列の順番そのものはなんでもいいし、そもそもデータ用の変数にIDに該当する列は含まれていなくても構わない。
構文はt_test(データ, 変数 ~ 条件, paired = TRUE)となります。
paired = TRUE を忘れると対応のないt検定になってしまうので注意してください。
10.2.6 結果の保存
t検定の結果(算出されたさまざまな値)はテキストファイルとして保存しておくと便利でしょう。write.csv() で保存します。
# 検定結果(res)と効果量(eff)を結合して保存する例
final_result = bind_cols(
dplyr::select(res, c(df, statistic, p)),
dplyr::select(eff, c(effsize, conf.low, conf.high))
)
write.csv(final_result, "t-test.csv", quote = FALSE, row.names = FALSE)dplyr::select() 関数で保存したい列のみを抽出し、bind_cols() 関数でデータフレームを横方向に結合しています。
10.2.7 確認問題:t検定の結果の報告
あるデータのA群とB群のスコアを比較するために以下のコードを実行しました。
# 対応のないt検定(Welchのt検定)
res = t_test(dat, score ~ group)
# 効果量(信頼区間あり)
eff = cohens_d(dat, score ~ group, ci = TRUE)出力結果(一部)
- res$statistic: 2.45
- res$df: 15.3
- res$p: 0.027
- eff$effsize: 1.12
- eff$conf.low: 0.15
- eff$conf.high: 2.09
これに基づいて、t検定の結果を報告する文を作成してください。
解答と解説(クリックして展開)
解答例:
- A群とB群の間に有意な差がみられた (t(15.3) = 2.45, p = .027)。
- A群とB群の間に有意な差がみられた (t(15.3) = 2.45, p = .027, d = 1.12, 95 %CI [0.15, 2.09])。
なお、t, p, d などの統計概念の記号は斜体(イタリック体)にする必要があります。
10.3 データの可視化
t検定に限らずですが、単に検定を実施してp値を確認することだけが分析なのではありません。データを可視化することも重要です。
なぜ図を描く必要があるのでしょうか? 主な理由は2つあります。
1. データの入力ミスなどによる異常値に気づくため
- 例えば身長のデータで、170 と打つべきところを 1700 とタイプミスしていたとします。平均値だけを見ていると値が少し高くなるだけなのでミスに気づきませんが、図に描けば「異常な点」としてすぐに発見できます。
2. データの分布形状を確認するため
- t検定は「データがある程度、正規分布(左右対称な山型の分布)していること」を前提としています。分布が極端に歪んでいないかを図によって確認できます。
10.3.1 論文掲載用グラフの作成
ここからは、論文に使える質の高いグラフの書き方を紹介します。
よく見かける「エラーバー付きの棒グラフ」は、データの分布の情報を隠してしまうため、近年はあまり推奨されなくなっています。
ここでは、「平均値」+「ばらつき(エラーバー)」+「生のデータ点(ジッター)」をすべて見せる、現代的なグラフの作成方法を学びましょう。
データの準備
サンプルデータを作成します。「2つのグループ(A群、B群)のテストスコア」を想定しています。
library(tidyverse)
set.seed(123) # 乱数を固定(毎回同じデータを生成するため)
# サンプルデータの作成(datという変数に入れます)
# group: グループ
# score: テストの点数
dat = data.frame(
group = rep(c("Group_A", "Group_B"), each = 20),
score = c(rnorm(20, mean = 60, sd = 10), rnorm(20, mean = 70, sd = 10))
)
# データの確認(ロング形式になっています)
print(head(dat))
## group score
## 1 Group_A 54.39524
## 2 Group_A 57.69823
## 3 Group_A 75.58708
## 4 Group_A 60.70508
## 5 Group_A 61.29288
## 6 Group_A 77.15065平均値プロット
平均値を「点」で示し、その信頼性(標準誤差など)を「エラーバー」で示します。さらに背景に「生のデータ」を散らすことで、データの全貌をそのまま伝えます。
平均値の比較という状況では、エラーバーとして標準誤差(SE)や95%信頼区間(95% CI)が使われます。下記の例ではfun.data = "mean_se"と指定して標準誤差のエラーバーを作成しています。
# 平均値プロットの作成
fig_mean = ggplot(dat, aes(x = group, y = score, color = group)) +
geom_jitter(width = 0.03, alpha = 0.4, size = 2, color = "black") +
stat_summary(fun.data = "mean_se", geom = "errorbar", width = 0.1, linewidth = 1.5) +
stat_summary(fun = "mean", geom = "point", size = 5) +
labs(y = "Test Score", x = "Group", caption = "エラーバーは標準誤差を表す") +
theme_classic(base_size = 20) +
theme(
legend.position = "none", # 凡例を非表示にする
plot.caption = element_text(hjust = 0) # キャプションを左寄せにする
)
# グラフの表示
print(fig_mean)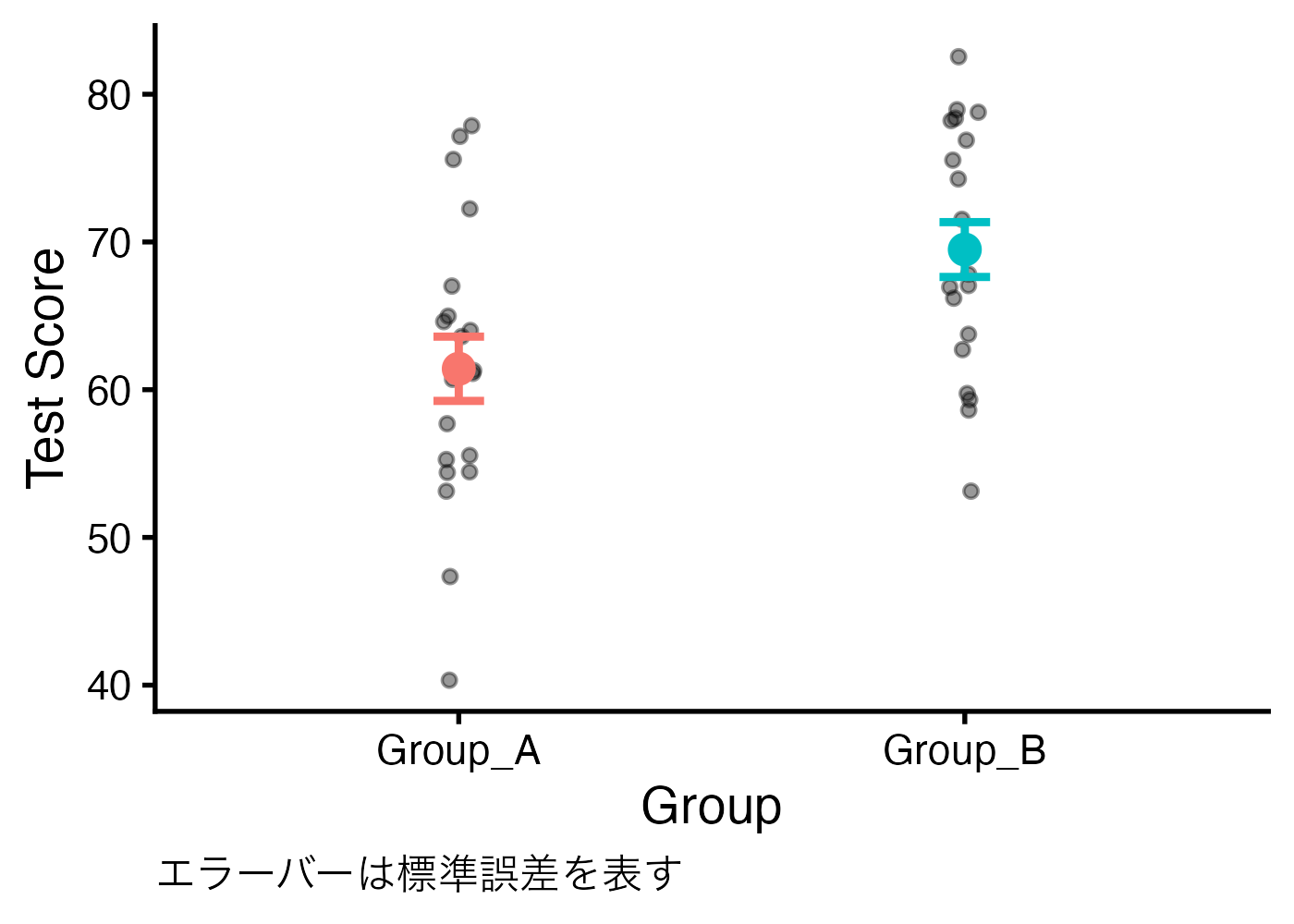
図のキャプションには必ず「エラーバーは標準誤差を表す」などのようにエラーバーの種類を明記する必要があります。上の例では ggplot の機能を使ってそのようなキャプションを加えましたが、実際には図のキャプションはWordなど文書作成ソフト上で追加することが多いと思われます。
なお、エラーバーに95%CIを使いたい場合はfun.data = "mean_cl_normal"と指定します。ただし、"mean_cl_normal" を使うためには Hmisc パッケージが必要です。 install.packages("Hmisc")でインストールし、library(Hmisc)で有効化しておく必要があります。
[発展]グラフへの検定結果の挿入
検定結果(有意差があるかどうか)をコの字型の線(ブラケット)や*記号を用いて図に記入することがあります。ggpubr パッケージを使うことでそうした要素をggplot2 の図に追加することができます。
グラフに線を引くためには、p値だけでなく、「どの高さに、どのグループ間に線を引くか」という座標情報(x, y)が必要です。 rstatix::add_xy_position() 関数がそれを計算してくれます。
その結果を使い、ggpubr::stat_pvalue_manual() 関数を ggplot のレイヤーとして追加します。
# 未インストールの場合は install.packages("ggpubr") を実行
library(tidyverse)
library(rstatix)
library(ggpubr)
# 前項と同じサンプルデータを使用
dat = data.frame(
group = rep(c("Group_A", "Group_B"), each = 20),
score = c(rnorm(20, mean = 60, sd = 10), rnorm(20, mean = 70, sd = 10))
)
# t検定を行い、グラフ上の表示位置(xy座標)を計算する
# t_test()の結果を格納した変数に座標情報を追加しています
stat_test = t_test(dat, score ~ group) %>%
add_significance() %>%
add_xy_position(x = "group")
# 平均値プロットの作成
fig_mean = ggplot(dat, aes(x = group, y = score, color = group)) +
geom_jitter(width = 0.03, alpha = 0.4, size = 2, color = "black") +
stat_summary(fun.data = "mean_se", geom = "errorbar", width = 0.1, linewidth = 1.5) +
stat_summary(fun = "mean", geom = "point", size = 5) +
stat_pvalue_manual(
stat_test, label = "p.signif",
size = 10, bracket.size = 0.8, bracket.nudge.y = 5) +
labs(y = "Test Score", x = "Group", caption = "エラーバーは標準誤差を表す") +
theme_classic(base_size = 20) +
theme(
legend.position = "none", # 凡例を非表示にする
plot.caption = element_text(hjust = 0) # キャプションを左寄せにする
)
# グラフの表示
print(fig_mean)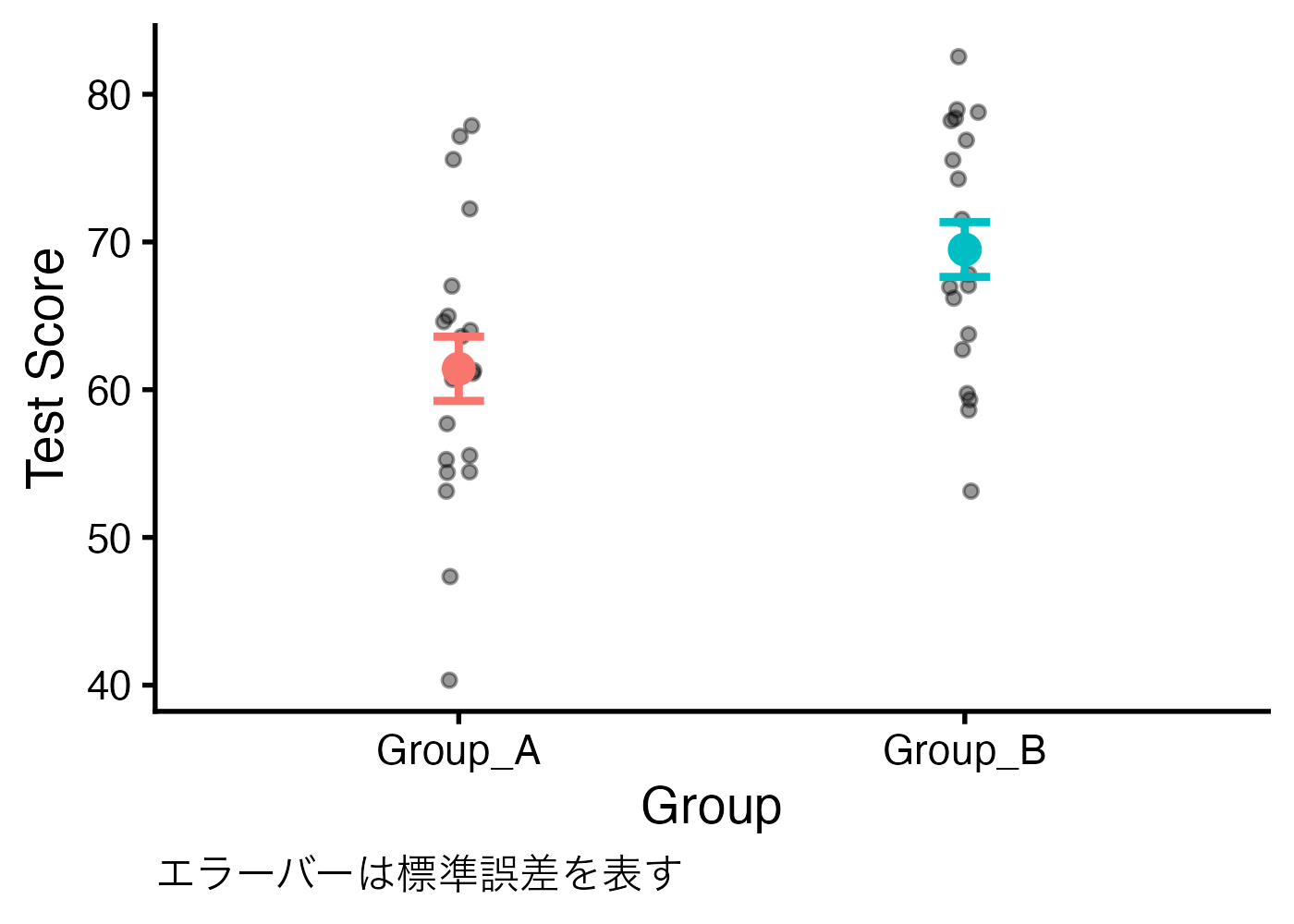
平均値プロットの作成の箇所は、stat_pvalue_manual() 関数が追加された以外は前項と同じです。stat_pvalue_manual() 関数にはさまざまな引数があり、グラフの見た目を調整できます。詳しくは関数のヘルプを参照してください(Console で?stat_pvalue_manualを実行する)。
箱ひげ図
分布の形や四分位範囲をしっかり見せたい場合は、箱ひげ図(Boxplot)が適しています。この場合も、生のデータ点(ジッター)を重ねるのが親切です。
fig_box = ggplot(dat, aes(x = group, y = score, fill = group)) +
geom_boxplot(width = 0.1, alpha = 0.7, outlier.shape = NA) +
geom_jitter(width = 0.2, alpha = 0.4) +
labs(y = "Test Score", x = "Group") +
theme_classic(base_size = 20) +
theme(legend.position = "none")
print(fig_box)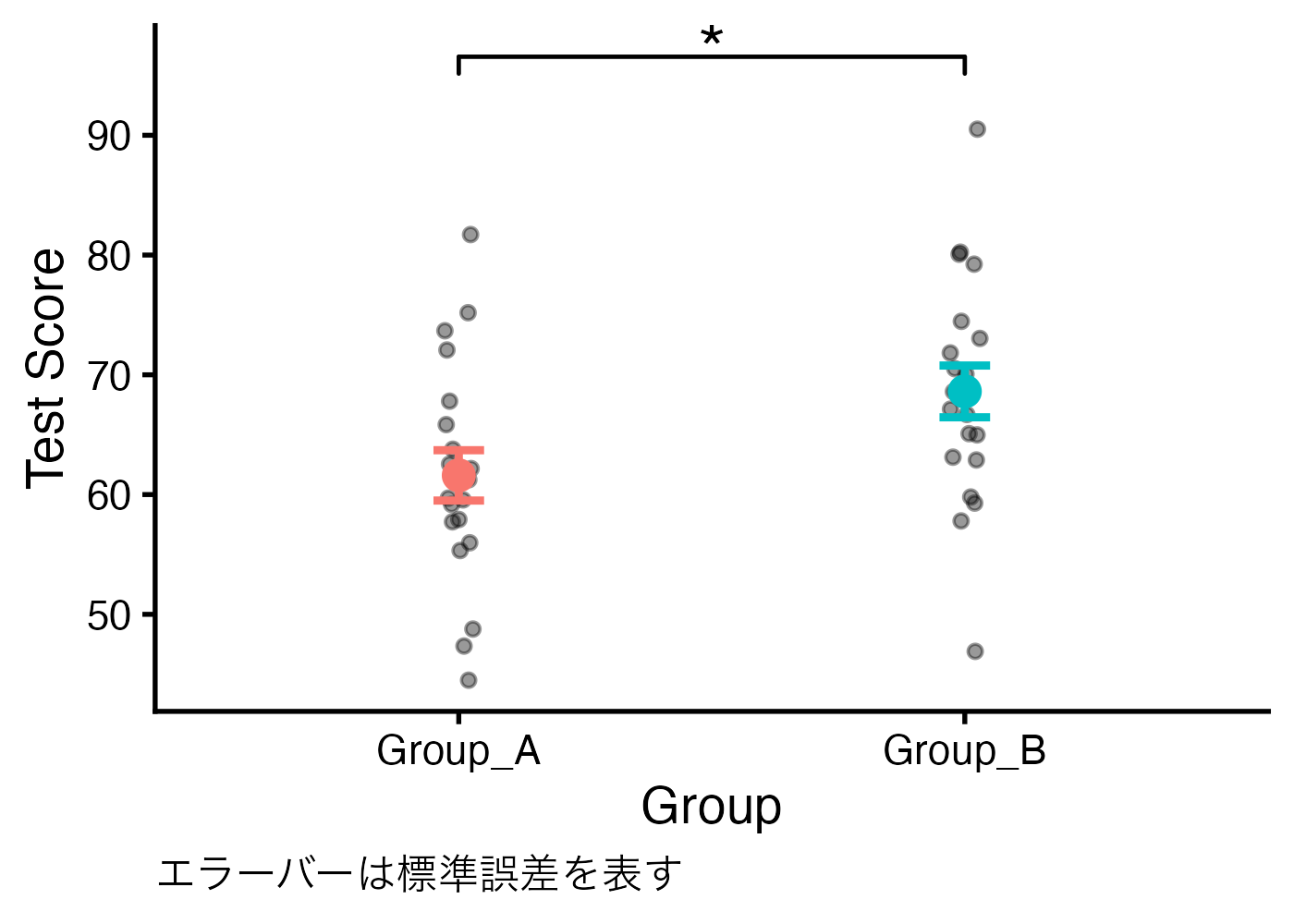
10.3.2 確認問題:棒グラフ
上記のデータ(dat)を使い、「エラーバー付きの棒グラフ」に生データを表示させた図を作成してください。ただし、エラーバーには 95% CI を使ってください。
解答と解説(クリックして展開)
library(Hmisc)
fig_bar = ggplot(dat, aes(x = group, y = score, fill = group)) +
stat_summary(fun = "mean", geom = "bar", width = 0.25) +
stat_summary(fun.data = "mean_cl_normal", geom = "errorbar", width = 0.1, linewidth = 1.5) +
geom_jitter(width = 0.1, alpha = 0.4, size = 2, color = "black") +
labs(y = "Test Score", x = "Group", caption = "エラーバーは95% CIを表す") +
theme_classic(base_size = 20) +
theme(
legend.position = "none", # 凡例を非表示にする
plot.caption = element_text(hjust = 0) # キャプションを左寄せにする
)
print(fig_bar)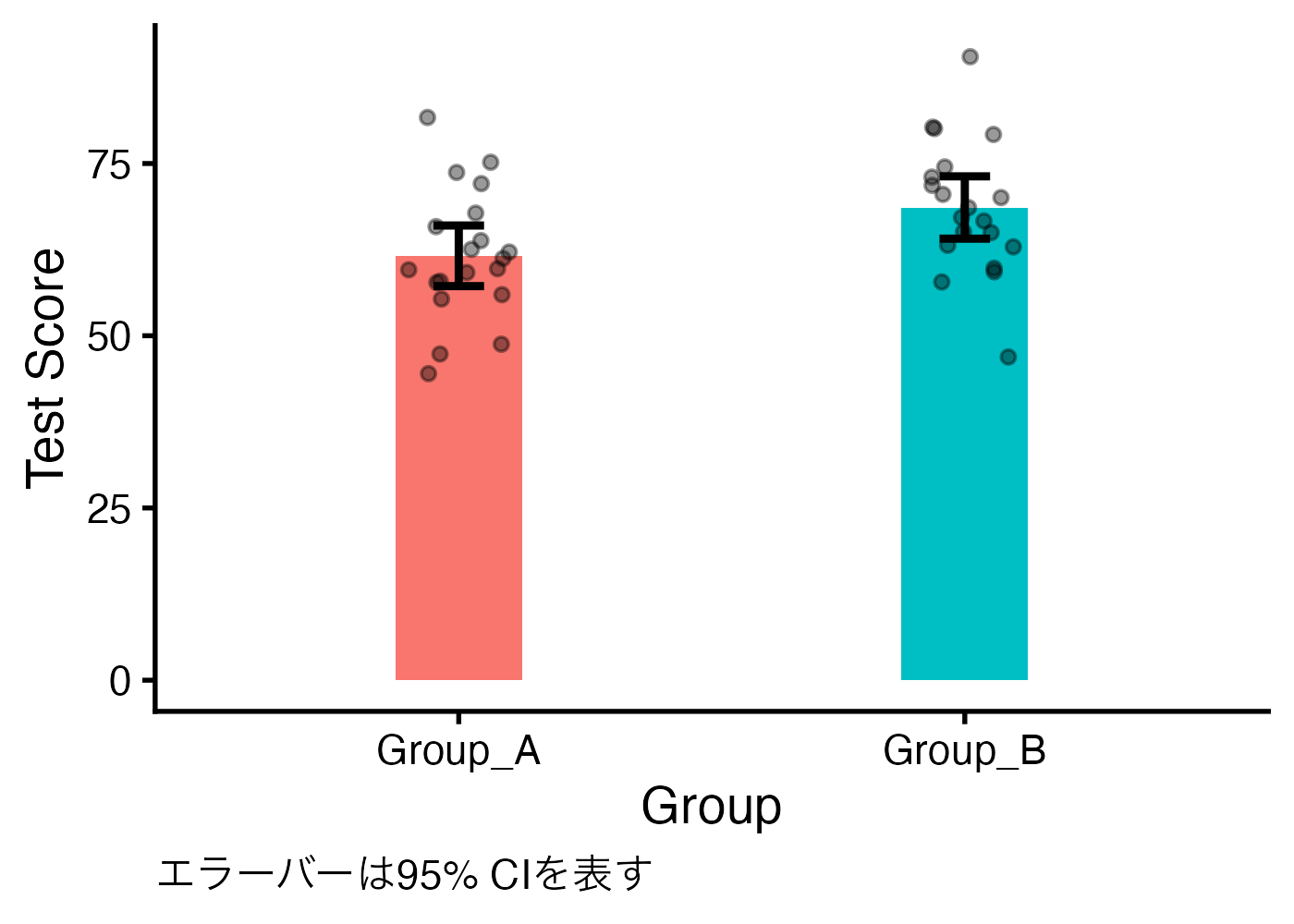
- 棒グラフの場合は棒の手前に生データ点を表示させると見やすいので、棒、エラーバー、ジッターの順で描画するようにしています。
- この解答例ではエラーバーと生データ点がどちらも黒色なので見分けにくく、改善の余地があるかもしれません。
10.4 結果の解釈とよくある誤解
Rを使えばp値や効果量などの値を計算することは簡単にできます。しかし、その数字が何を意味するのかを理解しておかないと、分析結果の解釈を誤ってしまいます。
ここでは、統計検定の結果を解釈する上で知っておくべき事項と、初心者が陥りがちな誤解について解説します。
10.4.1 p値(p-value)
p値は「0.05(5%)未満なら有意差あり」という基準で使われることが多いですが、それはどういう意味でしょうか。
そもそもp値とは、「もし本当は差がない(帰無仮説が正しい)のだとしたら、今回得られたデータのような(あるいはそれよりもっと極端な)差が偶然に生じる確率はどれくらいか?」 という確率のことです。
検定のプロセスを裁判に例えるとわかりやすいでしょう。
- 前提(帰無仮説):「被告人は無実(平均値に差はない)である」と仮定する。
- 証拠(データ):検察官が「データからこんなに怪しい証拠(大きそうな平均値の差)が出ました!」と提示する。
- 判断(p値):裁判官は考えます。「無実の人から、このような大きさの差(証拠)が偶然によって生じる確率はどれくらいだろうか?」
- 確率(p値)が高い(例:p = 0.30, 30%) → 「これくらいの差であれば偶然でもそれなりの確率で生じることがある。これだけでは有罪(差がある)とはみなせない(帰無仮説を棄却できない)。」
- 確率(p値)が極めて低い(例:p = 0.01, 1%) → 「無実の人からこれほどの差が生じることはめったに起こり得ない。ということは、無実という前提が間違っているということだ。したがって、帰無仮説を棄却し、有罪(差がある)と認めよう。」
この「めったに起こり得ない」のライン(=有意水準)として、慣習的に5%が使われています。したがって、p値が0.05未満であった場合に、有意差があるとみなすのです(今回のデータで得られた平均値の差がただの偶然で生じる確率は5%よりも小さいので、その差は偶然ではなく、統計的に確かな差があるのだ、と判定する)。
10.4.2 効果量(Cohen’s d)
p値には、「サンプルサイズ(データの件数)が大きいと、非常に小さな差でもp値は小さくなる(つまり有意になる)」という性質があります。たとえば、数十万人規模のデータを分析すれば、「グループ間の試験の平均点が0.01点違う」だけでも有意差あり(p < 0.05)という結果が出ます。しかし、たとえ「有意差あり」という結果が得られたとしても、たった0.01点の差に現実的な意味はあるでしょうか?
そこで重要になるのが効果量(Effect Size)です。これはサンプルサイズに依存しない、純粋な「差の大きさ」を表す指標です。効果量はその名の通り、その値が大きいほど効果(差)が大きいということを意味します。
効果量にはいくつかの指標がありますが、t検定の場合はCohen’s dという指標がよく使われます。Cohen’s dの大きさの解釈として以下の基準がよく紹介されています。
- 0.2 : 小さい効果(Small)
- 0.5 : 中程度の効果(Medium)
- 0.8 : 大きい効果(Large)
しかし、この基準は実際にはあまり役には立ちません。どのくらいの効果量であれば大きい(あるいは意味のある)効果だと言えるのかは、分析対象次第だからです。
たとえば、あるアプリのボタンのデザインを変えることで、ユーザーの滞在時間がわずかに(d = 0.1)伸びるだけであったとしても、利用者が数億人もいるプラットフォームであれば、その小さな差の積み重ねが企業に数百億円もの利益をもたらすことがあり得ます。あるいは、人間の心理現象などのように不確定要素の多い分野では、d = 0.2ほどの効果量であっても、心理メカニズムを解明する重要な手がかりだとみなされます。
したがって、効果量の値を解釈する際は安易に定番の基準(0.2なら小さな効果、0.5なら中程度、0.8なら大きな効果)を当てはめないようにしましょう。その分野でどのくらいの効果量が典型的に報告されているかや、その効果の大きさが実質的にどのような意味を持つのかを考えて、効果量の値を解釈する必要があります。
10.4.3 95%信頼区間(95% CI)
95%信頼区間(CI: Confidence Interval)は、推定の幅(不確実性)を表します。
信頼区間の意味:
× 「推定対象の真の値が95%の確率でこの区間に入る」
◯「同様の観測(実験や調査)を100回行ったら、そのうち95回は算出された区間の幅の中に真の値が含まれるだろう」
少しややこしいですが、実用的には「推定結果のブレ幅」と捉えてください。
- 区間が狭い: 推定の精度が高い(データ数が多い、ばらつきが小さい)。
- 区間が広い: 推定の精度が低い。結論を急ぐにはデータ不足かもしれない。
10.4.4 初心者が陥りやすい誤解
誤解①:「p値がすごく小さいから、効果(差)もすごく大きい」
- 間違いです。「p = 0.00001」は、「差があることの確信度が高い」ことを示しているだけで、「差が巨大である」こと意味しません。効果量はごくわずか(d = 0.1など)かもしれません。効果が大きいかどうかはp値ではなく効果量を調べる必要があります。
誤解②:「有意差が出なかった(p>0.05)= 差がないことが証明された」
- 間違いです。それは「差があるとは言えなかった(証拠不十分)」だけであり、「差がない(同じである)」ことを支持する証拠にはなりません。
- そもそも、t検定を使う限り、差がないということを主張することはできません。もし「差がない」ということを積極的に主張したい場合は、「同等性検定(Equivalence test)」などの、他の統計手法を使う必要があります。
誤解③:「95%信頼区間が重なっていなければ、有意差ありだ」
- 半分正解ですが、不正確です。2つのグループのエラーバー(95% CI)が重なっていなければ、通常は p<0.05 になります。しかし、「少し重なっていても有意差が出る(p<0.05)」ケースはよくあります。 グラフの見た目(重なり)だけで有意差を判定せず、p値を確認するようにしてください。
10.4.5 確認問題:非有意な結果の解釈
A群とB群の比較を行ったところ、p = 0.12 という結果になりました。レポートの結論として不適切(誤り)な記述はどれですか?
- 「A群とB群の間に、統計的に有意な差は認められなかった。」
- 「A群とB群に差があるという証拠は得られなかった。」
- 「A群とB群の成績は同等の水準であることが示された。」
- 「有意水準5%において帰無仮説を棄却できなかった。」
解答と解説(クリックして展開)
解答: 3. 「A群とB群の成績は同等の水準であることが示された。」
p値が有意水準(0.05など)を超えている場合、「差があるとは言えない」だけであり、「差がない」ことを示したことにはなりません。
10.4.6 確認問題:効果量の大きさの解釈
ある研究で、「SNS上で見かける他人からの投稿からポジティブな単語が少なくなった場合、その人自身がSNS上でネガティブな単語を使う割合が0.04%増えた」という結果が報告されました(p = 0.007, Cohen’s d = 0.001)。この結果は、「SNS上ではユーザー同士の間で感情の伝染が起こっている」ことを示していると、この研究を行った研究者たちは結論づけました。
p値や効果量の値の大きさから考えて、この研究者らの主張は妥当と言えるか論じてください。
解答と解説(クリックして展開)
p値は0.05を下回っており、有意な結果ではあると言えます(SNSでポジティブ単語をあまり見なかった人はネガティブ単語を使う割合が統計的に有意に増える)。
一方で、その効果は非常に小さいと言えます。ネガティブな単語を使う割合が増えるといっても、具体的にはたったの0.04%(4%ではなく、0.04%)しか増えていません。効果量dは0.001という非常に小さな値です。
この研究は2014年にFacebook社から報告されたものです。
Kramer, A. D., Guillory, J. E., & Hancock, J. T. (2014). Experimental evidence of massive-scale emotional contagion through social networks. Proceedings of the National Academy of Sciences, 111(24), 8788-8790.
https://www.pnas.org/doi/10.1073/pnas.1320040111
この研究の著者らは、効果量が小さいことは認めつつも、この小さな効果量には重大な意味があると主張しています。なぜなら、Facebookのような巨大プラットフォームにおいては、個人ごとの変化が微小でも、全体への影響は甚大になるからです。d = 0.001 という小さな効果であっても、Facebookの規模(実験当時の2013年初頭)で換算すると、「1日に数十万件もの感情的な投稿がSNS上で増減する」ことに相当します。感情の状態は心身の健康(well-being)と関連しているため、これほど大規模な感情の変化は公衆衛生レベルで無視できない影響を持ちうる、と著者らは論じています。
[解説]この論文の著者らの主張がどこまで妥当かは議論の余地があります。ともあれ、効果量の値そのものが極めて小さい場合でも、そこからただちに「小さな効果である(だからあまり意味はない)」という結論を導くことはできない、ということは意識しておく必要があります。
10.5 [発展]データが不適切な場合の対処
t検定は、データ(の背景にある確率分布)が正規分布に従っていることを前提としています。この前提が満たされているかを確認するために、分析対象の各グループの測定値の分布が左右対称の山型になっているかをヒストグラムを描くなどしてチェックします。
この前提条件(正規性の仮定)が満たされていればt検定を使うことができますが、そうでない場合(分布が歪んでいる場合など)はt検定の使用が問題になることがあります。特に、サンプルサイズ(データの件数)が少ない場合には、別の分析方法を採用することを検討すべきかもしれません。
10.6 発展的問題
10.6.1 p値と効果量
サンプルサイズが検定結果に与える影響を理解するために、極端な2つのケース(実験A、実験B)を比較します。 以下のコードでデータを生成してください。
set.seed(123)
# 実験Aのデータ(n = 1000)
datA = data.frame(
group = rep(c("Pre", "Post"), each = 1000),
score = c(rnorm(1000, 50, 15), rnorm(1000, 51, 15))
)
# 実験Bのデータ(n = 10)
datB = data.frame(
group = rep(c("Pre", "Post"), each = 10),
score = c(rnorm(10, 50, 12), rnorm(10, 58, 12))
)問題
- 実験AとBについて、t検定の結果(p値)と効果量(Cohen’s d)を計算してください。
- 実験Aは有意差あり(p < 0.05)、実験Bは有意差なし(p > 0.05)」という結果になります。有意差が出た実験Aの方が成功だと考えられがちですが、効果量の観点から、実験Bの方が(将来的には)有望かもしれないと言える理由を論じてください。
解答と解説(クリックして展開)
# t検定と効果量を計算する
resA = t_test(datA, score ~ group)
effA = cohens_d(datA, score ~ group, ci = TRUE)
print(paste0("Exp. A: p = ", resA$p, ", d = ", abs(effA$effsize)))
## [1] "Exp. A: p = 0.0378, d = 0.0929366790266166"
resB = t_test(datB, score ~ group)
effB = cohens_d(datB, score ~ group, ci = TRUE)
print(paste0("Exp. B: p = ", resB$p, ", d = ", abs(effB$effsize)))
## [1] "Exp. B: p = 0.0676, d = 0.875265995164827"
- 実験Aは有意差はあるものの、効果量は0.1未満と小さくなっています。
- 実験Bは有意差はありませんが、それはサンプルサイズ不足で推定精度が低いからです。もしデータ件数の大きな実験を行っていれば、実験Bは有意差があり、かつ大きな効果量を持つという結果になった可能性があります。
- [補足]ただし、サンプルサイズが小さい場合、計算された効果量の値もあまり信頼ができないので、実際に実験Bを大きなサンプルサイズで実験した場合には効果量が今回の結果よりもかなり低くなることは十分にあり得る(今回の結果で、効果量の95%信頼区間が広いということに対応します)ので注意が必要です。
- [補足]なお、効果量の値が負である場合は絶対値で報告して構わないし、その方がわかりやすいでしょう。効果量の値が正か負かは平均値の引き算をする際にどちらの条件を基準にしているかだけの問題です(Pre引くPostか、Post引くPreか)。したがって、正か負かは関係なく、値の絶対値が大きければ効果量は大きく、0に近いほど効果量は小さいことを意味します。