11 Rで相関分析
11.1 相関分析について
「風が吹けば桶屋が儲かる」ということわざがありますが、データ分析の世界でも「ある数値が変わると、別の数値も連動して変わるかどうか」を知りたい場面がよくあります。
たとえば、
- 気温が高い日ほど、アイスクリームがよく売れるのではないか?
- 勉強時間が長い学生ほど、テストの点数が高いのではないか?
- スマホの使用時間が長いほど、視力は下がるのではないか?
といったように、2つの変数の間にあるであろう関連性(相関関係)を分析する際に、相関分析を用いることができます。
11.1.1 相関の向き(正負)と強さ
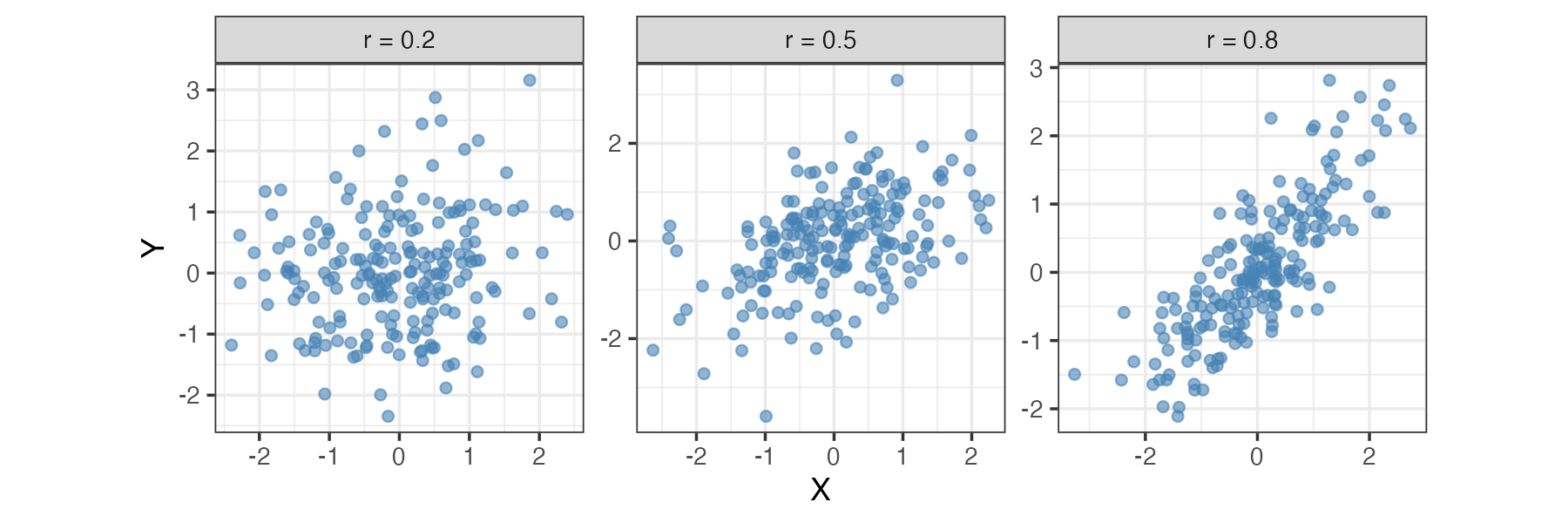
相関係数(correlation coefficient)は、通常 -1 から +1 の間の値をとります。
- 正の相関 (r > 0): 片方が増えると、もう片方も増える関係(例:身長と体重)。
- 負の相関 (r < 0): 片方が増えると、もう片方は減る関係(例:寒さとアイスの売上)。
- 相関が無いまたは弱い (r ≈ 0): 2つの変数に関連が見られない状態。
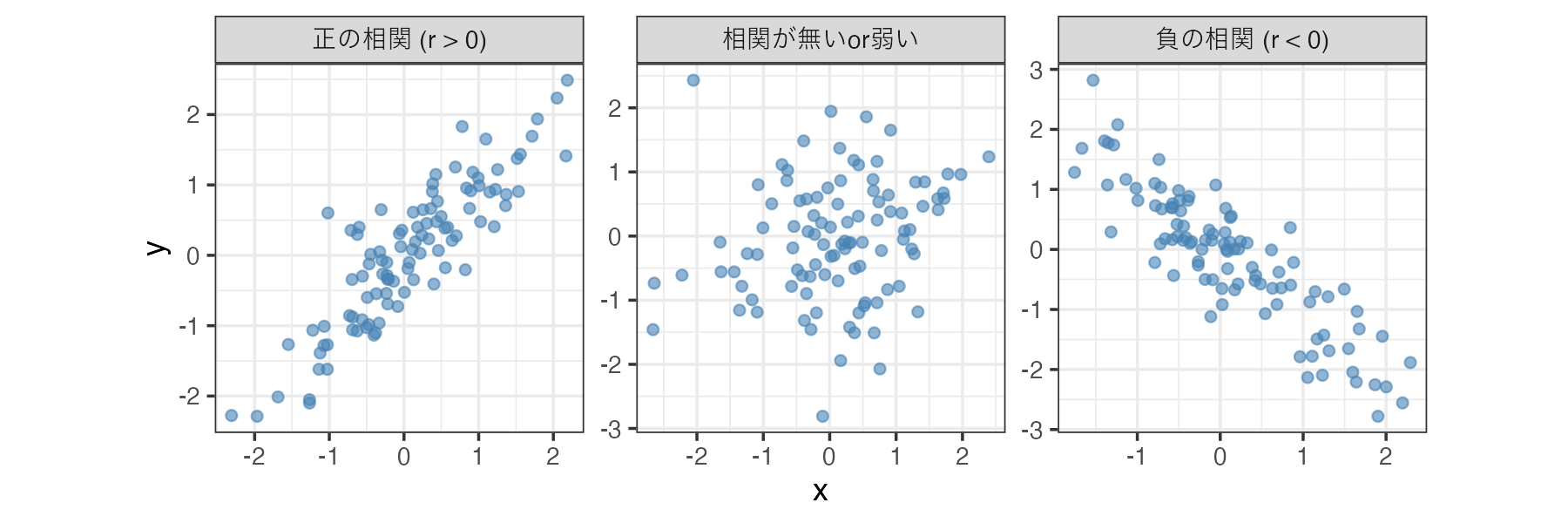
相関係数はその値(の絶対値)が大きいほど変数間の関連が強いことを意味します。
11.1.2 相関係数の種類
相関係数にはいくつかの種類があり、データの性質に応じて使い分ける必要があります。
ピアソンの積率相関係数(Pearson’s r)
最も一般的で、標準的な手法です。単に「相関係数」といった場合、通常はこれを指します。「ピアソンの相関係数」や「ピアソンのr」などとも呼ばれます。
ピアソンの相関係数使える条件:
- データが「間隔尺度」または「比率尺度」である(身長や試験の点数など)。
- データが「正規分布」に従っている(釣鐘型の分布)。
- 2変数の関係が「直線的」である。
ピアソンのrは外れ値の影響を受けやすいので、データに極端な値がある場合やサンプルサイズが小さい場合、計算された相関係数の値は信頼できない可能性があります。
順位相関係数
順位データ(順序尺度)の場合や、データが正規分布していない、あるいは外れ値が含まれている場合には、順位相関係数を使います。データの数値をそのまま使わず、順位に変換して計算する手法です。
順位相関係数にはいくつか種類があり、よく使われるのは以下の2つです。
- スピアマンの順位相関係数(Spearman’s ρ)
- ケンドールの順位相関係数(Kendall’s τ)
基本的にはスピアマンを使えばよいですが、サンプルサイズが小さかったり(N<20∼30)、データに同じ順位の回答が多かったりする場合(5段階評価で3の回答が多いなど)には、ケンドールの順位相関係数の方がより正確に相関を推定できるため推奨されます。
なお、相関係数の記号にピアソンは r、スピアマンは ρ(ロー)、ケンドールは τ(タウ)が使われます。
ピアソンの相関係数とスピアマンの相関係数の2つは使う機会が多く、そして適切に使い分ける必要があるので、それぞれの名前を覚えておくようにしましょう。ピアソンとスピアマンは名前がちょっと似ているので、どっちがどっちだったか混乱しやすいです。文字数の短いピアソンが基本的な方の相関係数で、文字数の長い方のスピアマンがややこしい方の相関係数(順位相関)だと覚えておけばいいと思います。
11.1.3 分析の準備
Rには相関分析のための関数として cor() や cor.test() などが標準で用意されていますが、出力結果が見づらいなど、不便さもあります。
このページでは、Rの標準機能に加えて、以下の便利なパッケージを使用します。
- correlation パッケージ:相関分析の結果を dplyr で扱いやすい「整然データ(Tidy data)」として出力してくれます。
- ggpubr パッケージ:ggplot2 を拡張したもので、論文にそのまま掲載できる高品質のグラフを作成できます。
11.1.4 確認問題:相関係数の理解
ある研究で「スマートフォンの1日あたりの使用時間」と「その日の睡眠時間」の関係を調査しました。その結果、相関係数は r = −0.3 でした。この結果の解釈として最も適切なものはどれでしょうか?
- スマホを長く使う人ほど睡眠時間は長くなる傾向がある。
- スマホを長く使う人ほど睡眠時間は短くなる傾向がある。
- 相関係数がマイナスなので計算間違いである可能性が高い。
- スマホの使用時間が原因で睡眠時間が短くなっている。
解答と解説を表示
解答: 2
解説:
- 1は誤り。これは「正の相関」の説明です。
- 2が正解。r = −0.3 は負の相関を示しています。
- 3は誤り。相関係数は-1から1の間をとるのでマイナスになることは正常です。
- 4は誤り。相関関係だけでは因果関係(どちらが原因か)は断定できません。睡眠不足だからスマホをいじってしまう可能性もあります。
11.2 データの前処理と可視化
11.2.1 データの前処理
分析の前に必要に応じてデータの前処理を行います。
- ワイド形式にする:Rの cor() 関数や GGally パッケージは、基本的にワイド形式を想定しています。もし手元のデータがロング形式になっている場合はワイド形式に変換しましょう。ワイド・ロング形式やそれらの変換方法についてはこちらのページで解説しています。
- 数値データのみを取り出す:データフレームに文字データ(カテゴリ変数)が含まれている場合はそれを取り除き、分析したい数値データの列だけにしておくと分析がスムーズに進みます。列の抽出には dplyr のselect() 関数などを使うとよいでしょう。
- 欠損値の処理:データに欠損値(NA)が含まれる場合は、どう対処するかを決める必要があります。よく使われる方法としては、「リストワイズ除去」(NA が含まれる行は分析から外す)、「ペアワイズ除去」(計算する相関のペアごとにどの欠損値行を省くかを変える)、「多重代入法」(欠損値を他の列の値から推測して埋める)などがあります。
以下の例は、ペンギンデータに対して数値列の抽出や欠損値を含む行の削除を行っています。
library(tidyverse)
library(palmerpenguins)
# データの前処理
# 1. 数値の列だけを選ぶ (where(is.numeric))
# ※ year(調査年)は数値ですが、相関を見たい変数ではないため除外します
# 2. 欠損値を含む行を削除する (drop_na)
dat = penguins %>%
dplyr::select(-year) %>%
dplyr::select(where(is.numeric)) %>%
drop_na()
# 結果の確認:すべて数値列になっているかチェック
head(dat)
## # A tibble: 6 × 4
## bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
## <dbl> <dbl> <int> <int>
## 1 39.1 18.7 181 3750
## 2 39.5 17.4 186 3800
## 3 40.3 18 195 3250
## 4 36.7 19.3 193 3450
## 5 39.3 20.6 190 3650
## 6 38.9 17.8 181 362511.2.2 可視化の重要性
相関係数を計算する際は図(散布図)を描くことが重要です。相関係数の値だけしか見ない場合、変数間の関連性について誤解をしてしまう場合があるからです。
たとえば、次のような例を考えます。
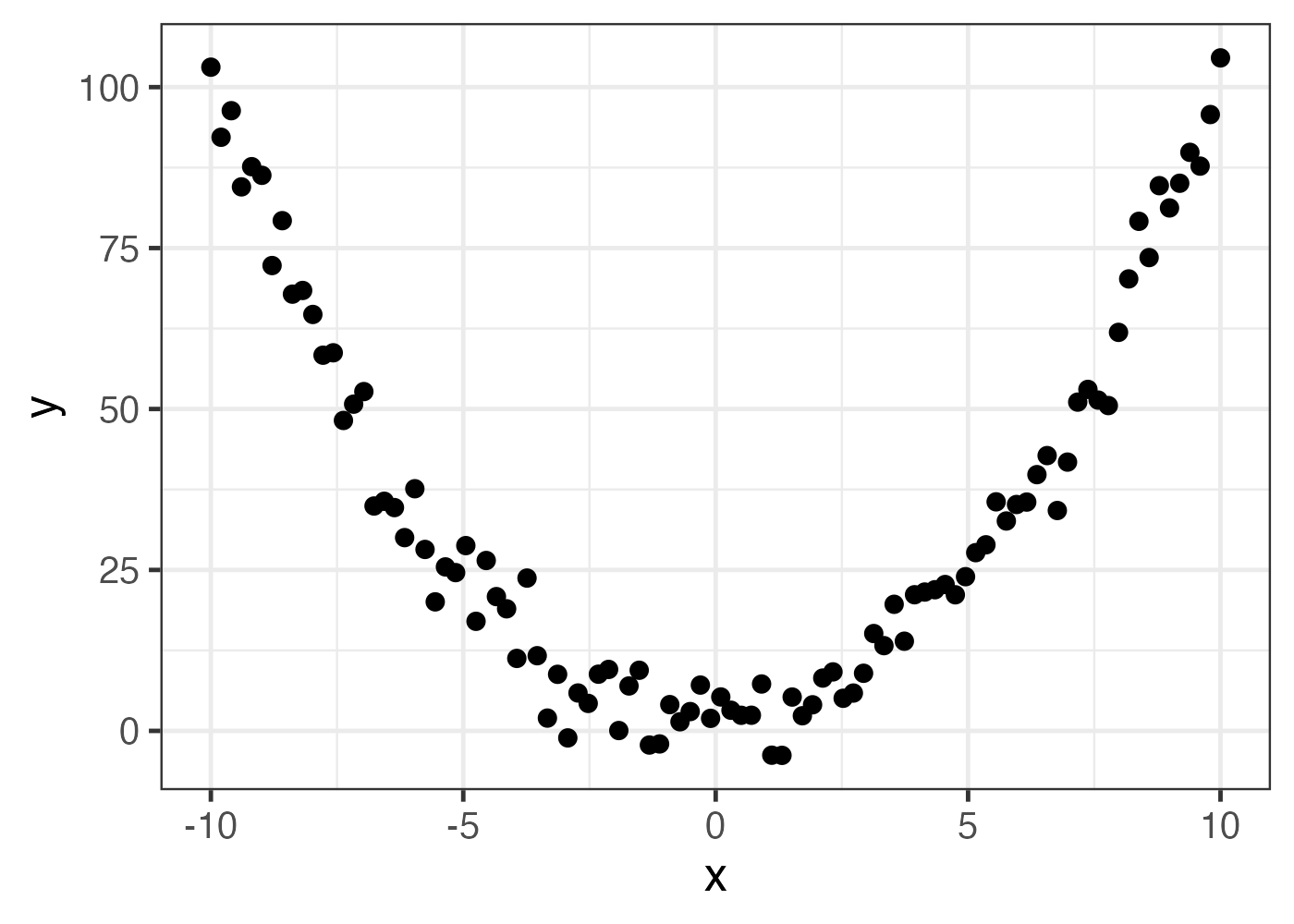
このデータの場合、XとYのピアソンの相関係数を計算すると、ほぼ0になります。しかし、図を見れば明らかなように、この2変数には明白な関連があります。
ピアソンの相関係数は変数間の直線的な関係を想定しているので、上の図のようなU字型の関連性を反映することができません(実際には関連があるのに、相関係数の値は0に近い値になってしまう)。
順位相関係数は値の単調増加や単調減少を想定しているので、曲線的に上昇する(または下降する)ようなデータであれば問題ありませんが、上の図のように下がってから上がるといった関係は反映することができません。
このように、相関係数の値が0に近いからといって変数間に関連性がないとは限らないため、必ず散布図を描いて視覚的にデータの性質を確認する必要があります。
同様に、相関係数の値がある程度高いからといって、変数間に意味のある関連があるとは限りません。これに関してはアンスコムの例が良い例でしょう。
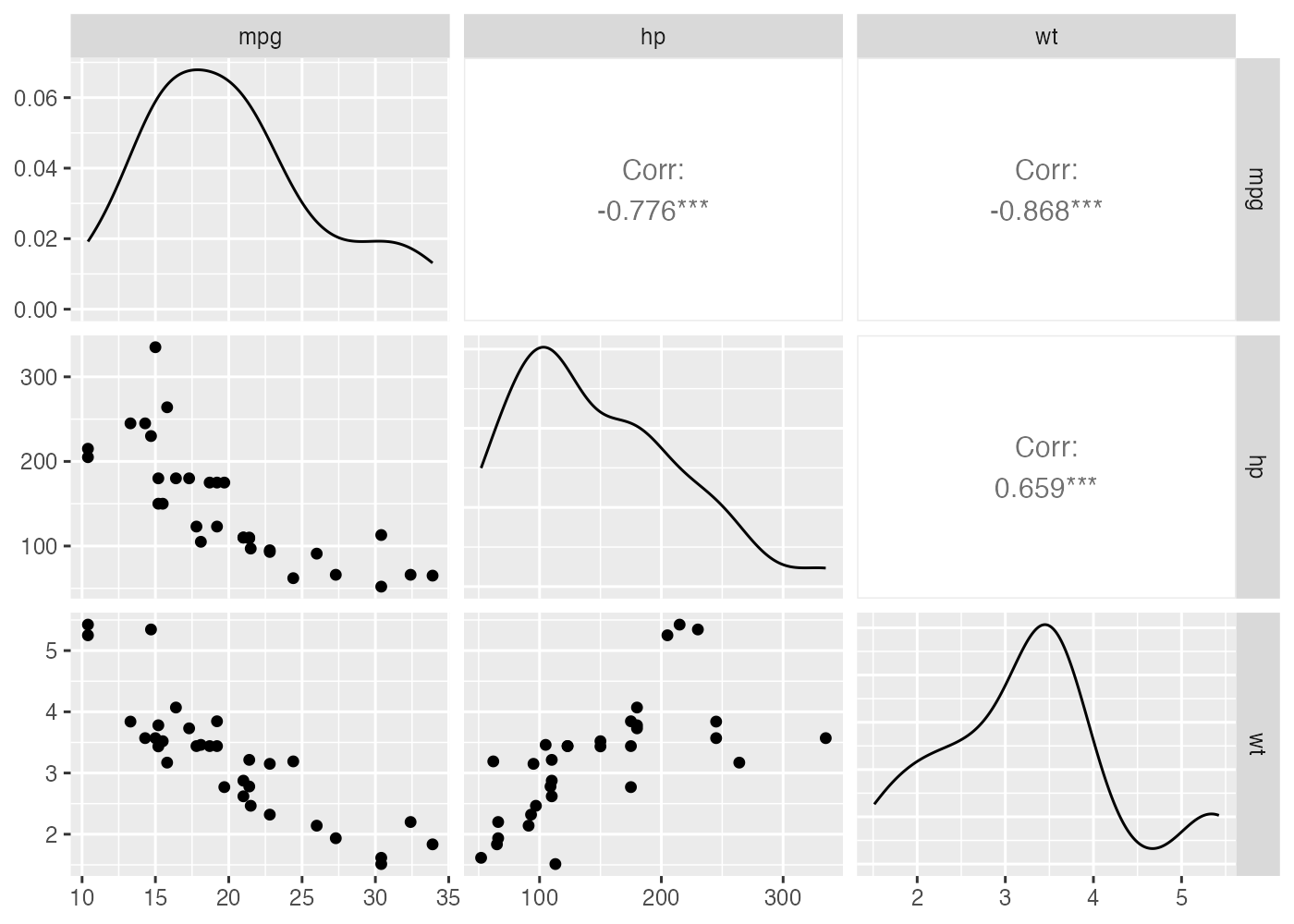
11.2.3 多変量を一望する:散布図行列
変数が2つだけであれば単純な散布図を描けばよいですが、データセットに3つ以上の変数が含まれることもよくあります。変数のすべての組み合わせ(ペア)ごとにひとつずつ図を作るのは面倒です。
そこで役立つのが「散布図行列(Scatter Plot Matrix)」です。
GGally パッケージの ggpairs() 関数を使うと、データフレームに含まれるすべての変数ペアの散布図、ヒストグラム、相関係数を一度に表示できます。
# install.packages("GGally") # 初回のみインストール
library(GGally)
# データの準備(以前の内容と同じ9
dat = palmerpenguins::penguins %>%
dplyr::select(-year) %>%
dplyr::select(where(is.numeric)) %>%
drop_na()
# ペンギンのデータを使って散布図行列を描画
# progress = F は計算中のプログレスバーを非表示にする設定
ggpairs(dat, progress = F)
# 対角線をヒストグラムに変更
# ggpairs(dat, diag = list(continuous = "barDiag"))
# ビンの数を調整する場合
# ggpairs(dat, diag = list(continuous = wrap("barDiag", bins = 15)))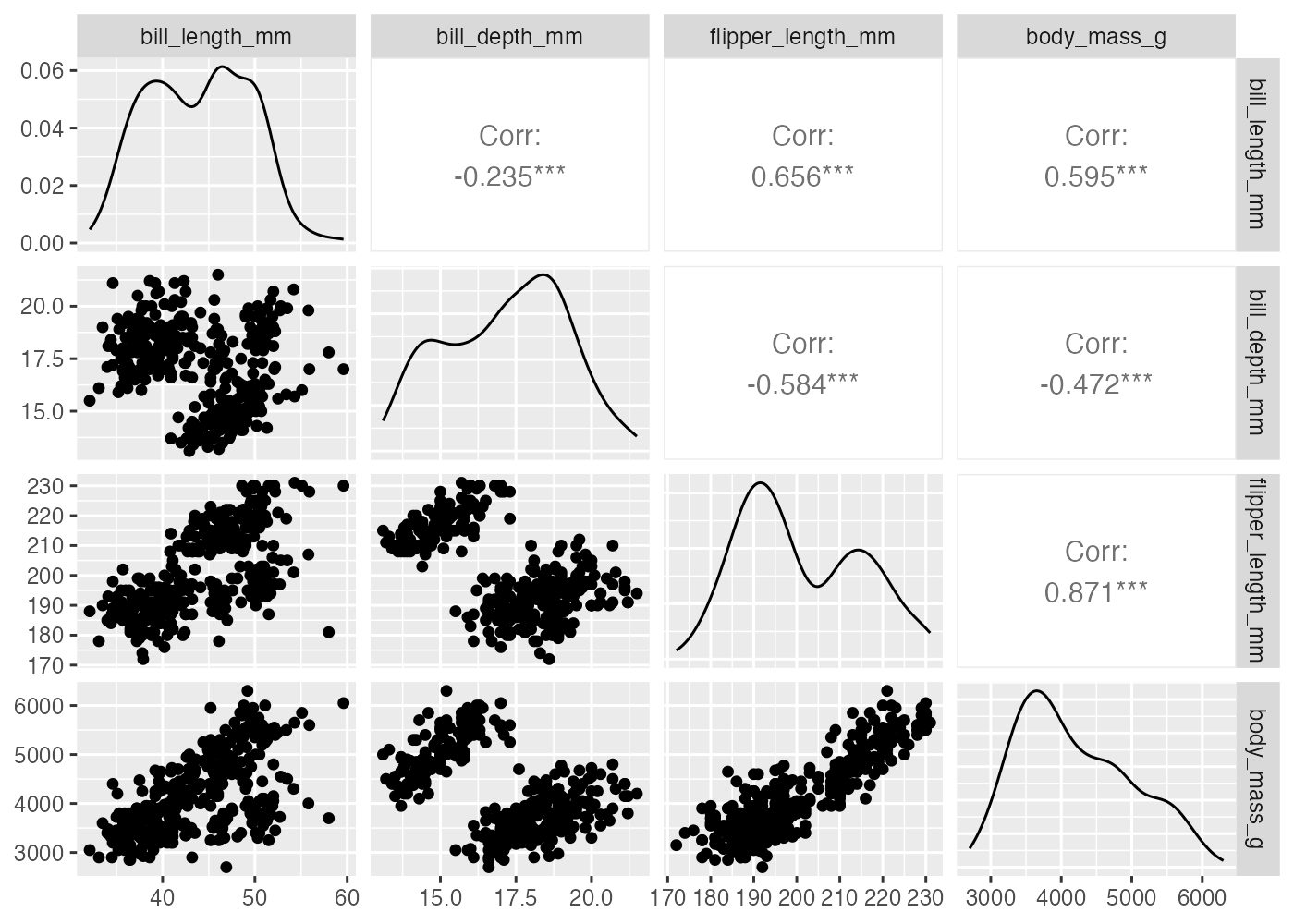
この図ですべての変数間の関係性が一望できます。見方は以下の通りです。
- 対角線(左上から右下):各変数自体の分布(密度プロットやヒストグラム)。正規分布に近いか(山なりか)、データが偏っていないかを確認します。
- 左下側:2変数の散布図。アンスコムの例のような異常がないかを目視でチェックします。
- 右上側:2変数の相関係数。相関の強さが数値で示されます。有意であれば * マークがつきます。
11.2.4 グラフから読み取るべきチェックポイント
散布図行列を出力したら、数値を見る前に以下の3点を重点的にチェックしてください。
- 線形性(Linearity):U字型やカーブを描いている場合、通常の相関分析(ピアソン)は不適切です。
- 外れ値(Outliers):外れ値がある場合、相関係数の解釈は慎重に行う必要があります。
- 層別化の必要性:データ全体で見ると負の相関があるのに、グループごとで調べると正の相関がある場合など、全体と部分で結果が異なる場合があります(シンプソンのパラドクスと呼ばれます)。散布図の中で点群が2つ以上の塊に分かれている場合は要注意です。
11.2.5 確認問題:散布図行列の作成
mtcars データセットを使用し、mpg、hp、wtの3つの変数だけを抽出し、変数 dat_cars に格納してください。
その dat_cars を使って、ggpairs() 関数で散布図行列を描画してください。
11.2.6 確認問題:ggpairs() 関数の応用的利用
ggpairs() 関数では、さまざまな引数を用いて図の見た目を設定できます。また、mapping 引数を使うことで、ggplot2 を使う場合のように、図の見た目のマッピングを行うことができます。
次の例は、ペンギンデータを種によって色分けした散布図行列です。
library(GGally)
library(tidyverse)
library(palmerpenguins)
# 分析対象のデータ(種情報も含めておく)
dat_adv = penguins %>%
dplyr::select(species, bill_length_mm, bill_depth_mm, flipper_length_mm, body_mass_g) %>%
drop_na()
# カスタマイズした散布図行列
ggpairs(
data = dat_adv,
columns = 2:5, # 2列目〜5列目の数値データを使用
mapping = aes(color = species, alpha = 0.5), # 種ごとに色分け
# 対角線の設定:ヒストグラムにする
diag = list(continuous = wrap("barDiag", bins = 20)),
# 左下の設定:散布図の点を小さくする
lower = list(continuous = wrap("points", size = 1.2)),
# 右上の設定:相関係数の文字サイズを調整
upper = list(continuous = wrap("cor", size = 4)),
title = "種でマッピングした場合",
progress = FALSE
) +
theme_bw()
# 比較用:マッピングしない場合
ggpairs(
data = dat_adv, columns = 2:5,
diag = list(continuous = wrap("barDiag", bins = 20)),
lower = list(continuous = wrap("points", size = 1.2)),
upper = list(continuous = wrap("cor", size = 4.5)),
title = "マッピングしていない場合",
progress = FALSE
) +
theme_bw()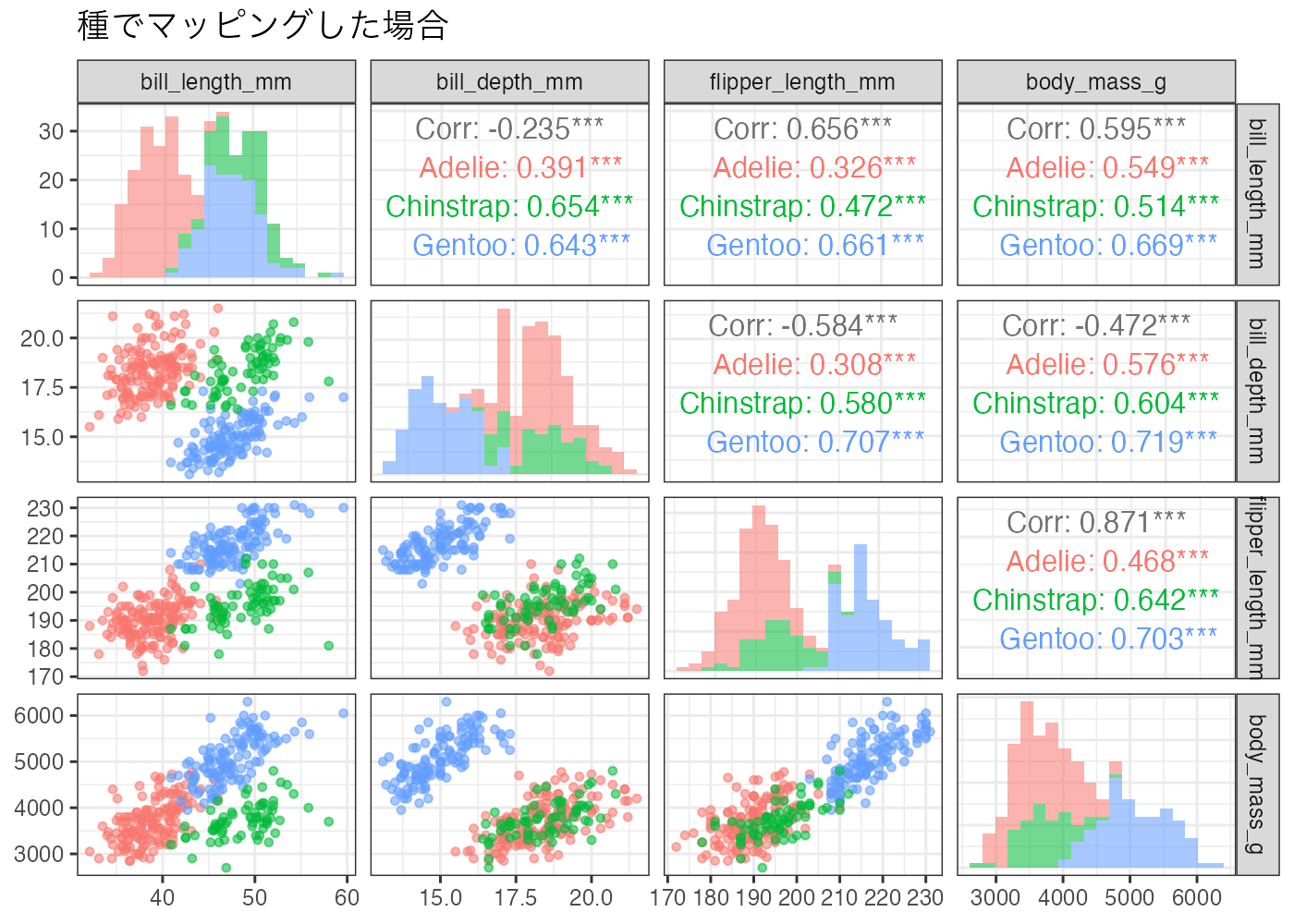
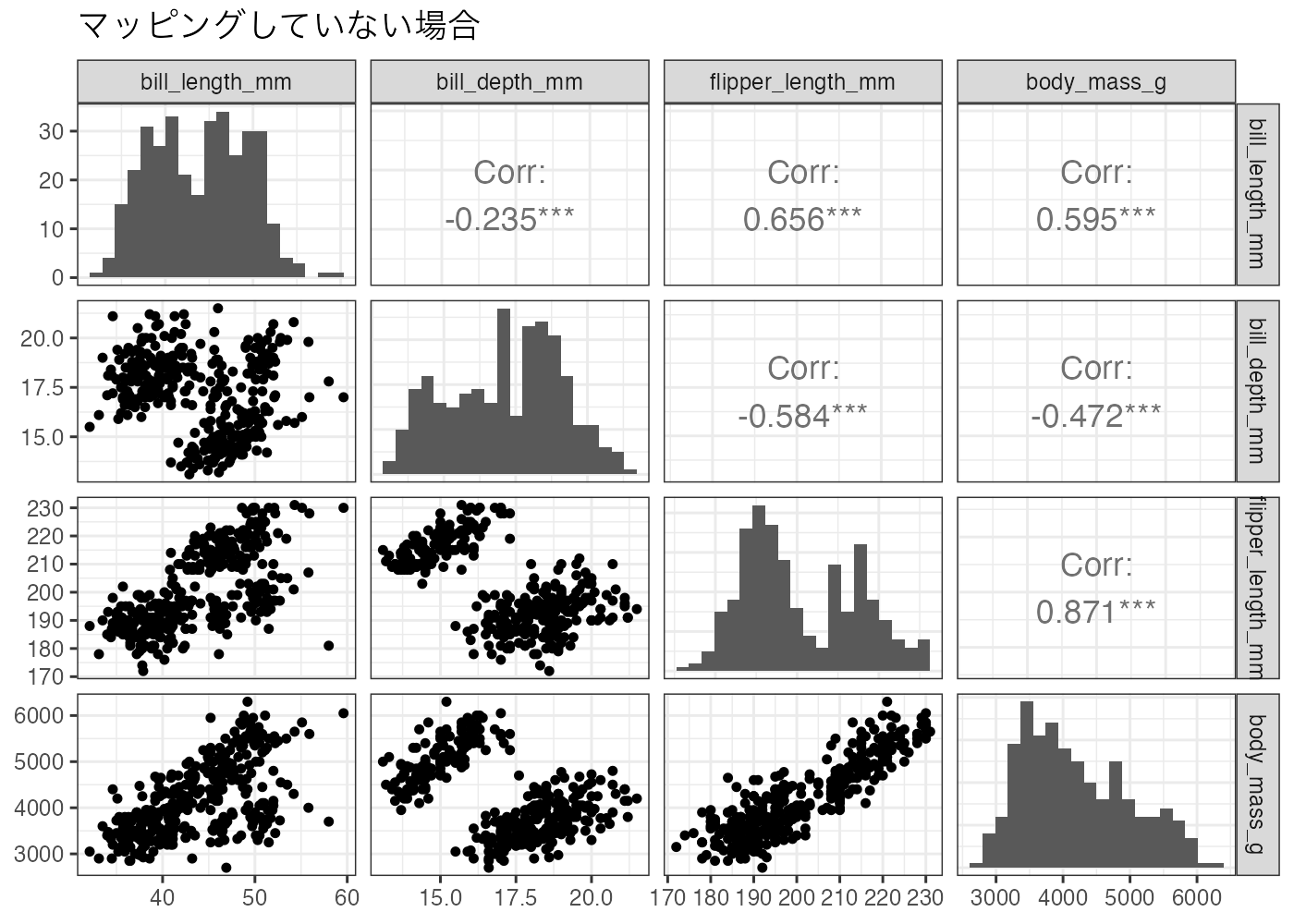
マッピングをすることで、相関係数も種ごとに算出されます。
問題:色でマッピングした図としていない図を比較して、相関係数の値について気づくことを述べてください。
解答と解説を表示
- マッピングをしていない図(全体)では「負の相関」になっている変数の組み合わせが、種ごとに色分け(マッピング)すると「正の相関」に変化している箇所があります。
- 体重(body_mass_g)とクチバシの厚み( bill_depth_mm)の関係を見ると、全体では相関係数は -0.472 で、負の相関を示唆しています。体重が大きいほどクチバシは薄いという意味の相関です。
- しかし、種ごとに見ると、Adelie・Chinstrap・Gentoo のどの種でも、体重とクチバシの厚みは正の相関を持ちます。つまり、体重が大きいほどクチバシも厚いという、生物学的な直感と合致する結果です。
- このような現象は「シンプソンのパラドックス(Simpson’s paradox)」として知られています。
- なぜこのようなことが起きるのでしょうか? Gentoo は、他の種に比べて「体重は重く」て「クチバシは薄い」という特徴を持っています。 一方で Adelie と Chinstrap は、「体重は軽く」て「クチバシは厚い」傾向があります。
- 種を区別せずに混ぜて散布図を描くと、データの塊が「左上(重くて薄い)」と「右下(軽くて厚い)」に配置されるため、全体としては右下がりの関係(負の相関)となってしまうのです。
11.3 相関分析の実施
このセクションでは correlation パッケージを用いて相関分析を行います。この関数は R のデフォルトの cor.test() 関数よりも以下の点で優れています。
- 結果がデータフレーム形式で出力される。
- 入力データに含まれるすべての変数ペアごとの相関を一度に計算できる。
- グループごと(層別)での相関の計算も容易に行える。
- p値の多重比較補正など、有用な機能が多くある。
以下の例ではペンギンデータを対象に、ピアソンの相関係数を計算しています。
データには4つの変数があるので、そのすべての組み合わせについて相関分析が行われ、その結果がデータフレームとして返されます。
# パッケージのインストール(未インストールの場合は実行)
# install.packages("correlation")
library(tidyverse)
library(correlation)
# 分析用データの準備(数値列のみ取り出す)
dat = palmerpenguins::penguins %>%
dplyr::select(where(is.numeric), -year)
# ピアソン相関を変数の総当たりで計算
result = correlation(dat, method = "pearson")
print(result)
## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(340) | p
## -----------------------------------------------------------------------------------
## bill_length_mm | bill_depth_mm | -0.24 | [-0.33, -0.13] | -4.46 | < .001***
## bill_length_mm | flipper_length_mm | 0.66 | [ 0.59, 0.71] | 16.03 | < .001***
## bill_length_mm | body_mass_g | 0.60 | [ 0.52, 0.66] | 13.65 | < .001***
## bill_depth_mm | flipper_length_mm | -0.58 | [-0.65, -0.51] | -13.26 | < .001***
## bill_depth_mm | body_mass_g | -0.47 | [-0.55, -0.39] | -9.87 | < .001***
## flipper_length_mm | body_mass_g | 0.87 | [ 0.84, 0.89] | 32.72 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 342コンソールには結果が表のようにして出力され、その下にはp値の補正方法やデータの件数(観測数)の情報も表示されます。
なお、correlation() 関数は文字列型の列は無視するので、データを準備する際に数値型の列のみを取り出す作業はしなくても構いません。
11.3.1 correlation() 関数の出力
- Parameter1, Parameter2:分析した変数の名前
- r:相関係数
- 95% CI:相関係数の95%信頼区間
- t: 検定統計量(t値)
- df:自由度
- p:p値
ただし、r と t の箇所は、用いた相関の指標によって異なります。
method = "pearson"の場合:r と t値method = "spaerman"の場合:rho(ρ) と S(S統計量)method = "kendall"の場合:tau(τ)と z(z値)
また、df の列は出力されないこともあります。その場合は統計検定量の列名の箇所に自由度の値も記入されています。上の例では t(340) となっており、自由度が 340 だとわかります。
自由度は「データの件数 - 2」で計算できます。上の例では「Observations: 342」と出力されているように、データの件数は 342 なので、自由度 df は 340 になります。
11.3.2 correlation() 関数の引数
以下の引数があります。
method:相関係数の種類
データの性質に応じて適切な指標を選ぶ必要があります。
method = "pearson":ピアソンの積率相関係数(デフォルト)method = "spearman":スピアマンの順位相関係数method = "kendall":ケンドールの順位相関係数
p_adjust:多重検定の補正
p値への多重比較補正に関する設定です。
p_adjust = "holm":Holm法(デフォルト)p_adjust = "bonferroni":ボンフェローニ法p_adjust = "none":補正を行わない
missing:欠損値(NA)の取り扱い
たいていの場合はデフォルト設定(ペアワイズ除去)でよいでしょう。
missing = "keep_pairwise":ペアワイズ除去(デフォルト)missing = "keep_complete":リストワイズ除去
ペアワイズ除去は、計算する2変数ごとにペアが揃っている(NAが含まれていない)行を全て使って相関を計算します。リストワイズ除去は、事前にデータセット全体から NA を含む行を除去してから相関を計算します。この違いのため、ペアワイズ除去では変数ペアごとにN数(データ件数)が異なることがある一方、リストワイズ除去ではどのペアでも同じN数になることが保証されます。
correlation() 関数はデフォルトではデータに含まれるすべての変数ペアごとに相関を計算しますが、select 引数に相関を調べたい列名を指定することで、特定の相関のみを計算することもできます。
dat = palmerpenguins::penguins
result = correlation(dat, select = c("bill_length_mm", "bill_depth_mm"))
print(result)
## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(340) | p
## ----------------------------------------------------------------------------
## bill_length_mm | bill_depth_mm | -0.24 | [-0.33, -0.13] | -4.46 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 34211.3.3 グループごとで相関を分析する
dplyr::group_by() と組み合わせることで、グループごとでの相関係数の計算を行うことができます。以下の例では、bill_length_mm と bill_depth_mm の相関を species ごとに分析しています。
# 分析用データの準備(数値列のみ取り出す)
grouped_results = palmerpenguins::penguins %>%
group_by(species) %>%
correlation(select = c("bill_length_mm", "bill_depth_mm"))
print(grouped_results)
## # Correlation Matrix (pearson-method)
##
## Group | Parameter1 | Parameter2 | r | 95% CI | t | df | p
## -----------------------------------------------------------------------------------------
## Adelie | bill_length_mm | bill_depth_mm | 0.39 | [0.25, 0.52] | 5.19 | 149 | < .001***
## Chinstrap | bill_length_mm | bill_depth_mm | 0.65 | [0.49, 0.77] | 7.01 | 66 | < .001***
## Gentoo | bill_length_mm | bill_depth_mm | 0.64 | [0.53, 0.74] | 9.24 | 121 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 68-15111.3.4 結果の記述
論文では相関係数の値、自由度、そしてp値を記述します。相関係数の95%信頼区間も書くとよいでしょう。
「ジェンツーペンギンにおいて、クチバシの長さと体重の間に有意な正の相関がみられた(r(121) = .64, 95% CI [.53,.74], p < .001)。」
相関係数やp値は1を超えないため、.59 のように冒頭の0を省略して書きます。また、記号はイタリック体にします。
相関係数の記号にピアソンの相関係数の場合は r を使いますが、スピアマンでは ρ(ロー)、ケンドールでは τ(タウ)を使うようにします。
なお、相関関係が見られたからといって、それが因果関係を示しているとは限りません。したがって、単に相関を発見しただけの場合は、以下のような表現は避けるようにします。
- ×「XがYに影響を与えていることが分かった」
- ×「Xを増やせばYも増える」
- ×「XがYの原因である」
以下のような表現を使うようにしましょう。
- ◯「XとYには関連が見られた」
- ◯「Xが高い傾向にあるとき、Yも高い傾向にある」
- ◯「有意な相関が認められた」
11.3.5 グラフの作成
通常の散布図に加えて、回帰直線や相関係数の値を図に追加するとよいでしょう。
ggpubr パッケージの stat_cor() 関数を使うと相関係数とp値をグラフ内に書き込むことができます。また、theme_pubr() はggpubr パッケージが提供するテーマで、図を論文でよく使われるスタイル(見た目)にできます。
library(ggpubr)
fig = ggplot(dat, aes(x = bill_length_mm, y = body_mass_g)) +
geom_point(alpha = 0.6) +
geom_smooth(method = "lm", color = "blue", fill = "lightblue") +
stat_cor(method = "pearson", label.x = 35, label.y = 6000,
p.accuracy = 0.001, size = 5) +
theme_pubr() +
labs(x = "クチバシの長さ (mm)", y = "体重 (g)")
# グラフの表示
print(fig)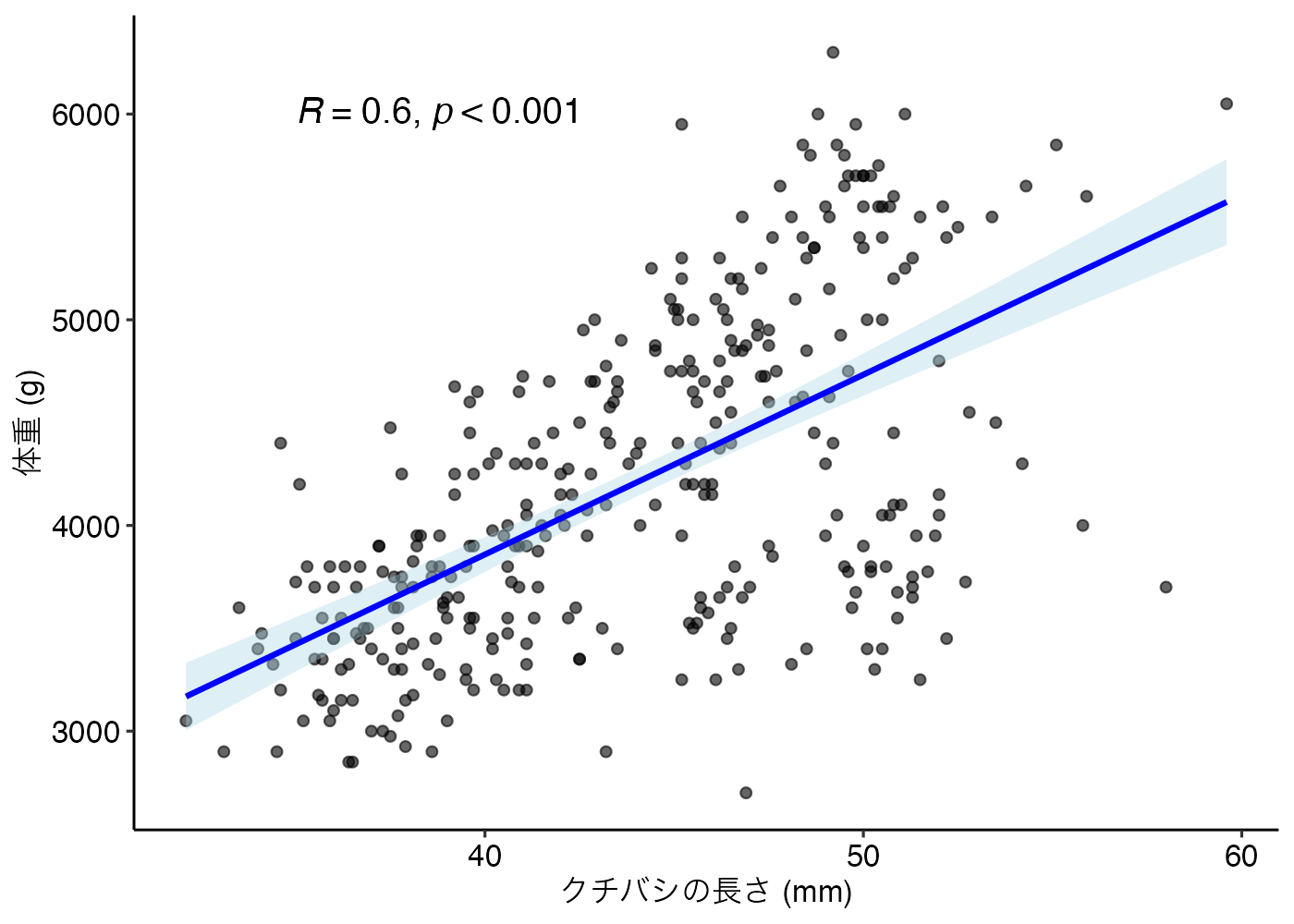
ただし、stat_cor() 関数がグラフに表示するp値は、基本的に「補正なし(p_adjust="none")」の値です。correlation() 関数で多重検定の補正を行った場合、表の数値とグラフの数値が異なる場合があることに注意してください。
補正後のp値を表示させたい場合は、geom_text() 関数を使う方法があります。
11.3.6 確認問題:相関分析
Rに標準で入っている mtcars データセット(自動車のスペックデータ)を使用します。 「車の重量(wt)」と「燃費(mpg)」の間にどのような関係があるかを調べるために、以下の手順で分析を行ってください。
- mtcars データを読み込み、変数 dat_cars に格納する。
- correlation() 関数を使って、相関係数やp値などを計算する。
- 出力された結果(r, 95% CI, p)をもとに、この2変数の関係を記述する。 (記述例:「〇〇と〇〇の間には、有意な…」)
解答と解説を表示
library(tidyverse)
library(correlation)
# データの準備
dat_cars = mtcars
# 相関の計算
result = dat_cars %>%
correlation(select = c("wt", "mpg"))
print(result)
## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(30) | p
## --------------------------------------------------------------------
## wt | mpg | -0.87 | [-0.93, -0.74] | -9.56 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 32
記述例:
車の重量と燃費の間には、有意な負の相関がみられた (r(30) = −.87, 95% CI [−.93, −.74], p < .001)。11.3.7 確認問題:グループ別の相関分析
Rに標準で入っている iris データセット(アヤメの計測データ)を使用します。 このデータには Species(品種)というグループ変数が含まれています。
「品種ごと」に、「がく片の長さ(Sepal.Length)」と「花弁の長さ(Petal.Length)」の相関関係を計算してください。
解答と解説を表示
library(tidyverse)
library(correlation)
# 方法1
result = iris %>%
group_by(Species) %>%
correlation(select = c("Sepal.Length", "Petal.Length"))
# 方法2
result = iris %>%
group_by(Species) %>%
correlation() %>%
filter(Parameter1 == "Sepal.Length", Parameter2 == "Petal.Length")
print(result)
## # Correlation Matrix (pearson-method)
##
## Group | Parameter1 | Parameter2 | r | 95% CI | t(48) | p
## -----------------------------------------------------------------------------------
## setosa | Sepal.Length | Petal.Length | 0.27 | [-0.01, 0.51] | 1.92 | 0.202
## versicolor | Sepal.Length | Petal.Length | 0.75 | [ 0.60, 0.85] | 7.95 | < .001***
## virginica | Sepal.Length | Petal.Length | 0.86 | [ 0.77, 0.92] | 11.90 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 50方法2では、すべての変数を用いて相関を計算し、その結果から必要な行のみを取り出しています。今回の問題ではそうする意義は特にありませんが、すべての相関の結果を別の変数に格納しておき、知りたい変数ペアの情報のみをその変数から取り出すといった処理をする際には filter() を使った書き方が便利です。
11.4 多変量データの相関分析
分析対象のデータセットに多数の変数(列)が含まれている場合があります。変数の数が少なければ、上で紹介した散布図行列を用いて結果を確認しやすいです。しかし、変数の数がたとえば10個ある場合は、45個の散布図が作成されることになり、複雑過ぎて理解が困難になります。
このセクションでは、多数の変数を持つデータ(多変量データ)の相関関係を分析し、ヒートマップやネットワーク図によってわかりやすく可視化する方法について説明します。
まずは必要なパッケージとデータを準備します。
# install.packages("see") # easystatsの可視化パッケージ
# install.packages("gt") # 表作成パッケージ
# install.packages("ggraph") # ネットワーク図の描画に必要
library(tidyverse)
library(correlation)
library(see)
library(gt)
# データの準備
# 6つの数値変数を含むデータセットを作成します
dat = palmerpenguins::penguins %>%
dplyr::select(-c(island, sex)) %>%
drop_na()11.4.1 相関行列の作成
可視化の前に、データに含まれるすべての変数間の相関を計算したデータフレームを作成する必要があります。これは上でも行ったように、correlation() 関数を使えばすぐにできます。
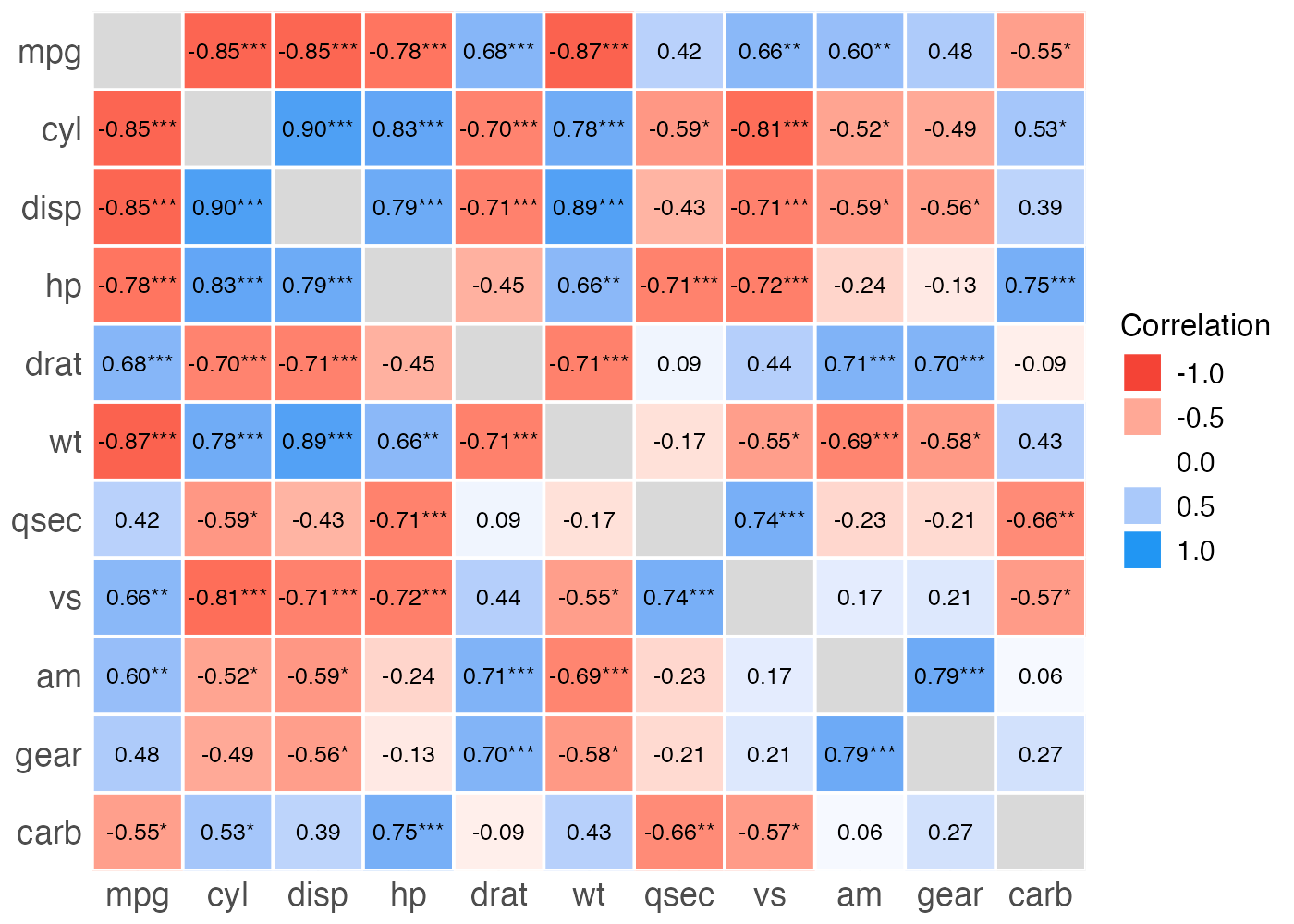
11.4.2 ヒートマップによる可視化
多変量の相関を可視化する際によく使われるのはヒートマップです。相関係数の値を色で表現することで、相関の正負や強弱を直感的に把握できます。
library(see)
# ヒートマップの描画(最小限バージョン)
# results %>%
# summary(redundant = TRUE) %>%
# plot()
# ヒートマップの描画(調整バージョン)
results %>%
summary(redundant = TRUE) %>% # 結果を行列の形に変換する
plot(
type = "tile", # タイル型(ヒートマップ)を指定
show_values = TRUE, # 相関係数の数値を表示
show_p = TRUE, # 有意な場合に「*」を表示
digits = 2 # 小数点以下の表示桁数
) +
scale_fill_gradient2(
low = "red", mid = "white", high = "steelblue",
midpoint = 0, limit = c(-1, 1), name = "相関係数"
) +
coord_fixed() + # セルを正方形にする
labs(title = NULL) + # 図のタイトルを消す
theme_minimal(base_size = 12) + # 文字サイズの調整
theme(
axis.text.x = element_text(size = 13, angle = 45, hjust = 1),
axis.text.y = element_text(size = 13),
legend.title = element_text(size = 12),
legend.text = element_text(size = 11)
)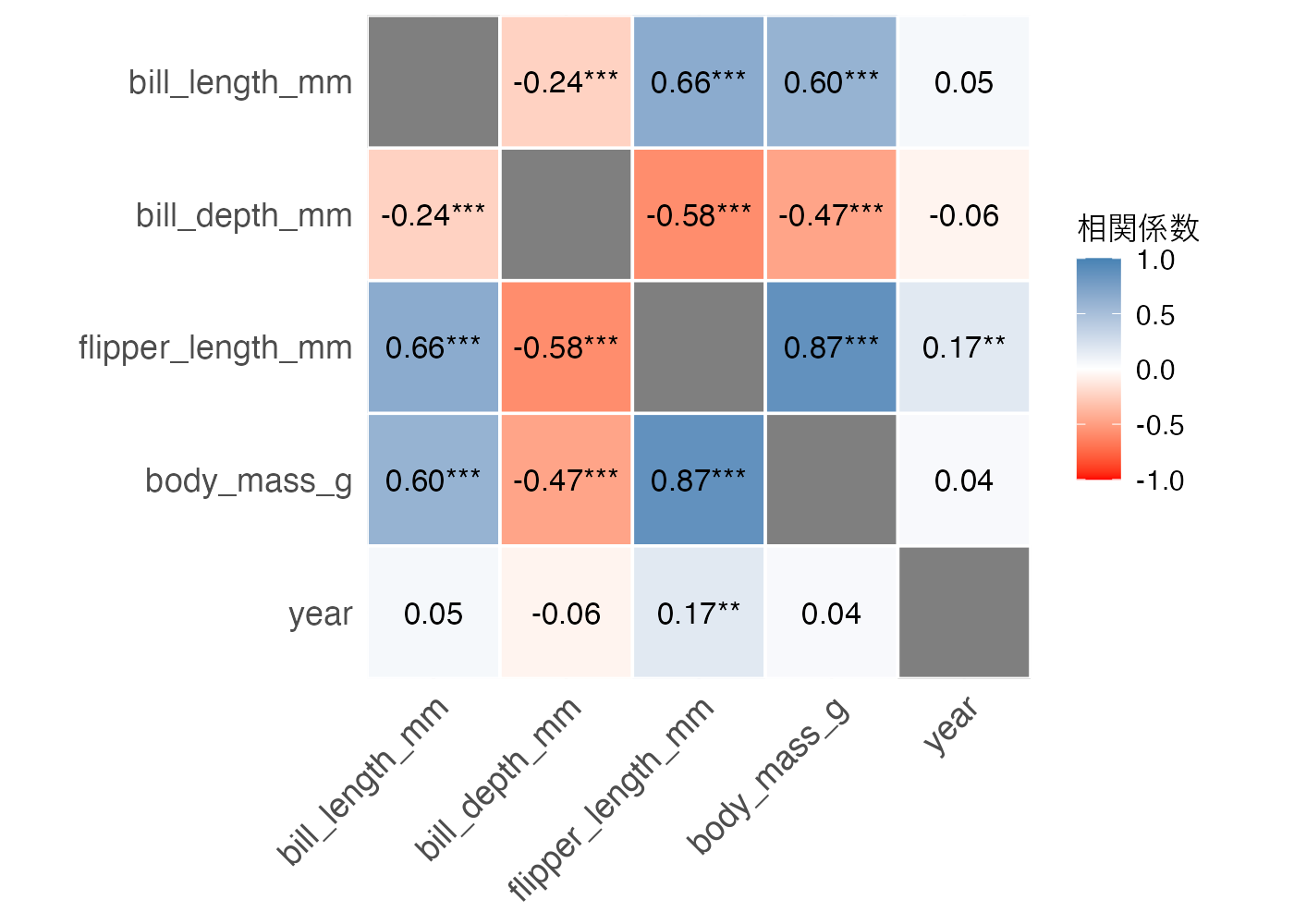
作図の前に、correlation() の結果(results)を summary() 関数を使って相関係数の値を表の形式にしています。ここでredundant = TRUEという指定をすると対角線の両側が可視化され、ここを FALSE に指定すると片側だけが表示されるようになります。
plot() 関数の引数で表示される情報を変更できますが、たいていはデフォルトのままで構わないでしょう。
scale_fill_gradient2() 関数を使うことで配色を決めることができます。
theme() 関数で文字に関する細かい設定をしています。特に、X軸のラベルの angle を 45° に指定することでラベル同士が重なってしまうのを回避しています。
11.4.3 相関ネットワーク図
ヒートマップは個々の値を見るのに適していますが、変数同士がどういうグループ(クラスタ)を作っているかという構造を見るにはネットワーク図が適しています。
correlation() の結果(results)を、summary() を通さずにそのまま plot() すると、自動的にネットワーク図になります。
library(see)
# 相関ネットワーク図の描画
results %>%
plot(show_data = "points") +
scale_edge_color_gradient2(
low = "red", mid = "white", high = "steelblue", # 色設定
midpoint = 0, limit = c(-1, 1), # 範囲を-1から1に
name = "Correlation"
)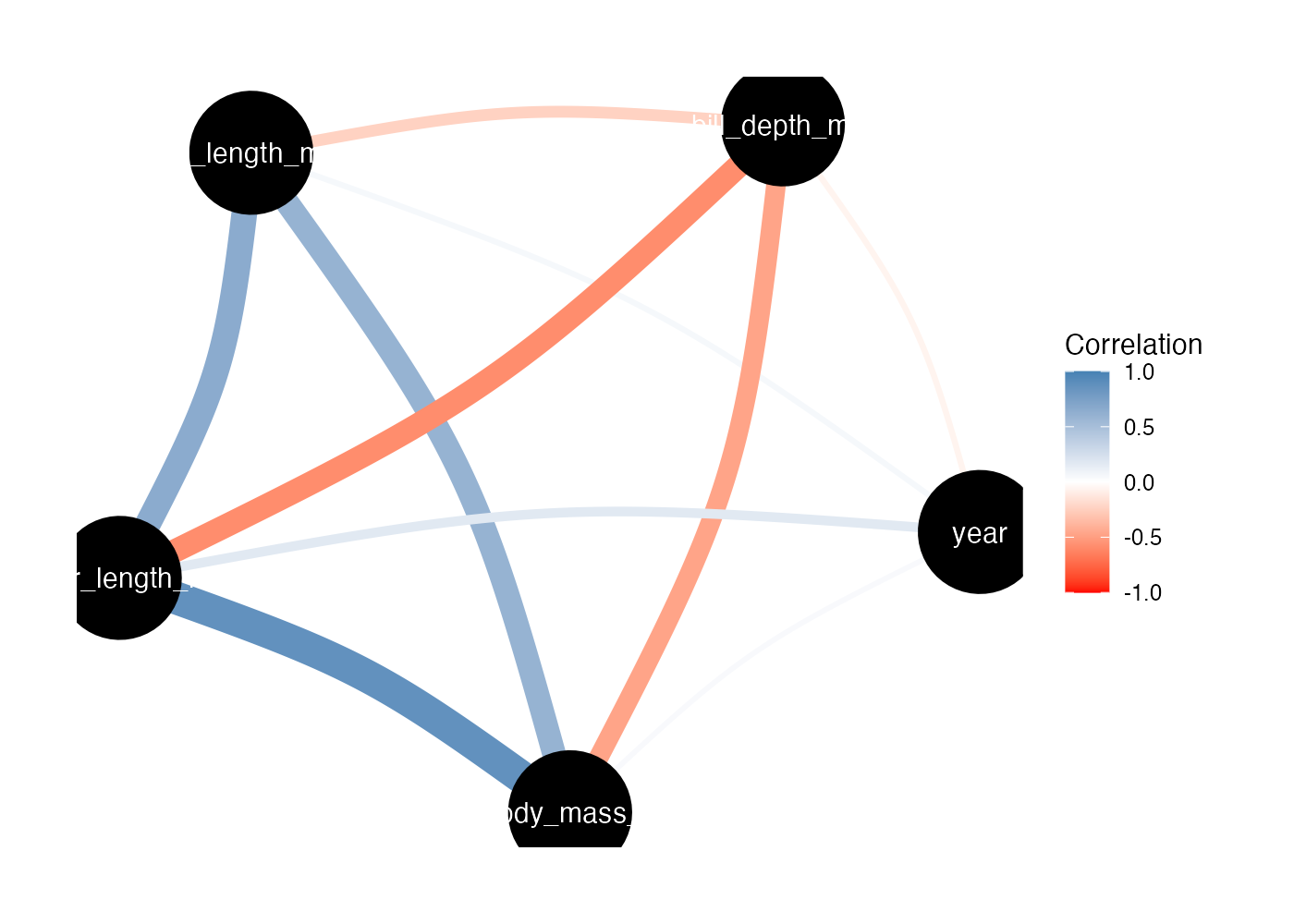
丸が各変数で、相関係数が線として表現されています。
11.4.4 相関行列の表の作成
library(gt)
table_output = results %>%
summary(redundant = TRUE) %>%
gt() %>%
fmt_number(decimals = 2)
# 表の表示
plot(table_output)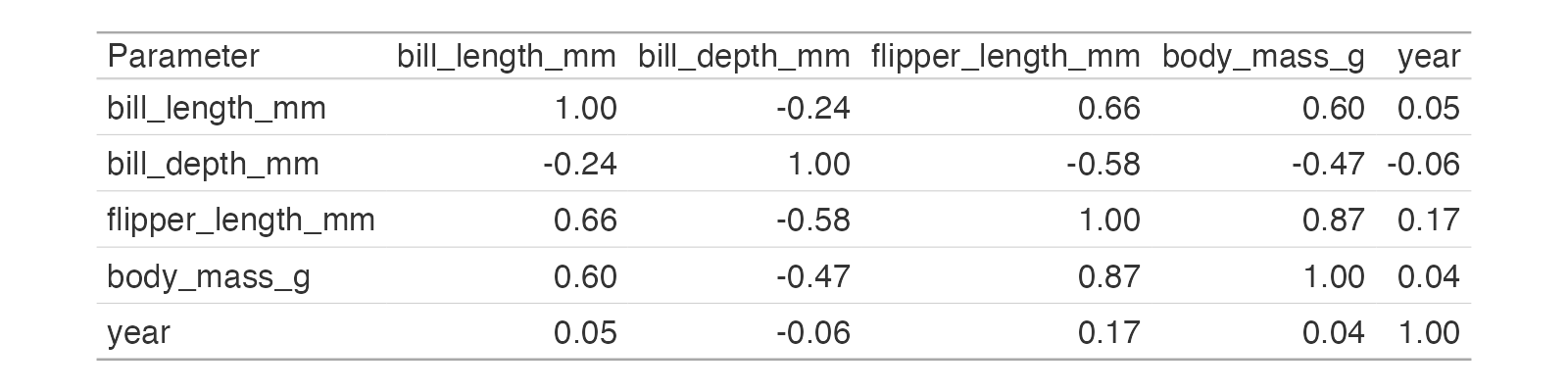
11.4.5 相関係数のドットプロット
どのペアの相関が一番強いのかをランキング形式で見たいという場合には、ドットプロットが便利です。
results %>%
ggplot(aes(x = r, y = reorder(paste(Parameter1, " - ", Parameter2), r))) +
geom_point() +
geom_errorbar(aes(xmin = CI_low, xmax = CI_high), width = 0.2) +
geom_vline(xintercept = 0, linetype = "dashed") +
labs(y = "Pairs", x = "Correlation (r)") +
scale_x_continuous(limits = c(-0.9, 0.9), breaks = 0.2 * (-4:4)) +
theme_bw()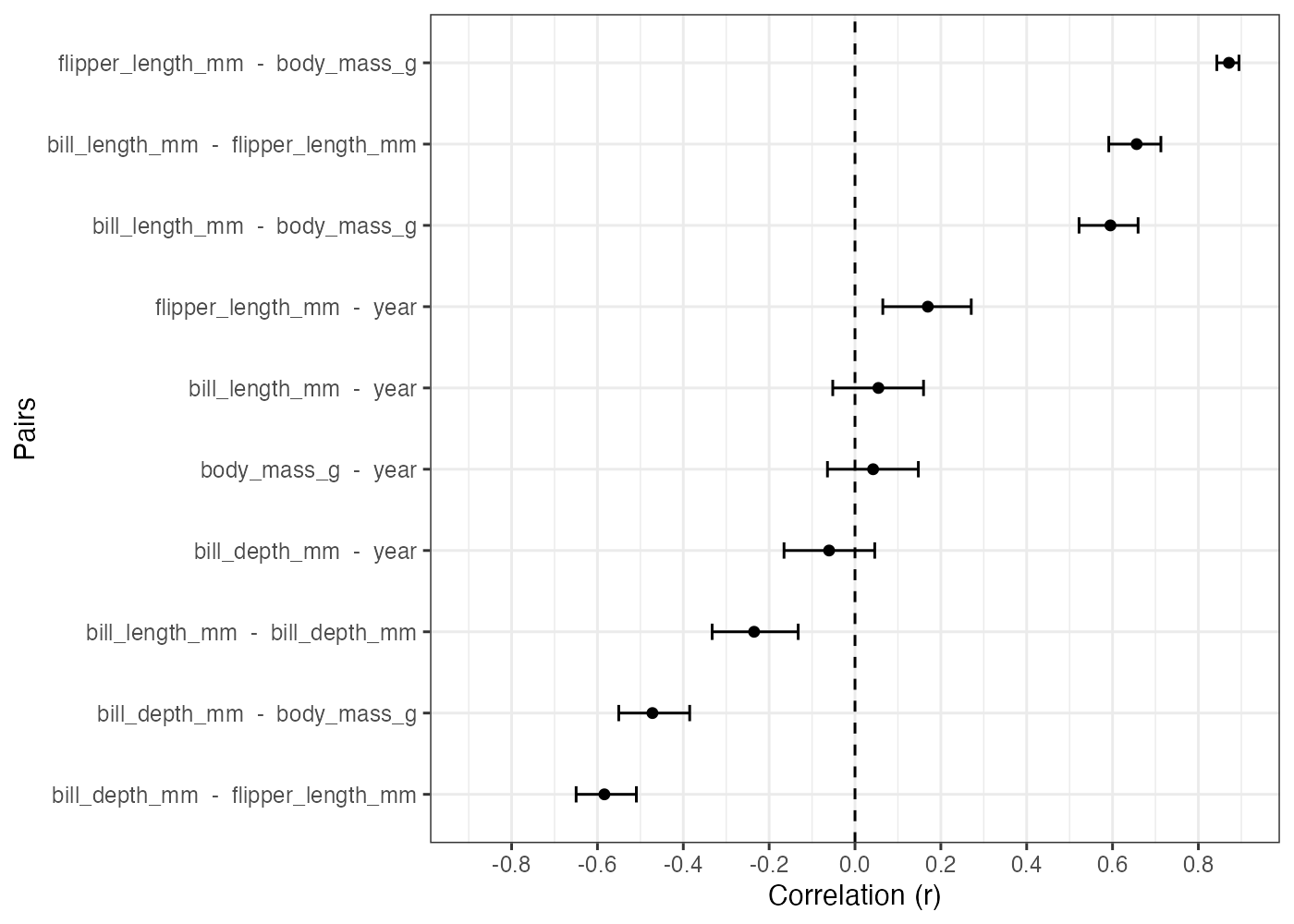
これにより、相関係数の点推定値だけでなく、信頼区間も含めて比較することができます。
11.5 偏相関分析
「アイスクリームの売上」と「水難事故の発生件数」には正の相関があります。しかし、この2つの変数の間に因果関係があるわけではありません。実際には、「気温」などの第三の変数(交絡因子)があると考えられます。
暑くなるとアイスが売れるようになり、また暑くなると泳ぐ人も増える(よって水難事故も増える)という個別の因果関係があります。それらが合わさることで、アイスの売り上げと水難事故の件数の間にも見かけ上の関連(相関関係)が見られるようになります。
偏相関分析はこのような状況で活躍します。
11.5.1 偏相関分析とは何か
偏相関係数(Partial Correlation Coefficient)とは、「ある変数(Z)の影響を統計的に取り除いた上での、2つの変数(XとY)の間の相関係数」のことです。
先ほどの例で言えば、気温の影響を取り除いた時に、それでもなおアイスの売り上げと水難事故の件数に相関関係があるのかを、偏相関によって調べることができます。
以下の架空のデータを用いて偏相関の計算をしてみましょう。
library(tidyverse)
library(correlation)
library(GGally) # 散布図行列を描くパッケージ
# データの生成
set.seed(123)
n = 200
Temp = rnorm(n, mean = 30, sd = 5)
IceCream = 50 * Temp + rnorm(n, mean = 0, sd = 200)
Accidents = 2 * Temp + rnorm(n, mean = 0, sd = 10)
dat_spurious = data.frame(Temp, IceCream, Accidents)
# 散布図行列
ggpairs(dat_spurious,
lower = list(continuous = wrap("points", alpha = 0.5, color = "steelblue")),
upper = list(continuous = wrap("cor", size = 5))) +
theme_bw()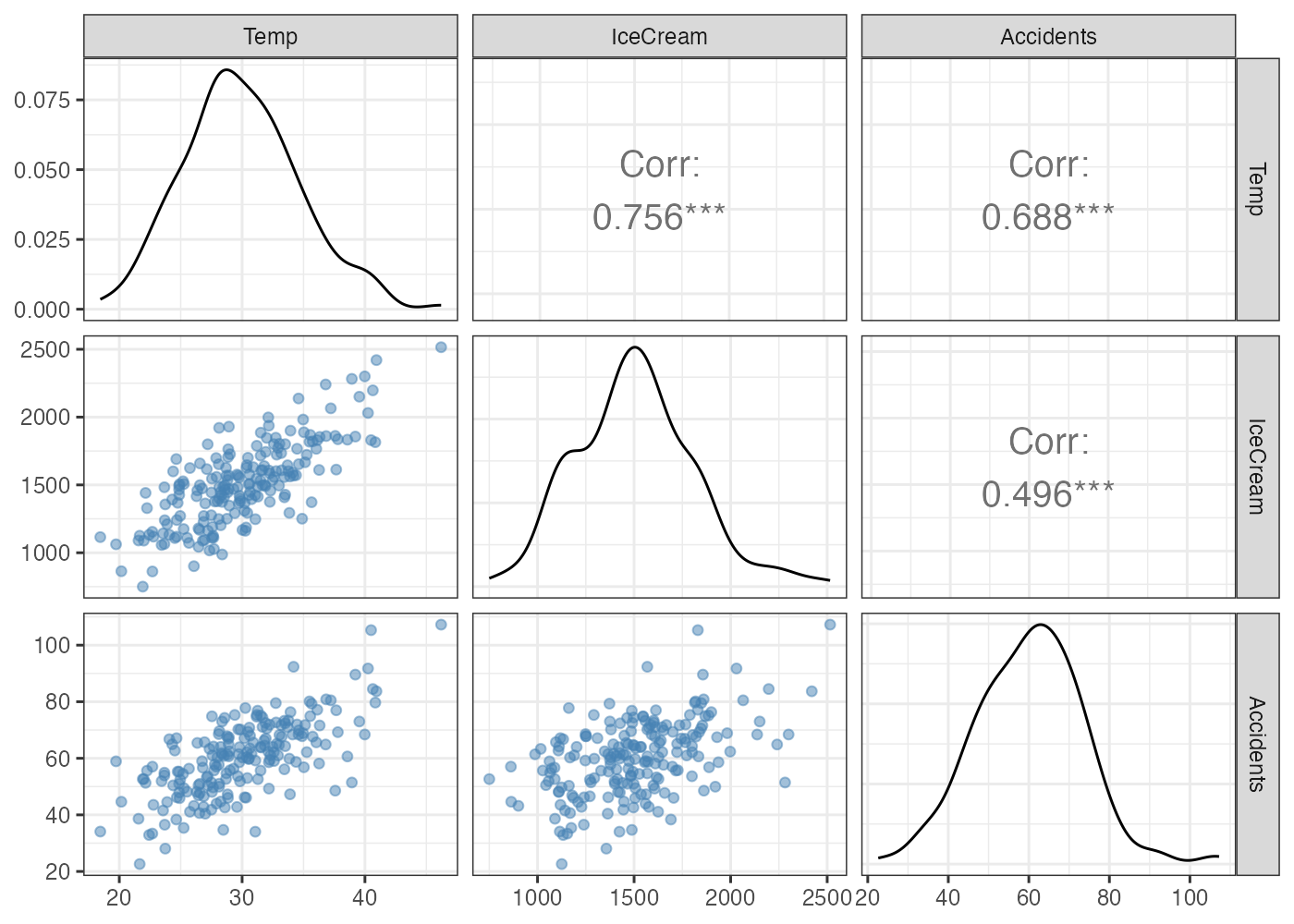
このデータでは、気温(Temp)、アイスの売り上げ(IceCream)、水難事故件数(Accidents)の3つの変数がお互いに正の相関を示しています。
アイスの売り上げと水難事故件数のピアソン相関は約0.5です。
次に、偏相関係数を計算します。
correlation() 関数においてpartial = TRUEを指定することで偏相関係数を計算できます。
# 相関係数の計算
dat_spurious %>%
correlation()
## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(198) | p
## ------------------------------------------------------------------
## Temp | IceCream | 0.76 | [0.69, 0.81] | 16.27 | < .001***
## Temp | Accidents | 0.69 | [0.61, 0.75] | 13.34 | < .001***
## IceCream | Accidents | 0.50 | [0.38, 0.59] | 8.03 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 200
# 偏相関行列の計算
dat_spurious %>%
correlation(partial = TRUE)
## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(198) | p
## --------------------------------------------------------------------
## Temp | IceCream | 0.66 | [ 0.57, 0.73] | 12.33 | < .001***
## Temp | Accidents | 0.55 | [ 0.45, 0.64] | 9.29 | < .001***
## IceCream | Accidents | -0.05 | [-0.19, 0.09] | -0.74 | 0.462
##
## p-value adjustment method: Holm (1979)
## Observations: 200偏相関係数の場合、アイスと事故の相関はほぼ0になりました。気温の影響を取り除くと、アイスと事故には相関関係が見られないことがわかります。
また、気温とアイスや気温と事故の相関係数の値にも変化が生じています。これらの相関を計算する際にも、第3変数の影響を取り除いているからです。つまり、気温とアイスの相関を計算する際には事故の影響を取り除いています。気温と事故の相関を計算する際にはアイスの影響を取り除いています。
11.5.2 偏相関のしくみ
偏相関の計算方法を簡単に説明します。
偏相関係数とは、「ある変数(Z)の影響を統計的に取り除いた上での、2つの変数(XとY)の間の相関係数」のことです。ここで、「Zの影響を取り除く」とは、具体的には、「X や Y から、Z で説明できる部分を引き算する」ということです。
- 予測する:回帰分析を使って、Z から X や Y を予測する直線を引きます。
- 引き算する:実際のデータから予測値を引きます。残ったズレが「残差」です。
残差 = 実測値 - 予測値
- 相関を見る: こうして得られた「X の残差」と「Y の残差」の相関が、偏相関です。
実際に残差を計算し、その値を使って散布図行列を描いてみます。
# アイスの売上のうち、気温では説明できない部分(残差)
resid_IceCream = resid(lm(IceCream ~ Temp, data = dat_spurious))
# 事故数のうち、気温では説明できない部分(残差)
resid_Accidents = resid(lm(Accidents ~ Temp, data = dat_spurious))
# 残差データの作成(Temp自体はそのまま統制変数として残します)
dat_resid = data.frame(
Temp = dat_spurious$Temp,
IceCream_Resid = resid_IceCream,
Accidents_Resid = resid_Accidents
)
# 残差での散布図行列
ggpairs(dat_resid,
lower = list(continuous = wrap("points", alpha = 0.5, color = "steelblue")),
upper = list(continuous = wrap("cor", size = 5))) +
theme_bw()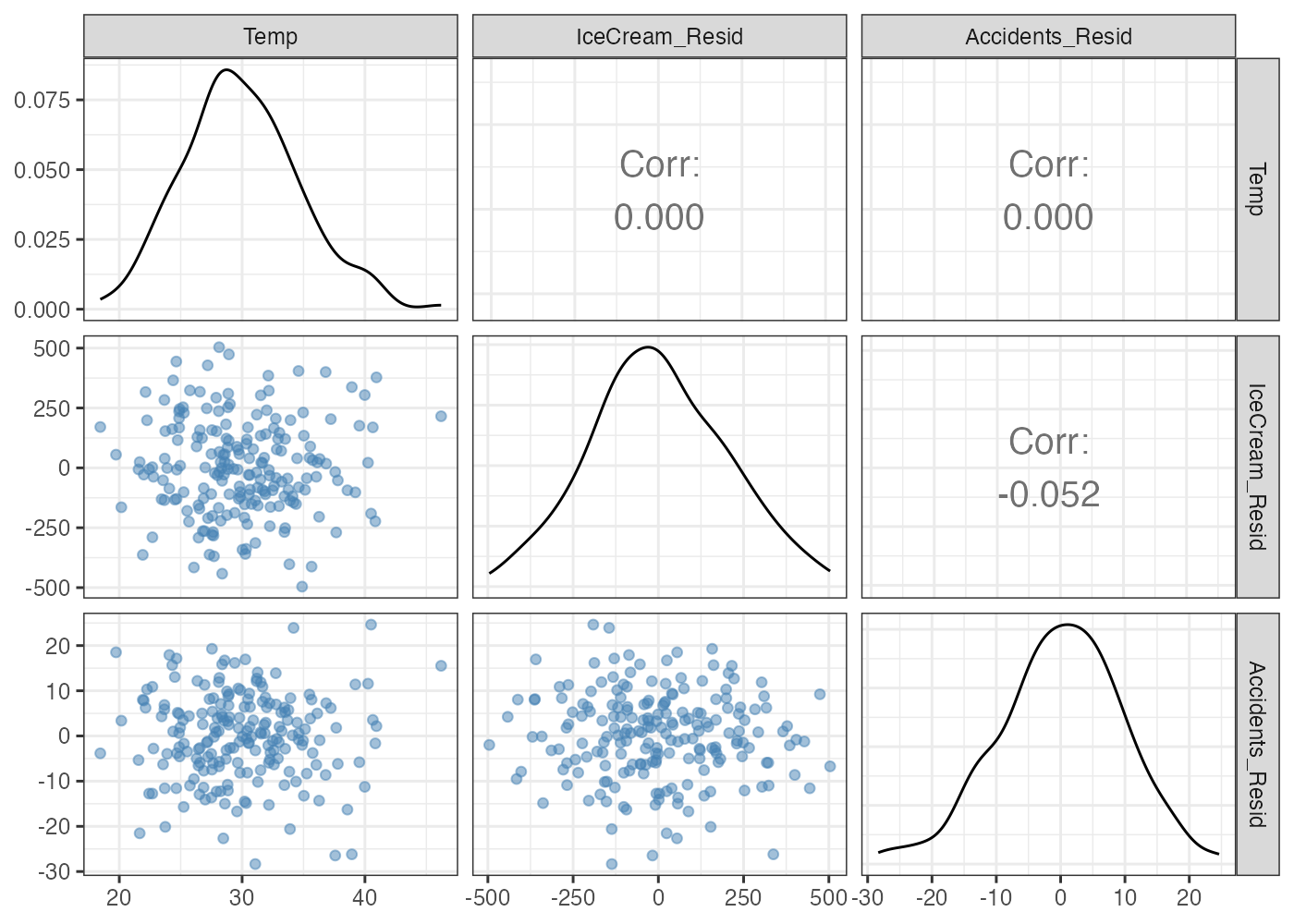
アイスと事故の相関は -0.05 になっており、散布図でも無相関の見た目をしています。
なお、気温はアイスの残差や事故の残差とは無相関になります。気温によってアイスや事故を回帰したので、これは必然的な結果です。
11.5.3 相関と偏相関の使い分け
3つ以上の変数を扱う際、「通常の相関」と「偏相関」のどちらを見るべきなのでしょうか? これは「分析の目的」によって決まります。
相関係数を使う場合
- 原因が何であれ、「アイスが売れている日は事故が多い」という事実(現象)は正しいと言えます。現象をそのまま記述したい場合や、ある変数から別の変数を予測したい場合には通常の相関係数を使います。
偏相関係数を使う場合
- 「アイスを販売禁止にすれば事故は減るか?」という介入の効果を知りたい場合など、見かけの相関の背後にある因果関係やメカニズムを知りたい場合は、第三変数(交絡因子)の影響を統制した上での変数間の関連を知る必要があるので、偏相関を使います。
11.5.4 確認問題
小売店のデータを分析したところ、「店舗の広さ」と「売上」には正の相関がありました。売上を増やすためには店舗サイズを大きくするとよいのかもしれません。
しかしよく調べてみると、「取扱商品数」が多い店ほど店舗も広く、売上も高いこともわかりました。
「店舗を広くしさえすれば(商品は増やさなくても)、売上は伸びるのか?」という疑問に答えるために、見るべき指標はどれですか?
- 「店舗の広さ」と「売上」の通常の相関係数
- 「取扱商品数」を統制した、「店舗の広さ」と「売上」の偏相関係数
- 「売上」を統制した、「店舗の広さ」と「取扱商品数」の偏相関係数
- 「店舗の広さ」を統制した、「売上」と「取扱商品数」の偏相関係数
解答と解説を表示
解答: 2
「商品が増えたから売れた」という要因を除外して、「広さそのものの効果」を知りたいため、商品数を統制変数とした偏相関分析(2)を行うのが適切です。もしこの偏相関が0に近ければ、「ただ店を広げても、商品を増やさなければ売上は伸びないだろう」と判断できます。
11.5.5 確認問題
ある小学校で、すべての生徒(全学年の生徒)のデータを分析したところ、「足のサイズ」と「漢字のテストの点数」の間に非常に強い正の相関(r = 0.8)が見つかりました。しかし、「足が大きいほど漢字が得意になる」と結論づけるのは間違いです。
この場合、どのような「第三の変数(交絡因子)」を統制すれば、この相関は消えると考えられますか?
解答と解説を表示
解答例: 学年(または年齢)
- 高学年になるほど体格が成長して足が大きくなり、同時に学習量も増えて漢字も書けるようになります。
- 「学年」の影響を取り除いて(同じ学年の中だけで)分析(偏相関を計算)すれば、足のサイズと漢字の点数に相関はなくなるはずです。
11.6 発展的問題
11.6.1 スキルと給与の関係
ある企業の従業員データには、個人ごとの「スキル」「給与」「勤続年数」「年齢」の値が記録されています。このデータを使い、「スキルの高さは給与に反映されているか?」 を分析したいと考えました。
以下のコードを実行して、分析用のダミーデータを生成してから、問いに答えてください。
# データの生成(このまま実行してください)
library(tidyverse)
library(correlation)
library(see)
library(ggpubr)
set.seed(999)
n = 300
Age = rnorm(n, 40, 10)
Exp = 0.8 * Age + rnorm(n, 0, 5)
Skill = 0.7 * Exp + rnorm(n, 0, 10)
Salary = 0.6 * Exp + 0.3 * Age + rnorm(n, 0, 5)
dat_hr = data.frame(Age, Exp, Skill, Salary)問題:
- 通常の相関分析を行い、スキルと給与の関係を評価してください。
- 次に、偏相関分析を行い、同様に可視化も行ってください。
- 相関係数や偏相関係数の可視化(ヒートマップやネットワーク図)をしてください。
- これらに基づいて、スキルと給与に関係性についてどのような結論が導き出せますか?
ヒント:相関と偏相関の図を比較する際に、色の付き方を両方の図で揃える必要があります。
- ヒートマップでスケールの調整をするには scale_fill_gradient2() 関数を使います。
- ネットワーク図でスケールの調整をするには scale_edge_color_gradient2() 関数を使います。
解答と解説を表示
library(patchwork) # 図の結合
# 通常の相関
correlation(dat_hr)
## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(298) | p
## ------------------------------------------------------------------
## Age | Exp | 0.83 | [0.80, 0.87] | 26.16 | < .001***
## Age | Skill | 0.43 | [0.33, 0.52] | 8.25 | < .001***
## Age | Salary | 0.78 | [0.73, 0.82] | 21.64 | < .001***
## Exp | Skill | 0.51 | [0.42, 0.59] | 10.19 | < .001***
## Exp | Salary | 0.82 | [0.78, 0.86] | 25.16 | < .001***
## Skill | Salary | 0.42 | [0.32, 0.51] | 8.04 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 300
# 偏相関
correlation(dat_hr, partial = TRUE)
## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(298) | p
## -----------------------------------------------------------------------
## Age | Exp | 0.52 | [ 0.43, 0.59] | 10.41 | < .001***
## Age | Skill | 0.01 | [-0.10, 0.13] | 0.23 | > .999
## Age | Salary | 0.30 | [ 0.19, 0.40] | 5.43 | < .001***
## Exp | Skill | 0.26 | [ 0.15, 0.36] | 4.65 | < .001***
## Exp | Salary | 0.48 | [ 0.39, 0.57] | 9.53 | < .001***
## Skill | Salary | 2.27e-03 | [-0.11, 0.12] | 0.04 | > .999
##
## p-value adjustment method: Holm (1979)
## Observations: 300
# ヒートマップに共通のスケール設定
common_fill_scale = scale_fill_gradient2(
low = "red", mid = "white", high = "steelblue",
midpoint = 0, limit = c(-1, 1), name = "r"
)
# 通常の相関ヒートマップ
p_heat1 = correlation(dat_hr) %>%
summary(redundant = TRUE) %>%
plot(type = "tile", show_values = TRUE, digits = 2) +
common_fill_scale +
coord_fixed() + # セルを正方形にする
labs(title = "通常相関")
# 偏相関ヒートマップ
p_heat2 = correlation(dat_hr, partial = TRUE) %>%
summary(redundant = TRUE) %>%
plot(type = "tile", show_values = TRUE, digits = 2) +
common_fill_scale +
coord_fixed() +
labs(title = "偏相関")
# patchworkを使って結合
p_heat1 + p_heat2 +
plot_layout(guides = "collect") # 凡例をひとつにまとめる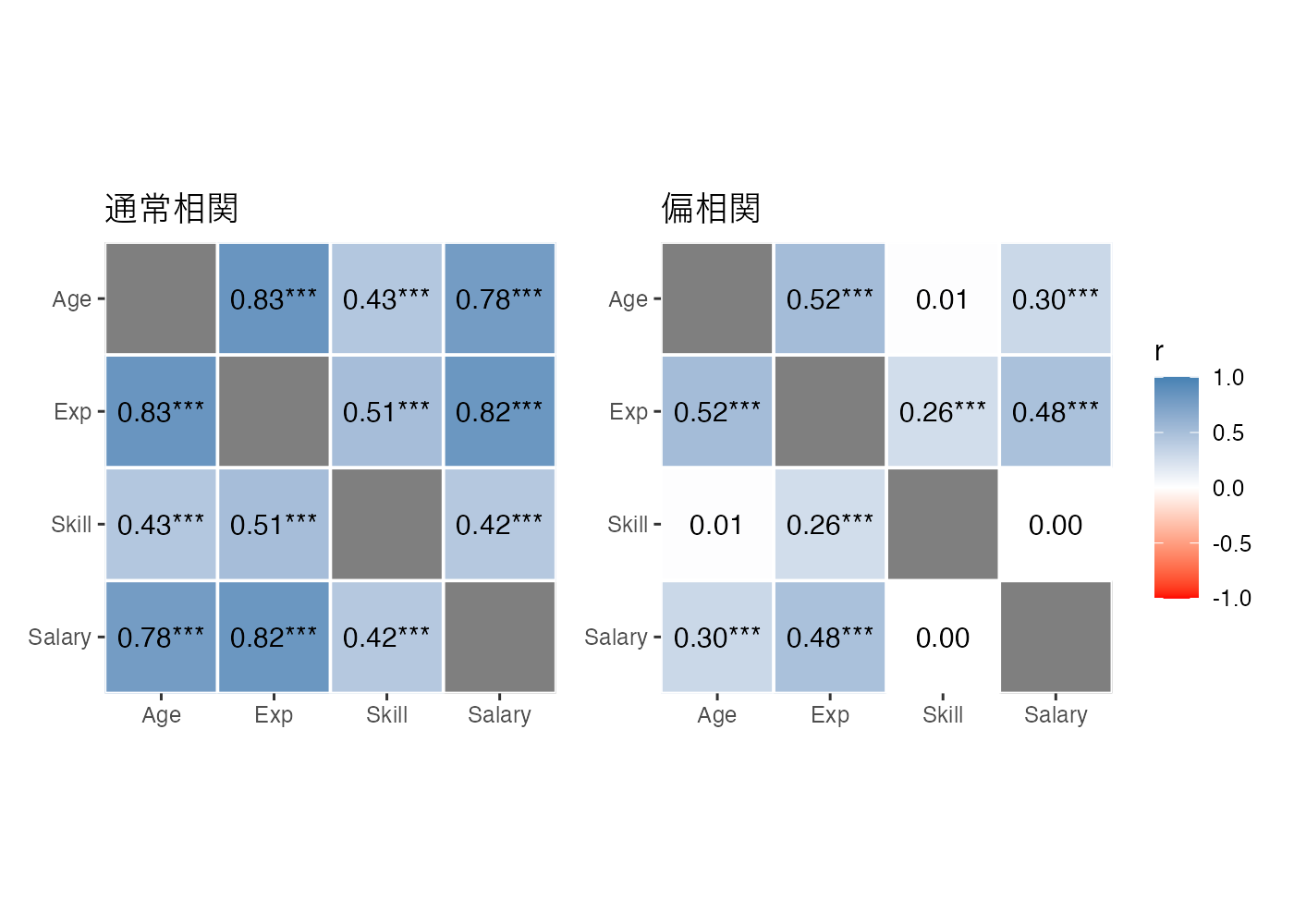
# ネットワーク図にに共通のスケール設定
common_scale = scale_edge_color_gradient2(
low = "red", mid = "white", high = "steelblue",
midpoint = 0, limit = c(-1, 1), name = "r"
)
# 通常の相関ネットワーク
p_net1 = correlation(dat_hr) %>%
plot(show_data = "points") +
common_scale +
labs(title = "通常の相関係数", subtitle = "すべてが繋がって見える")
# 偏相関ネットワーク
p_net2 = correlation(dat_hr, partial = TRUE) %>%
plot(show_data = "points") +
common_scale +
labs(title = "偏相関係数", subtitle = "スキルと給与の線が消失")
# patchworkを使って結合
p_net1 + p_net2 +
plot_layout(guides = "collect")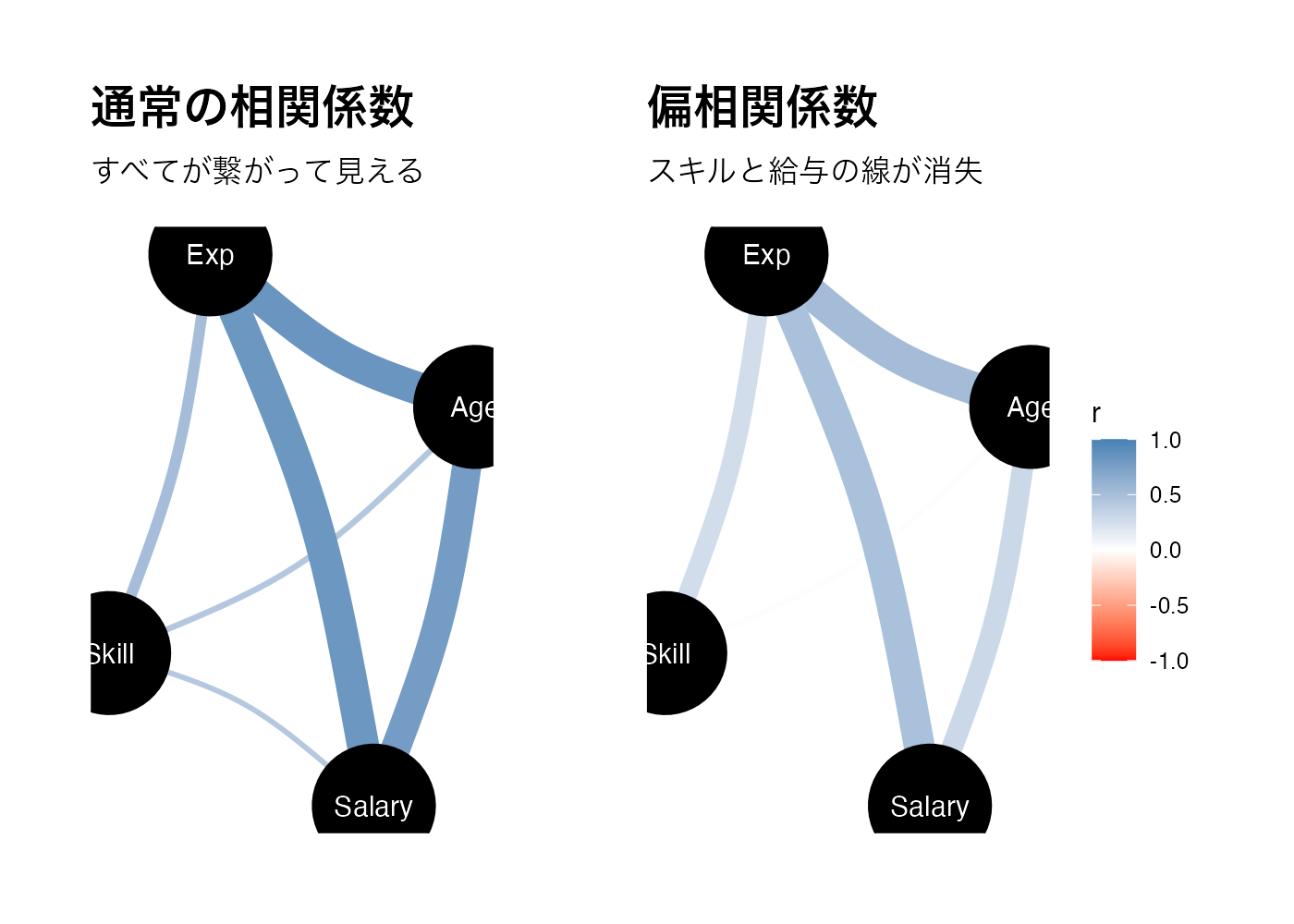
通常の相関ではスキルと給与の間に有意な正の相関(r = .42)が見られます。しかし、偏相関を使い、年齢や経験の影響を統制した場合、その相関はほぼ0になりました。
一見するとスキルが高いほど給与も高いように見えるが、それは単に「ベテラン(高齢・経験豊富)だからスキルも給与も高いだけ」という見かけ上の関連である。年齢と経験の影響を取り除くと、スキルそのものは給与にほとんど直接的な影響を与えていないと考えられます。
作図上のポイントとして、複数の図を比較する際は、limit = c(-1, 1) などでスケールを統一し、相関係数の値と色のつき方を揃える必要があります。これが揃っていないと、図を誤って解釈してしまいやすくなります。