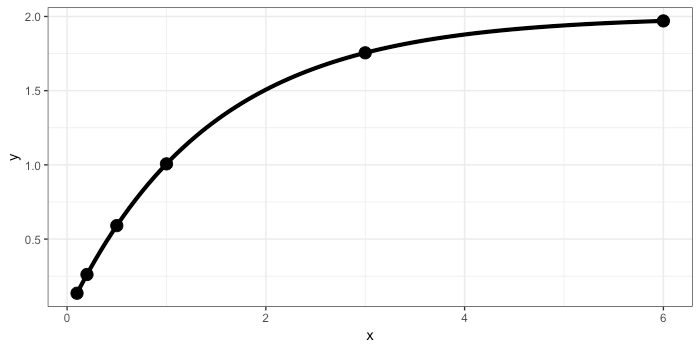
データがある曲線 y = a * ( 1 - exp( -b * t ) ) に従っているとします。 a と b は関数のパラメータです。 例えば a = 2, b = 0.7 の場合には、この曲線は次のようになります。
library( ggplot2 )
library( ggthemes )
# 曲線の関数
mycurve = function( x, a, b ){
return( a * ( 1 - exp( -b * x ) ) )
}
# データの作成
a = 2
b = .7
mydata = data.frame(
x = c ( 0.1, 0.2, 0.5, 1, 3, 6 ),
y = mycurve( c( 0.1, 0.2, 0.5, 1, 3, 6 ), a, b )
)
p = ggplot( mydata, aes( x = x, y = y ) ) +
stat_function( fun = mycurve, args = list( a = a, b = b ), size = 1.5 ) +
geom_point( size = 4 ) +
theme_bw()
plot( p )
optim関数によるパラメータ推定
次に、この関数に従っていると想定されるデータがある時に、関数のパラメータを推定します。 推定には optim 関数を使用します。 optim 関数には推定したいパラメータの初期値と、最小化したい関数を指定します。 最小二乗法を使う場合は、最小化したい関数は二乗誤差になります。 以下の例では最小化したい関数を errorfn という名前の関数で作成しています。
library( ggplot2 )
library( ggthemes )
# 曲線の関数
mycurve = function( x, a, b ){
return( a * ( 1 - exp( -b * x ) ) )
}
# データの作成
a = 2
b = .7
mydata = data.frame(
x = c (0.1, 0.2, 0.5, 1, 3, 6 ),
y = mycurve( c(0.1, 0.2, 0.5, 1, 3, 6 ), a, b )
)
# データにノイズを加える
mydata$y = mydata$y + rnorm( 6, mean = 0, sd = .1 )
# 最小二乗法によるパラメータの推定( p はパラメータ、d はデータです)
errorfn = function( p, d ) {
y = sum( ( mycurve( d$x, p[ 1 ], p[ 2 ]) - d$y )^2 )
}
params = optim( par = c( 1, 1 ), fn = errorfn, d = mydata )$par
# par は推定したいパラメータの初期値で、適当な値を指定します(ここでは a と b の両方とも1)
# fn は最小化したい関数で、この関数の引数 d に mydata を指定しています
print( params )
# 結果の図示
p = ggplot( mydata, aes( x = x, y = y ) ) +
stat_function( fun = mycurve, args = list( a = a, b = b ), size = 1.5 ) +
stat_function( fun = mycurve, args = list( a = params[1], b = params[2] ), color = "red", size = 1.5 ) +
geom_point( size = 4 ) +
theme_bw()
plot( p )
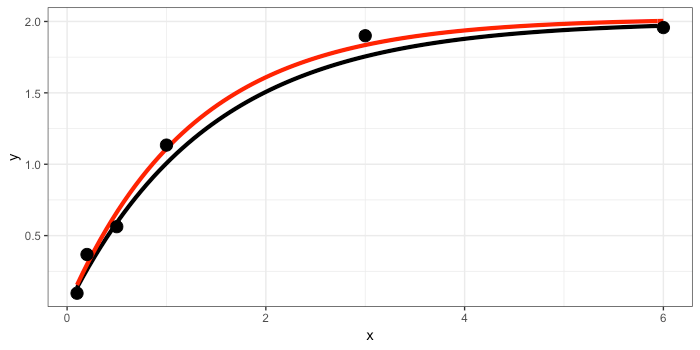
params という変数にパラメータの推定結果が入っています。 a = 2.0209496, b = 0.795333 という結果が得られました。 a = 2, b = 0.7 が正解なので、近い値が出ています。 (データにノイズを加えずにやればほぼ正解と同じ値になります) 赤線は推定されたパラメータを使って引いた(データにフィットさせた)曲線です。 黒線はノイズを含まない場合の曲線(真のモデル)です。

コメント